R त्रिज्या की एक वृत्ताकार वलय, जिसकी प्रति एकांक लम्बाई पर एकसमान धन आवेश λ है। तल में स्थित है तथा इसका केंद्र मूल बिंदु O पर है एक कण जिसका द्रव्यमान m है तथा जिस पर धन-आवेश q है, धन x-अक्ष पर स्थित बिन्दु P (R sqrt3, 0, 0) से सीधे O की ओर प्रारम्भिक वेग v से प्रक्षेपित किया जाता है। v का वह न्यूनतम (अशून्य) मान ज्ञात कीजिए जिससे कि कण बिन्दु P पर वापिस नहीं लौटे।
The correct Answer is:Vmin=√gλ2ε0m
CB=Kε0Ad=(9)(8.85×10−12)(0.02)(8.85×10−4)
=1.8×10−9फेरेड
CA तथा CB समांतर क्रम में है, अंत: निकाय की कुल धारिता,
C=C′A+CB=(0.4+1.8)×10−9
=2.2×10−9 फेरेड
निकाय में सचित आवेश q=qA=2.2×107 कुलाम
सचित ऊर्जा U=12q2C=12(2.2×10−7)2(2.2×10−9)
या U=1.1×10−5 जूल
वाले में कुल आवेश Q=(2πR)λ
वाले के केंद्र से उसकी अक्ष पर x दुरी पर विभव
V(x)=14πε0.Q√R2+x2
तथा केंद्र पर Vकेंद्र=14πε0QR
उपरोक्त सूत्रो से VP=14πε0.2πRλ√R2+3R2=λ4ε0
VO=14πε0.2πRλR=λ2peis0
स्पष्तः VO>VP
O तथा P के बिच विभान्तर
V=VO−VP
=λ2ε0−λ4πε0=λ4ε0
∴12mv2≥qV
⇒v≥√2qVm
या v≥√(qλ)2ε0m)
∴vmin=√qλ2ε0m
Topper's Solved these Questions
- BOOK - JEE Main & Advanced (Hindi Medium)CHAPTER - स्थिर वैघुतिकीEXERCISE - श्रृंखलाबद्ध-बोधन प्रकार3videos
स्थिर वैघुतिकी
- BOOK - JEE Main & Advanced (Hindi Medium)CHAPTER - स्थिर वैघुतिकीEXERCISE - एकल पूर्णांक उत्तर प्रकार4videos
स्थिर वैघुतिकी
- BOOK - JEE Main & Advanced (Hindi Medium)CHAPTER - सॉल्व्ड पेपर 2017 JEE ADVANCEDEXERCISE - पेपर 2(खण्ड-3)4videos
सॉल्व्ड पेपर 2017 JEE ADVANCED
Similar Questions
नाभिकीय आवेश (Ze), R त्रिज्या वाले नाभिक के भीतर असमान रूप से वितरित रहता हैं। आवेश घनत्व p(r) (अर्थात् एकांक आयतन में आवेश की मात्रा) नाभिक के केन्द्र से त्रिज्य दूरी (r) पर ही निर्भर करता है। वैद्युत क्षेत्र त्रिज्य दिशा के अनुदिश है।
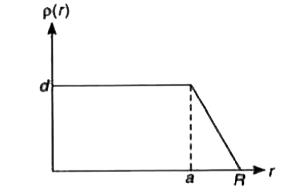
दूरी r= R पर वैघुत क्षेत्र है।04:29View Solutionत्रिज्या R के एक ठोस गोले के सम्पूर्ण आयतन में आवेश Q को इस प्रकार बाँटा गया है कि आवेश-घनत्व p=kra है। यहाँ k तथा a व नियतांक हैं तथा r गोले के केन्द्र से दूरी है। यदि इस गोले में r=R2 पर विद्युत का मान r= R पर विद्युत क्षेत्र के मान का 18 है, तो नियतांक a का मान निकालें।
03:29View Solutionएक साधारण RC परिपथ को देखिए, जैसा चित्र 1 (Figure 1) में दर्शाया गया है। प्रक्रम 1 (Process1) t= 0 पर स्विच S द्वारा परिपथ पूर्ण किया जाता है एवं संधारित्र पूर्ण रूप से वोल्टता V0 से आवेशित हो जाता है। (T» RC समय तक आवेषण चलता रहता है। इस प्रक्रम में प्रतिरोध के द्वारा कुछ विद्युत-कर्जा क्षय (energy dissipated) ED होती है। पूर्ण रूप से आवेशित संधारित्र में संचित ऊर्जा (stored energy in a charged capacitor) का मान EC है।
Q प्रक्रम 1, में संधारित्र में संचित ऊर्जा EC और प्रतिरोध R द्वारा ऊर्जा क्षय E0में सम्बनध है।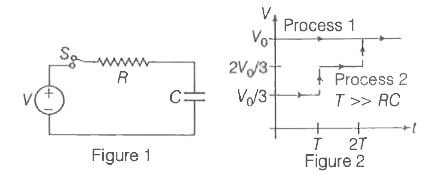
04:21View Solutionपरवलय y2=4ax की नाभि तथा उस पर स्थित चर को मिलाने वाले रेखाखण्ड के मध्य - बिंदु का पथ एक परवलय है जिसकी नियता है :
08:00View Solutionएक रेखा X- अक्ष तथा Y-अक्ष को बिंदु A तथा B पर मिलती है AB का मध्य बिंदु (x1,y1) है तो रेखा का समीकरण है -
03:14View Solutionएक छड़ की लम्बाई l है । इसका एक सिरा भूमि पर तथा दूसरा सिरा एक ऊर्ध्वाधर दीवार पर टिका है । यदि छड़ भूमि पर फिसले , तो उसके मध्य बिंदु का बिन्दुपथ ज्ञात कीजिए ।
04:14View Solutionएक अतिपरवलय बिन्दु P(√2,√3) से होकर जाता है, तथा उसकी नाभियाँ (±2,0) पर है, तो अतिपरवलय के बिन्दु P पर खींची गई स्पर्श रेखा जिस बिन्दु से होकर जाती है, वह है
02:29View Solutionयदि एक दीर्घवृत्त जिसका केंद्र मूलबिंदु पर है, के दीर्घ कक्ष तथा लघु कक्ष कि लम्बाइयों का अंतर 10 है तथा एक नाभिकेन्द्र (0,5√3) पर है, तो इसके नाभिलम्ब की लम्बाई है
04:26View Solutionरेखा 4x−3y+2=0 के समांतर रेखाएं खींची गई है जो मूलबिंदु 35 से की दुरी पर है, तो निम्न में से कौन-सा एक बिंदु इनमे से किसी रेखा पर स्थित है?
04:06View Solutionएक अतिपरवलय का केंद्र मूलबिंदु पर है तथा यह बिन्दु (4,2) से होकर जाता है और इसका अनुप्रस्थ (transverse) अक्ष X-अक्ष के अनुदिश है जिसकी लम्बाई 4 है तो इस अतिपरवलय की उत्केन्द्रता (eccentricity) है
04:29View Solutionएक वृत्त X-अक्ष पर एक जीवा काटता है जिसकी लम्बाई 4a है तथा यह वृत्त Y-अक्ष के एक बिन्दु से होकर जाता है जिसकी मूलबिंदु से दुरी 2b है , तो वृत्त के केन्द्र का बिन्दुपथ (locus) है
05:40View Solutionमाना एक दीर्घवृत्त जिसका दीर्घ -अक्ष, X-अक्ष के अनुदिश है तथा केन्द्र मूलबिंदु पर है, के नाभिलम्ब की लम्बाई 8 है । यदि दीर्घवृत्त की नाभियो के बीच की दुरी, इसके लघु-अक्ष की लम्बाई के समान हो, तो निम्न में से कौन-सा बिन्दु इस पर स्थित है?
06:39View Solutionयदि एक अतिपरवलय के शीर्ष (−2,0) तथा (2,0) पर है तथा इसकी एक नाभि (−3,0) पर है, तो निम्न में से कौन-सा बिन्दु इस अतिपरवलय पर स्थित नहीं है
02:42View Solutionयदि एक वक्र बिंदु (1, -2) से होकर जाता है तथा इस पर किसी बिंदु (x, y) पर स्पर्श रेखा का ढाल (slope) x2−2yx है, तो यह वक्र निम्न में से किस बिंदु से होकर जाता है ?
01:50View Solutionयदि R त्रिज्या का एक वृत्त मूलबिंदु O से होकर जाता है तथा निर्देशांक अक्षो को A और B पर कट्टा है , तो O से रेखा AB पर डाले गए लम्ब के पाद का बिन्दुपथ है
04:14View Solution