r त्रिज्या का एक चालक गोला S1 विघुतरोगी हैण्डिल से सम्बन्ध है एक दूसरा चालक गोला S2, जिसकी त्रिज्या R है एक विघुतरोगी स्टैण्ड पर ज्यादा है गोला S2 प्रारंभ में अनाववेशित है गोले S1 को Q आवेश दिया जाता है उसे S2 के संपर्क में लाया जाता है तथा फिर हटा लिया जाता है S2 को पुनः आवेशी किया जाता है जिससे की उस पर पुनः Q आवेश हो जाता है पुनः इसको S2 के संपर्क में लाया जाता है तथा हटा लिया जाता है यही क्रिया बार n दोहराई जाती है
(a) S1 के साथ इस प्रकार के n सम्पर्कों के पश्चात् S2 की स्थिरवैद्युत ऊर्जा ज्ञात कीजिए
(b) इस ऊर्जा का सीमान्त मान क्या होगा, यदि n→∞
The correct Answer is:Un=q2n8πε0R (b) U∞=Q2R8πε0r2
जहाँ qn=QRr[1−(RR+r)n]
गोलीय चालकों की धारितायें उनकी त्रिज्याओं के अनुपात में होती हैं। माना S1 तथा S2 की धारितायें C1 व C2 हैं तब C2C1=Rr
(a) आवेशो का वितरण धारिताओं के अनुपात में होगा। माना पहले सम्पर्क में S2 द्वारा प्राप्त आवेश, q1 अत: S1 पर आवेश Q−q1(=q1') होगा∣∣
∴q1q2=q1Q−q1=C2C1=Rr
∴q1=Q(RR+r).......(i)
दूसरे संपर्क में S1 पुनः उसी अनुपात में वितरित होगा, अंत: S1 व् S2पर कुल आवेश
Q+q1=Q(1+RR+r)
यह आवेश पुनः उसी अनुपात में वितरित होगा, अंत: दूसरे संपर्क में S2 पर आवेश
q2=Q(1+RR+r)(RR+r)=Q[RR+r+(RR+r)2]
इसी प्रकार
q3=Q[RR+r+(RR+r)2+(RR+r)3]
तथा qn=Q[RR+r+(RR+r)2+.....+(RR+r)n]
या qn=QRr[1−(RR+r)n)].........(i) [Sn=(a1−rn(1−r)के प्रयोग से]
n सम्पर्को के बाद की स्थिर वैघुत ऊर्जा
Un=q2n2C=q2n2(4πε0R) या Un=q2n8πε0R
जहाँ qn का मान समी (i) से लिखा जा सकता है
चुकी n→∞
q∞=QRr
∴U∞=q2∞2C=Q2R2/r28πε0R
या U∞=Q2R8πε0r2
Topper's Solved these Questions
- स्थिर वैघुतिकीBOOK - JEE Main & Advanced (Hindi Medium)CHAPTER - स्थिर वैघुतिकीEXERCISE - श्रृंखलाबद्ध-बोधन प्रकार
3 Videos
- स्थिर वैघुतिकीBOOK - JEE Main & Advanced (Hindi Medium)CHAPTER - स्थिर वैघुतिकीEXERCISE - एकल पूर्णांक उत्तर प्रकार
4 Videos
- सॉल्व्ड पेपर 2017 JEE ADVANCEDBOOK - JEE Main & Advanced (Hindi Medium)CHAPTER - सॉल्व्ड पेपर 2017 JEE ADVANCEDEXERCISE - पेपर 2(खण्ड-3)
4 Videos
Similar Questions
नाभिकीय आवेश (Ze), R त्रिज्या वाले नाभिक के भीतर असमान रूप से वितरित रहता हैं। आवेश घनत्व p(r) (अर्थात् एकांक आयतन में आवेश की मात्रा) नाभिक के केन्द्र से त्रिज्य दूरी (r) पर ही निर्भर करता है। वैद्युत क्षेत्र त्रिज्य दिशा के अनुदिश है।
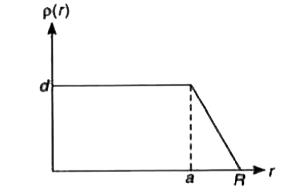
दूरी r= R पर वैघुत क्षेत्र है।
View Solutionत्रिज्या R के एक ठोस गोले के सम्पूर्ण आयतन में आवेश Q को इस प्रकार बाँटा गया है कि आवेश-घनत्व p=kra है। यहाँ k तथा a व नियतांक हैं तथा r गोले के केन्द्र से दूरी है। यदि इस गोले में r=R2 पर विद्युत का मान r= R पर विद्युत क्षेत्र के मान का 18 है, तो नियतांक a का मान निकालें।
View Solutionएक साधारण RC परिपथ को देखिए, जैसा चित्र 1 (Figure 1) में दर्शाया गया है। प्रक्रम 1 (Process1) t= 0 पर स्विच S द्वारा परिपथ पूर्ण किया जाता है एवं संधारित्र पूर्ण रूप से वोल्टता V0 से आवेशित हो जाता है। (T» RC समय तक आवेषण चलता रहता है। इस प्रक्रम में प्रतिरोध के द्वारा कुछ विद्युत-कर्जा क्षय (energy dissipated) ED होती है। पूर्ण रूप से आवेशित संधारित्र में संचित ऊर्जा (stored energy in a charged capacitor) का मान EC है।
Q प्रक्रम 1, में संधारित्र में संचित ऊर्जा EC और प्रतिरोध R द्वारा ऊर्जा क्षय E0में सम्बनध है।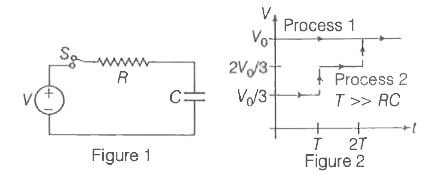
View Solutionदो विधुतरूधर ताँबे के समरूप आवेशित गोलों A और B में क्रमश: qA और qB आवेश है। उसी साइज का तीसरा अनावेशित गोला C पहले गोले A के संपर्क में रखा जाता है। तथा उसके बाद गोले B के संपर्क में रखा जाता है। अंत में दोनों से दूर कर दिया जाता है। A और B में नए आवेश क्या होंगे ?
View Solutionएक वृत्त X-अक्ष पर एक जीवा काटता है जिसकी लम्बाई 4a है तथा यह वृत्त Y-अक्ष के एक बिन्दु से होकर जाता है जिसकी मूलबिंदु से दुरी 2b है , तो वृत्त के केन्द्र का बिन्दुपथ (locus) है
View Solutionमाना Sk=1+2+3+…+kk है। यदि S21+S22+….S210=512A है, तो A बराबर है
View Solutionयदि एक वक्र बिंदु (1, -2) से होकर जाता है तथा इस पर किसी बिंदु (x, y) पर स्पर्श रेखा का ढाल (slope) x2−2yx है, तो यह वक्र निम्न में से किस बिंदु से होकर जाता है ?
View Solutionयदि R त्रिज्या का एक वृत्त मूलबिंदु O से होकर जाता है तथा निर्देशांक अक्षो को A और B पर कट्टा है , तो O से रेखा AB पर डाले गए लम्ब के पाद का बिन्दुपथ है
View Solutionएक बंद पात्र में 25^(@)C पर साम्यावस्था SO_(2)CI_(2)(g) को प्राप्त किया जाता है और एक अक्रिय गैस, हीलियम को प्रवेशित किया जाता है । निम्नलिखित में से कौन सा कथन सही है ?
View Solutionजब धातु M को NaOH के साथ उपचारित किया जाता है, तो एक श्वेत जिलेटिन जैसा अवक्षेप 'X' प्राप्त होता है, जो NaOH के आधिक्य में घुलनशील होता है। यौगिक 'X' प्रबल रूप से गर्म करने पर एक ऑक्साइड देता है जिसका उपयोग वर्णलेखिकी में एक अधिशोषक के रूप में किया जाता है। धातु 'M' है:
View Solutionएक यौगिक (A) का उपयोग सॉल्वे प्रक्रम में अमोनिया की पुनः प्राप्ति के लिए धावन सोडा के विचरन में किया जाता है। जब CO_(2) को (A) के जलीय विखंडन में बुदबुदाया जाता है तो विलयन दूधिया हो जाता है। इसका उपयोग विसंक्रामक प्रकृति के कारण सफेदी में किया जाता है। A का रासायनिक सूत्र क्या होगा?
View SolutionNaCl के संकुलन प्रभाज के लिए निम्नलिखित में से कौन सा व्यंजक सही है, यदि एक फलक और एक विकर्ण से a- आयन को हटा दिया जाता है?
View Solutionएक दवा तैयार करने के लिए निम्नलिखित में से किसका उपयोग किया जाता है, जिसका उपयोग एक महत्वपूर्ण विस्फोटक, RDX बनाने में भी किया जाता है?
View Solutionएक आदर्श गैस को ABCA चक्रीय प्रक्रम में निम्नानुसार लिया जाता है, तो गैस द्वारा किया गया कार्य है:
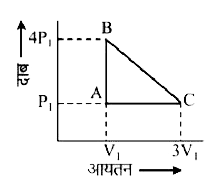
View Solutionएक यौगिक A का अणु सूत्र C_(2)Cl_(3)OH है। यह फेहलिंग विलयन को अपचयित करता है और ऑक्सीकरण पर एक मोनोकार्बोक्सिलिक अम्ल (B) देता है। एथिल ऐल्कोहॉल पर क्लोरीन की क्रिया द्वारा A प्राप्त किया जाता है। A है:
View Solutionएक साइक्लोहेक्सेनोन, अम्ल उत्प्रेरक मात्रा की उपस्थिति में डाइमेथिलएमीन के साथ अभिक्रिया पर एक यौगिक का निर्माण करता है, यदि अभिक्रिया के दौरान जल का लगातार निष्कासन किया जाता है, तब निर्मित यौगिक को सामान्यतः जाना जाता है
View Solution
