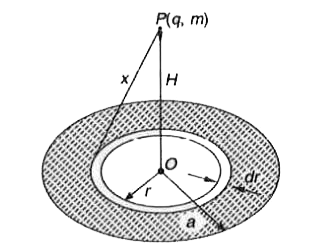
एक कुचालक चकती जिसकी त्रिज्या a एवं समरूप क्षेत्रिय आवेश घनत्व σ है, को जमीन पर रखा गया है इसके केन्द्र से गुजरने वाला अक्ष उर्ध्वाधर है| m द्रव्यमान एवं q आवेश का कण अक्ष के अनुदिश H ऊँचाई से शून्य प्रारम्भिक वेग से छोडा गया। कण के लिये qm=4ε0gσ
(a) यदि कण चकती तक पहुँच जाए इसके लिये H का मान ज्ञात करें।
(b) कण की स्थितिज ऊर्जा का ऊँचाई के साथ ग्राफ बनाये एवं साम्यावस्था की स्थिति ज्ञात करें।
The correct Answer is:(a) H=43a (b) H=a√3
डिस्क में निहित आवेश dq=(2πrdr)σ
डिस्क के कारण P पर विभव
dV=14πε0.dqx
जहाँ x=√H2+r2
dV=14πε0.(2πrdr)σ√H2+r2
=σ2ε0rdr√H2+r2
सम्पूर्ण डिस्क के कारण विभव VP∫r=ar=0dV=σ2ε0∫r=0r=0rdr√H2+r2
VP=σ2ε0[√a2+H2−H]
केंद्र O पर विभव VO=σa2ε0(H=0)
(a) कण P से छोड़ा गया है तथा यह बिंदु O पर पहुँचता है ऊर्जा संरक्षण के नियम से, गुरुत्वीय स्थितिज ऊर्जा में कमी =स्थिर वैघुत ऊर्जा में वृद्धि
⇒mgH=q(VO−VP)(△KE=0∴Ki=Kf=0)
या gH=(qm)(σ2ε0t−√a2+H2+H].....(i)
या qm=4πε0gσ
∴qσ2ε0m=2g
ययह मान समी (i) में रखने पर
gH=2g[a+H−√a2+H2]
या H2=(a+H)−√a2+H2
या a2+H2=a2+H24+aH
⇒H=43a तथा H=0
∴H=43a
(b) उचाई H पर कण की स्थितिज ऊर्जा =स्थिर वैघुत ऊर्जा +गुरुत्वीय स्थितिज ऊर्जा
U=qV=mgH
यहाँ V=H उचाई पर विभव
या U=σq2ε0[√a2+H2−H]+mgH....(ii)
समान्यवस्था में, F=−dUdH=0
समी (ii) से (अवकलन करने पर)
mg+σ2ε0[(12)(2H)1√a2+H2−1]=0(∴σq2peis0=2mg)
thererforemg+2mg[H√a2+H2−1=0
या 1+2H√a2+H2−2=0
या 2H√a2+H2=1⇒3H2=a2
या H=a√3
समी (ii) से,
U=mg(2√a2+H2−H)(परवलयाकार परिवर्तन)
U=2mga (H=0 पर)
तथा U=Umin=√3mga(H=a√3पर)
U-H ग्राफ चित्रानुसार होगा
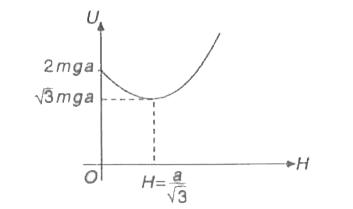
H=a√3 पर U न्यूनतम है
अंत: H=a√3 स्थायी सामान्यावस्था है
Topper's Solved these Questions
- BOOK - JEE Main & Advanced (Hindi Medium)CHAPTER - स्थिर वैघुतिकीEXERCISE - श्रृंखलाबद्ध-बोधन प्रकार3videos
स्थिर वैघुतिकी
- BOOK - JEE Main & Advanced (Hindi Medium)CHAPTER - स्थिर वैघुतिकीEXERCISE - एकल पूर्णांक उत्तर प्रकार4videos
स्थिर वैघुतिकी
- BOOK - JEE Main & Advanced (Hindi Medium)CHAPTER - सॉल्व्ड पेपर 2017 JEE ADVANCEDEXERCISE - पेपर 2(खण्ड-3)4videos
सॉल्व्ड पेपर 2017 JEE ADVANCED
Similar Questions
नाभिकीय आवेश (Ze), R त्रिज्या वाले नाभिक के भीतर असमान रूप से वितरित रहता हैं। आवेश घनत्व p(r) (अर्थात् एकांक आयतन में आवेश की मात्रा) नाभिक के केन्द्र से त्रिज्य दूरी (r) पर ही निर्भर करता है। वैद्युत क्षेत्र त्रिज्य दिशा के अनुदिश है।
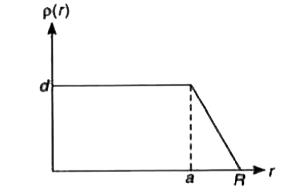
दूरी r= R पर वैघुत क्षेत्र है।09:03View Solutionत्रिज्या R के एक ठोस गोले के सम्पूर्ण आयतन में आवेश Q को इस प्रकार बाँटा गया है कि आवेश-घनत्व p=kra है। यहाँ k तथा a व नियतांक हैं तथा r गोले के केन्द्र से दूरी है। यदि इस गोले में r=R2 पर विद्युत का मान r= R पर विद्युत क्षेत्र के मान का 18 है, तो नियतांक a का मान निकालें।
04:52View Solutionएक साधारण RC परिपथ को देखिए, जैसा चित्र 1 (Figure 1) में दर्शाया गया है। प्रक्रम 1 (Process1) t= 0 पर स्विच S द्वारा परिपथ पूर्ण किया जाता है एवं संधारित्र पूर्ण रूप से वोल्टता V0 से आवेशित हो जाता है। (T» RC समय तक आवेषण चलता रहता है। इस प्रक्रम में प्रतिरोध के द्वारा कुछ विद्युत-कर्जा क्षय (energy dissipated) ED होती है। पूर्ण रूप से आवेशित संधारित्र में संचित ऊर्जा (stored energy in a charged capacitor) का मान EC है।
Q प्रक्रम 1, में संधारित्र में संचित ऊर्जा EC और प्रतिरोध R द्वारा ऊर्जा क्षय E0में सम्बनध है।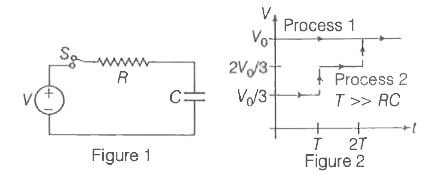
04:10View Solutionएकसमान विद्युत क्षेत्र E=3×103ˆi(N)/C पर विचार कीजिये ।
(a) इस क्षेत्र का 10 cm भुजा के वर्ग के उस पार्श्व से जिसका तल yz तल के समांतर है, गुजरने वाला फ्लक्स क्या है ?
(b) इस वर्ग से गुजरने वाला फ्लक्स कितना है यदि इसके तल का अभिलंब x- अक्ष से 60∘ कोण बनता है ?02:06View Solutionकिसी बिंदु आवेश के कारण उस बिंदु को केंद्र मानकर खींचे गए 10cm त्रिज्या के गोलीय गॉऊसीय पृष्ठ पर विद्युत से फ्लक्स −1.0×103Nm2/C त्रिज्या के गोलीय गॉऊसीय पृष्ठ पर विद्युत से फ्लक्स। (a) यदि गॉऊसीय पृष्ठ की त्रिज्या दो गुनी कर दी जाए तो पृष्ठ से कितना फ्लक्स गुजरेंगा ? (b) बिंदु आवेश का मान क्या है।
02:05View Solutionद्रव्यमान m के एक कण को गति y=ut+12gt2 से वर्णित है । उस कण पर लगने वाले बल को ज्ञात करो ।
04:45View Solutionउस बिंदु का बिन्दुपथ ज्ञात कीजिए
जिसकी x-अक्ष से दूरी उसकी y-अक्ष से दूरी की तीन गुनी है ।02:29View Solutionएक कण y=x2+2x से साथ-साथ चलता है। व्रक के किस बिंदु पर x तथा y निर्देशांक समान दर से परिवर्तित हो रहे है ?
04:26View Solutionएक परवलय का अक्ष X-अक्ष के अनुदिश है। यदि इसके शीर्ष तथा नाम नाभि , X-अक्ष कि धनात्मक दिशा में मूलबिंदु से क्रमशः 2 तथा 4 कि दुरी पर हैं , तो इनमें से कौन - सा बिन्दु इस परवलय पर स्थित नहीं है ?
04:06View Solutionएक अतिपरवलय का केंद्र मूलबिंदु पर है तथा यह बिन्दु (4,2) से होकर जाता है और इसका अनुप्रस्थ (transverse) अक्ष X-अक्ष के अनुदिश है जिसकी लम्बाई 4 है तो इस अतिपरवलय की उत्केन्द्रता (eccentricity) है
06:27View Solutionएक वृत्त X-अक्ष पर एक जीवा काटता है जिसकी लम्बाई 4a है तथा यह वृत्त Y-अक्ष के एक बिन्दु से होकर जाता है जिसकी मूलबिंदु से दुरी 2b है , तो वृत्त के केन्द्र का बिन्दुपथ (locus) है
06:34View Solutionमाना एक दीर्घवृत्त जिसका दीर्घ -अक्ष, X-अक्ष के अनुदिश है तथा केन्द्र मूलबिंदु पर है, के नाभिलम्ब की लम्बाई 8 है । यदि दीर्घवृत्त की नाभियो के बीच की दुरी, इसके लघु-अक्ष की लम्बाई के समान हो, तो निम्न में से कौन-सा बिन्दु इस पर स्थित है?
02:42View Solutionउन रेखाओं का समीकरण जिन पर मूल बिन्दु से डाला गया। लम्ब x-अक्ष के साथ 30∘ का कोण बनाता है और उनसे तथा x-अक्ष से बने त्रिभुज का क्षेत्रफल 50√3 वर्ग इकाई हो, है
08:10View Solutionबिन्दु (1, 2) से दीर्घवृत्त 3x2+2y2=5 पर खींची गई स्पर्शी युग्मों के बीच का कण है
01:23:57View Solutionएक वस्तु जिसका द्रव्यमान m है विराम से h ऊँचाई से गुरुत्वीय त्वरण g के अन्तर्गत गिरती है तथा यह रेत में गहराई d तक धंसती है। रेत में फँसने के दौरान औसत मन्दन होगा
01:19:07View Solutionएक द्विध्रुव 10 सेमी लम्बा तथा आवेश 500μC से बना है। इसके अक्ष से 25 सेमी दूरी पर विद्युत क्षेत्र की तीव्रता होगी
View Solution