The volume of solid obtained by revolving the curve y=secx between x=π4.
A
2π(1−√3)
B
2π(1+√3)
C
π(1−√3)
D
2π√3+1.
Text Solution
The correct Answer is:D
|
Topper's Solved these Questions
- APPLICATIONS OF INTEGRATIONBOOK - PREMIERS PUBLISHERSCHAPTER - APPLICATIONS OF INTEGRATIONEXERCISE - Answer the following questions.
18 Videos
- APPLICATIONS OF INTEGRATIONBOOK - PREMIERS PUBLISHERSCHAPTER - APPLICATIONS OF INTEGRATIONEXERCISE - SOLUTION TO EXERCISES 9.10
20 Videos
- APPLICATIONS OF DIFFERENTIAL CALCULUSBOOK - PREMIERS PUBLISHERSCHAPTER - APPLICATIONS OF DIFFERENTIAL CALCULUSEXERCISE - Problems For Practice (Answer the following question)
39 Videos
- APPLICATIONS OF MATRICES AND DETERMINANTS BOOK - PREMIERS PUBLISHERSCHAPTER - APPLICATIONS OF MATRICES AND DETERMINANTS EXERCISE - PROBLEMS FOR PRACTICE (II. Answer the following)
15 Videos
Similar Questions
Knowledge Check
The volume of the solid obtained by revolving about y-axis the area enclosed between the ellipse x2+9y2=9 and the strangth line x+3y=3, in the first quadrant is
A3πB4πC6πD9πThe volume of the solid formed by rotating the area enclosed between the curve y2=4x,x=4 and x = 5 about X-axis is (in cubic units)
A18πB36πC9πD24πThe volume of the solid generated by the revolution of the curve y=a3a2+x2 about x-axis is :
A12π3a2Bπ3a2C12π2a3Dπ2a3
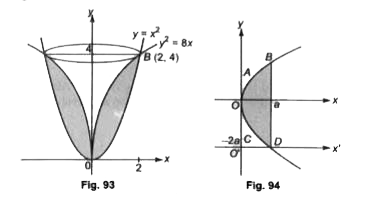
Compute the volume of the solid generated by revolving about the y-axis the figure bounded by the parabolas y=x2and8x=y2
View SolutionThe volume of the solid generated by the revolution of the curve y=a3a2+x2 about x-axis is :
View SolutionThe volume of solid generated by revolving about the y-axis the figure bounded by the parabola y=x2andx=y2 is
View SolutionThe volume of the solid formed by rotating the area between the curve y=x2 and the line y = 1 about y = 1 is (in cubic unit) :
View SolutionThe volume of the solid formed by rotating the area between the curve y=x2 and the line y = 1 about y = 1 is (in cubic unit) :
View Solution