A particle which is constrained to move along x - axis, is subjected to a force in the same direction which varies with the distance x of the particle from the origin as F(x)=kx+ax3. Here, k and a are positive constants. For x≥0, the functional form of the potential energy U (x) of the particle is Solution in Tamil
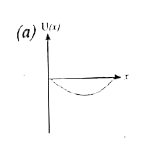
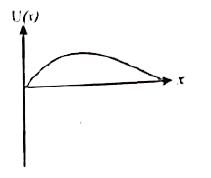
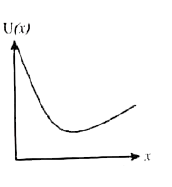
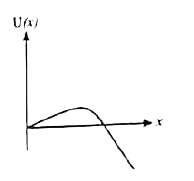
The correct Answer is:D
du=−f.dx
u=−x∫0(kx+ax3)dx
=kx22−ax44
When x=0,u=0
∴kx22=ax44
k=ax22
x=√2ka
Topper's Solved these Questions
- BOOK - PREMIERS PUBLISHERSCHAPTER - WORK, ENERGY AND POWER EXERCISE - SHORT ANSWER QUESTIONS42videos
WORK, ENERGY AND POWER
- BOOK - PREMIERS PUBLISHERSCHAPTER - WORK, ENERGY AND POWER EXERCISE - LONG ANSWER QUESTIONS38videos
WORK, ENERGY AND POWER
- BOOK - PREMIERS PUBLISHERSCHAPTER - WAVESEXERCISE - OTHER IMPORTANT & QUESTIONS ANSWERS ( NUMERICAL PROBLEMS. )48videos
WAVES
Similar Questions
Explain how the definition of work in physics is different from general perception.
04:19View SolutionExplain with graphs the difference between work done by a constant force and by a variable force.
05:56View SolutionThe equation of a wave is,
y(x,t)=0.05sin[π2(10x−40t)−π4]m Find,
The wavelength, the frequency and the wave velocity.
(ii) The particle velocity and acceleration at x=0.5 m and t=0.05 s.04:33View SolutionA particle which is constant to move along the x- axis , is subjected to a force in the same direction which varies with the distance x of the particle from the origin as F(x) = -Kx + ax^(3) . Hero K and a are positive constant . For x ge 0 , the fanctional from of the patential every U(x) of the particle is
01:42View SolutionA particle, which is constrained to move along x-axis, is subjected to a force in the some direction which varies with thedistance x of the particle from the origin an F (x) =-kx + ax^(3) . Here, k and a are positive constants. For x(ge0, the functional form of the potential energy (u) U of the U (x) the porticle is. (a) , (b) , (c) , (d) .
02:32View SolutionA particle, which is constrained to move along the x-axis, is subjected to a force from the origin as F(x) = -kx + ax^(3) . Here k and a are origin as F(x) = -kx + ax^(3) . Here k and a are positive constants. For x=0 , the functional form of the potential energy U(x) of particle is.
02:07View SolutionA particle constrained to move along the x-axis in a
potential V=kx2 is subjected to an external time dependent
force →f(t) here k is a constant, x the distance from the origin,
and t the time. At some time T, when the particle
has zero velocity at x = 0, the external force is removed.
Choose the incorrect options –
(1) Particle executes SHM
(2) Particle moves along +x direction
(3) Particle moves along – x direction
(4) Particle remains at rest02:07View Solutionएक कण पर, जो x - अक्ष पर चलने के लिए व्य्व्रुद्ध (constrained ) है, उसी दिशा में एक बल लगता है जिसका विचरण कण की मूलबिंदु से दुरी x के साथ फलन F(x)=−kx+ax3 के अनुसार है। यहाँ k तथा a धन नियतांक हैं। तब x≥0 के लिए कण की स्थितिज ऊर्जा U (x ) का सही फलन रूप है:
01:43View SolutionA particle which is constrained to move along x - axis, is subjected to a force in the same direction which varies with the distance x of the particle from the origin as F(x)=kx + ax^(3) . Here, k and a are positive constants. For x ge 0 , the functional form of the potential energy U (x) of the particle is
04:15View SolutionA particle which is constrained to move along x - axis, is subjected to a force in the same direction which varies with the distance x of the particle from the origin as F(x)=kx+ax3. Here, k and a are positive constants. For x≥0, the functional form of the potential energy U (x) of the particle is
View SolutionThe potential energy U(x) of a particle moving along x - axis is given by U(x)=ax-bx^(2) . Find the equilibrium position of particle.
02:07View Solutionएक कण मूल बिन्दु पर स्थित है और एक बल F=kx कण पर कार्यरत है (जहाँ, k एक धनात्मक नियतांक है।) यदि U(0)=0 हो, तो U(x) व X क मध्य आरेख होगा (जहाँ U फलन की ष्टिटीज ऊर्जा है)।
04:19View SolutionA particle, which is constrained to move along the x-axis, is subjected to a force in the same direction which varies with the distance of the particle from the origin as F(x) =-kx+ax^(3) . Hence k and a are positive constants. For 20. the functional form of the potential energy U(x) of the particle is:
03:40View SolutionA particle which is constrained to move along x - axis, is subjected to a force in the same direction which varies with the distance x of the particle from the origin as F(x)=kx+ax3. Here, k and a are positive constants. For x≥0, the functional form of the potential energy U (x) of the particle is
02:59View SolutionA particle which is constant to move along the x−aξs , is subjected to a force in the same direction which varies with the distance x of the particle from the origin as F(x)=−Kx+ax3 . Hero K and a are positive constant . For x≥0, the fanctional from of the patential every U(x) of the particle is
01:51View Solution
