A ball with a velocity of $5 m s^{- 1}$ impinges at angle of $60^{\circ}$ with the vertical on a smooth horizontal plane. If the coefficient of restitution is 0.5, find the velocity and direction after the impact. Solution in Tamil

Video Solution

Text Solution

Verified by Experts

$u = 5 m / s, θ = 60^{\circ}, e = 0.5, v = ? ?$

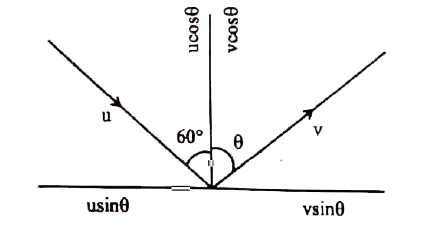
Formula:
$v cos θ = e u cos ϕ$
$v cos θ = e u {cos 60}^{\circ} ... (1)$
Horizontal comparison
$- v sin θ = u {sin 60}^{\circ} ... (2)$
${(1)}^{2} + {(2)}^{2}$ implies
$v^{2} [{sin}^{2} θ + {cos}^{2} θ] = e^{2} u^{2} {cos}^{2} 60^{\circ} + u^{2} {sin}^{2} 60^{\circ}$
$v^{2} = u^{2} (e^{2} {cos}^{2} 60^{\circ} + {sin}^{2} 60^{\circ})$
$v = u \sqrt{e^{2} {cos}^{2} 60^{\circ} + {sin}^{2} 60^{\circ}}$
$= 5 \sqrt{(\frac{1}{2}) . (\frac{1}{4}) + 3 / 4}$
$v = \frac{5}{2} \sqrt{3.25} \Rightarrow 4.5 m / s$
Substitute the value of v in eqn (1)
$4.5 cos θ = 0.5 \times 5 \times \frac{1}{2}$
$\frac{9}{2} cos θ = \frac{2.5}{2}$
$cos θ = \frac{2.5}{2} \times \frac{2}{9}$
$cos θ = 0.2778$
$= 73^{\circ} 54'$

Updated on:21/07/2023

|

Class 11 PHYSICS WORK, ENERGY AND POWER

Topper's Solved these Questions

Similar Questions

PREMIERS PUBLISHERS-WORK, ENERGY AND POWER -NUMERICAL PROBLEMS

Home
Ask Doubt
Profile