A block is performin SHM of amplitude 'A' in vertical direction. When block i8s at 'y' (measured from mean position), it detaches froms spring, so that spring contracts and does not effect the motion of the block. Find 'y⋅' such that block attains maximum height from the mean position. (given Aω2>g)
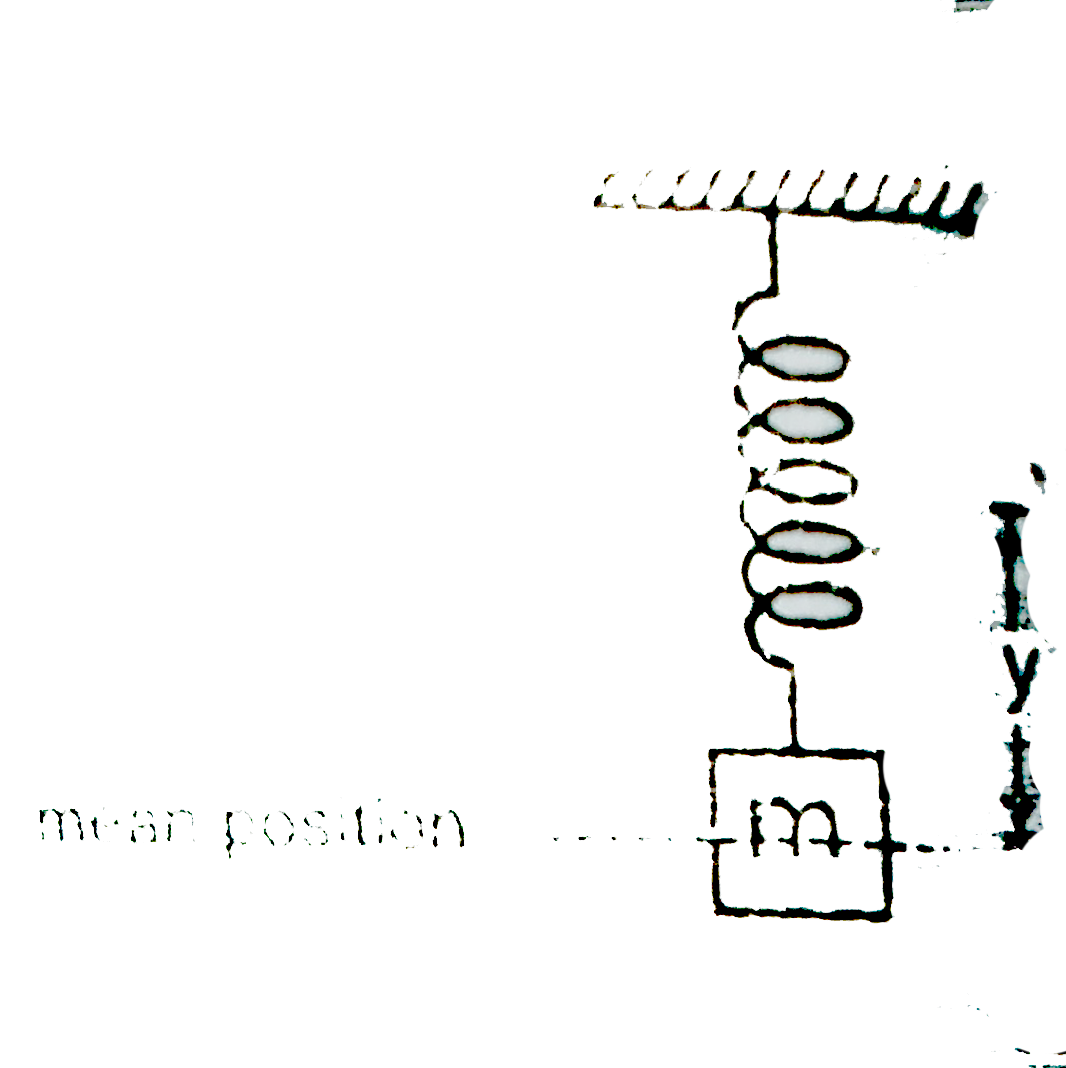
The correct Answer is:y∗=gω2
v2=ω2(A2−y2)……..(1)
h=v22g+y,h=ω2(A2−v2)2g+y
dhdy=0 (for maximum height)
dhdy=−ω22g(2y)+1=0⇒y∗=gω2
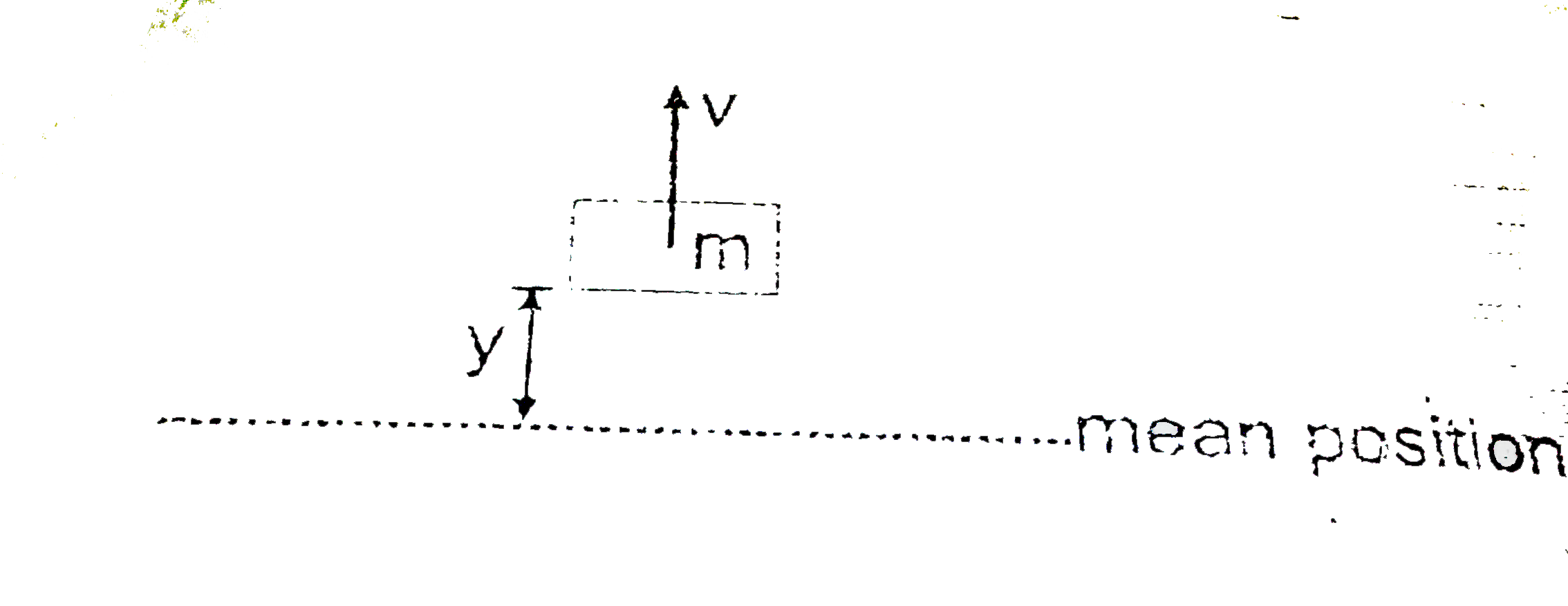
Topper's Solved these Questions
- BOOK - RESONANCECHAPTER - SIMPLE HARMONIC MOTION EXERCISE - Exercise- 3, PART - II17videos
SIMPLE HARMONIC MOTION
- BOOK - RESONANCECHAPTER - SIMPLE HARMONIC MOTION EXERCISE - Advanced Level Problems13videos
SIMPLE HARMONIC MOTION
- BOOK - RESONANCECHAPTER - SIMPLE HARMONIC MOTION EXERCISE - Exercise- 2, PART - IV8videos
SIMPLE HARMONIC MOTION
- BOOK - RESONANCECHAPTER - SEMICONDUCTORSEXERCISE - Exercise 388videos
SEMICONDUCTORS
- BOOK - RESONANCECHAPTER - TEST PAPERSEXERCISE - FST-330videos
TEST PAPERS
Similar Questions
A mass m is undergoing SHM in the verticl direction about the mean position y0 with amplitude A and anglular frequency ω. At a distance y form the mean position, the mass detached from the spring. Assume that th spring contracts and does not obstruct the motion of m. Find the distance y. (measured from the mean position). such that height h attained by the block is maximum (Aω2>g).
_E01_175_Q01.png) View Solution
View Solution
A block is released from height h, find the maximum compression of spring of spring constant k.View Solution
Knowledge Check
- Question 1 - Select One
A block of 200 g mass is dropped from a height of 2 m on to a spring and compress the spring to a distance of 50 cm. The force constant of the spring is
A20Nm−1B40Nm−1C30Nm−1D60Nm−1 - Question 2 - Select One
A particle suspended from a vertical spring oscillates 8 times per second. At the highest point of oscillation the spring becomes unstretched. The maximum speed of the block will be
A10 cm/sB20 cm/sC30 cm/sD40 cm/s - Question 3 - Select One
Find the maximum tension in the spring if initially spring at its natural length when block is released from rest.
 AmgBmg/2C3mg/2D2 mg
AmgBmg/2C3mg/2D2 mg
Block A of mass m is performing SHM of amplitude a. Another block B of mas m is gently placed on A when it passes through mean position and B sticks to A. Find the time period and amplitude of new SHM.
View SolutionA block of mass m suspended from a spring of spring constant k. Find the amplitude of S.H.M.
View SolutionA block in SHM starts from +A position. Write S−t equation of the block, if S is measured from −A.
View SolutionThe block is allwed to fall, slowly from the position wher spring is in its natural length. Find, maximum extension in the string.
 View Solution
View SolutionA block of mass m is released from a height h from the top of a smooth surface. There is an ideal spring of spring constant k at the bottom of the track. Find the maximum compression in the spring (Wedge is fixed)
 View Solution
View Solution

