Consider the equation where force, displacement, t time and = momentum. The dimensional formula of A will be
The correct Answer is:C
Appying dimensional analysis
Topper's Solved these Questions
- TEST PAPERSBOOK - BANSALCHAPTER - TEST PAPERSEXERCISE - PHYSICS PART (A)
32 Videos
- TEST PAPERSBOOK - BANSALCHAPTER - TEST PAPERSEXERCISE - PHYSICS PART (B)
3 Videos
- TEST PAPERSBOOK - BANSALCHAPTER - TEST PAPERSEXERCISE - PHYSICS PART- C
4 Videos
- SEMICONDUCTORSBOOK - BANSALCHAPTER - SEMICONDUCTORSEXERCISE - CBSE Question
32 Videos
Similar Questions
Knowledge Check
Consider the equation ddt(∫→F.d→S)=A(→F.→p) where →F≡ force, →s≡ displacement, t ≡ time and →p= momentum. The dimensional formila of A will be
AM0L0T0BML0T0CM−1L0T0DM0L0T−1Maxwell’s equation ∮→E.→dl=d→B.→Adt is a statement of-
AAmpere’s lawBFaraday’s law of inductionCGauss’s law of electricityDGauss’s law of magnetismif →P×→R=→Q×→R, then
A→P=→QB→P and →Q need not be equalCThere are infinite number of possibilities for →P (If →Q and →R are given ) which satisfy this relationship.D→p and →Q must be coplanar
Consider the following statements:
1. The magnitude of →a×→b is same as the area of a triangle with sides →aand→b.
2. If →a×→b=→0 where →a≠0.→b≠0 then →a=λ→b which of the following statements is/are correct?
View SolutionThe position of the particle is given by →r=(→i+2→j−→k) momentum →P=(3→i+4→j−2→k). The angular momentum is perpendicular to
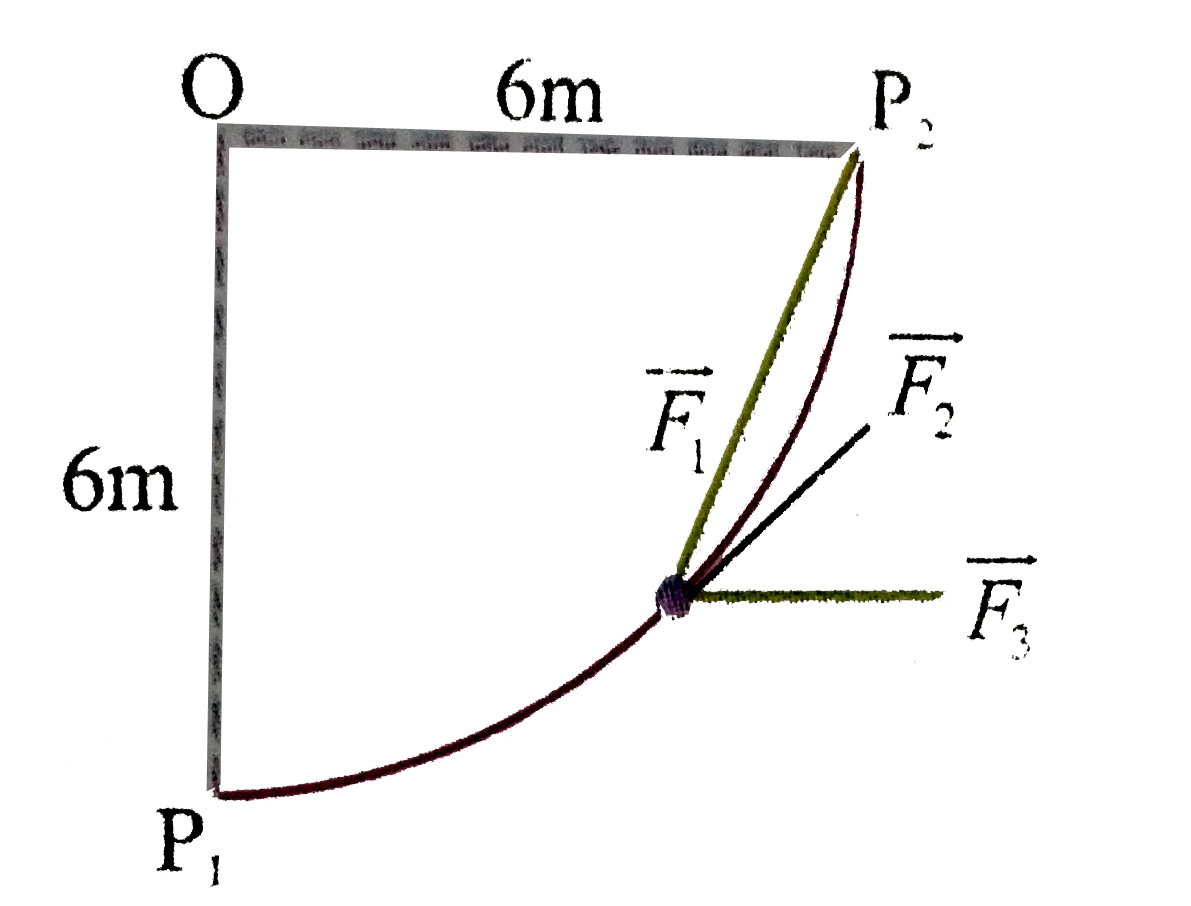
View SolutionA smooth track in the form of a quarter circle of radius 6m lies in the vertical plane. A particle moves from P1 to P2 under the action of forces →F1,→F2 and →F3 Force →F1 is 20N, Force →F2 is always 30N in magnitude. Force →F3 always acts tangentiallly to the track and is of magnitude 15N. Select the correct alternative (s) :
 .
.
View SolutionPoynting vectors →S is defined as →S=1μ0→E×→B. The average value of '→S' over a single period 'T' is given by
View SolutionConsider the following statements
1. For any three vectors →a→b→c→a.{(→b+→c)×→a+→b+→c}=0
2. for any three coplanar vectors →d,→e,→f,(→d×→e).→f=0
View Solution
