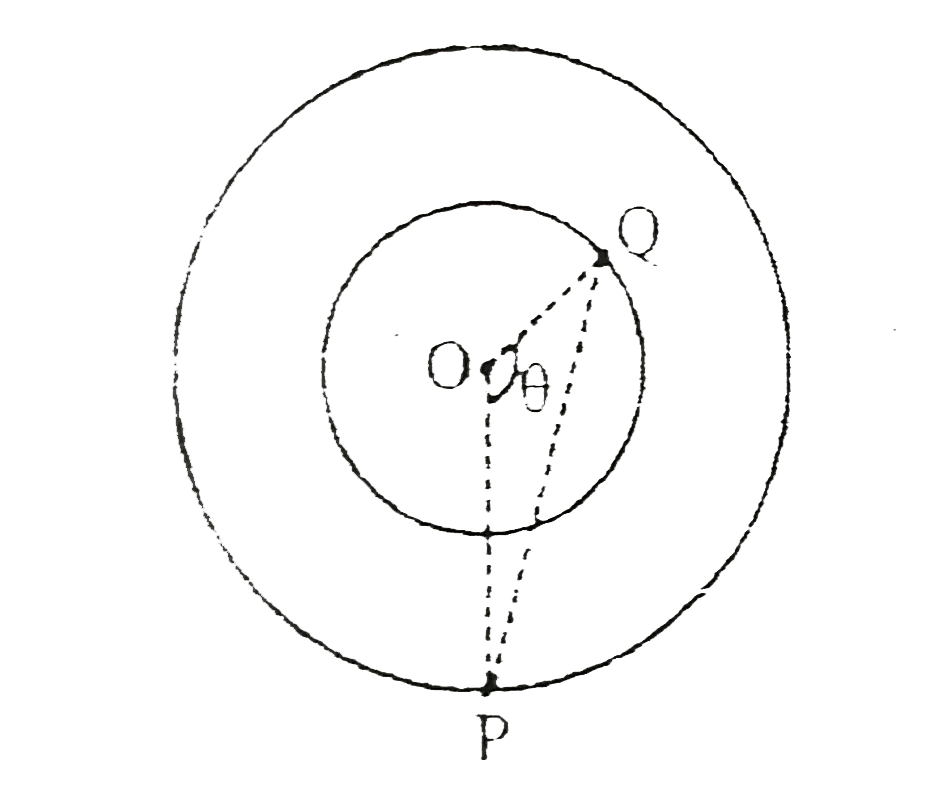
Two particles P and Q describe coplanar concentric circles of radii a and a' with angular velocities ω and ω', (in the same sense ) respectively. If the angular velocity of P with respect to Q is x, then fill 49x12 in OMR sheet. Take θ=2π3,a=2m,a'=1m,ω=2rad/s &ω'=1rad/s.
The correct Answer is:7
Let angle OPQ and PQO are a and b respectively when angle POQ =θ. As the particles P and Q move with constant angular speeds in their respectively circles, the velocity of point P and Q are
VP=aw and VQ=a'ω' respectively
Now the angluar velocity of P relative to Q is
ωr=aωcosd+a'ω'cosβd
=aω[a2+d2−a'22ad]+a'ω'[a'2+d2−a22a'd]d
=(ω+ω')2+(ω+ω')(a2−a'2)2(s2+a'2−2aa'cosθ)
If ωr=0 then cosθ=a2ω+a'2ω'2aa'(ω+ω)
Topper's Solved these Questions
- TEST PAPERSBOOK - BANSALCHAPTER - TEST PAPERSEXERCISE - PHYSICS PART A
35 Videos
- TEST PAPERSBOOK - BANSALCHAPTER - TEST PAPERSEXERCISE - PHYSICS PART B
3 Videos
- TEST PAPERSBOOK - BANSALCHAPTER - TEST PAPERSEXERCISE - PHYSICS PART (B)
3 Videos
- SEMICONDUCTORSBOOK - BANSALCHAPTER - SEMICONDUCTORSEXERCISE - CBSE Question
32 Videos
Similar Questions
Two discs A and B are in contact and rotating with angular velocity with angular velocities ω1andω2 respectively as shown. If there is no slipping between the discs, then

View SolutionTwo discs A and B are in contact and rotating with angular velocity with angular velocities ω1andω2 respectively as shown. If there is no slipping between the discs, then

View Solution
Knowledge Check
the angular velocity omega of a particle varies with time t as ω=5t2+25rads. the angular acceleration of the particle att=1s is
A10rads2B5rads2CZeroD3rads2A particle is moving with uniform speed 0.5m/s along a circle of radius 1m then the angular velocity of particle is (in rads−1)
A2B1.5C1D0.5A particle describes uniform circular motion in a circle of radius 2 m, with the angular speed of 2 rad s−1. The magnitude of the change in its velocity in π2 s is
A0ms−1B2√2ms−1C8ms−1D4ms−1
the angular velocity omega of a particle varies with time t as ω=5t2+25rads. the angular acceleration of the particle att=1s is
View SolutionTwo particles A and B are moving in a horizontal plane anitclockwise on two different concentric circles with different constant angular velocities 2ω and ω respectively. Find the relative velocity (in m/s) of B w.r.t. A after tome t=π/ω. They both start at the position as shown in figure (Takeω=3rad/sec,r=2m)
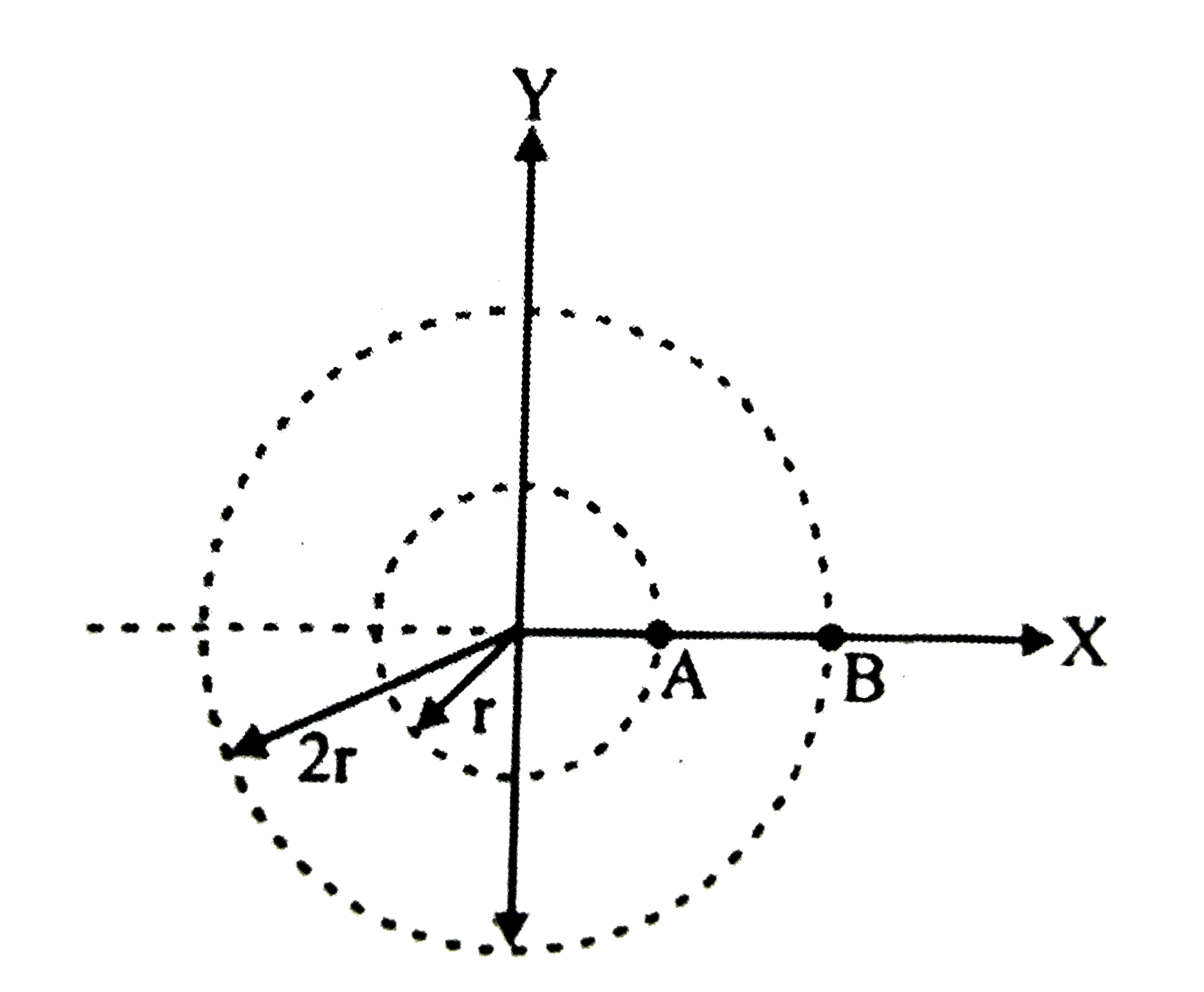
View SolutionTwo particles A and B are moving in a horizontal plane anitclockwise on two different concentric circles with different constant angular velocities 2ω and ω respectively. Find the relative velocity (in m/s) of B w.r.t. A after tome t=π/ω. They both start at the position as shown in figure (Takeω=3rad/sec,r=2m)

View SolutionTwo particle 'A' and 'B' are moving on the same circle with angular ω1 and ω2 respectively w.r.t. the centre of circle. Find the angular velocity of 'A' w.r.t. 'B' when,
(i) their sense of rotations is same,
(ii) and their sense of rotation is opposite.

View SolutionTwo particles A and B are moving in a horizontal plane anticlockwise on two different concentric circles with different constant angular velocities 2ω and ω,respectively. Find the relative velocity (in' ms ) of B w.r.t. A after time t=πω.(Takeomega=3 rad / s, r=2)
'(##CEN_KSR_PHY_JEE_C07_025_Q14##)'
View Solution
