A body is projected verticallt upwards. If t1 and t2 be the times at which it is at a height h above the point of projection while ascending and descending respectively, then:
h=gt1t2
h=2gt1t2
h=12gt1t2
h=14gt1t2
The correct Answer is:C
To solve the problem, we need to analyze the motion of a body projected vertically upwards. We will derive the relationship between the times t1 and t2 when the body is at a height h during its ascent and descent.
1. Understanding the Motion:
- When a body is projected upwards with an initial velocity u, it will ascend to a maximum height and then descend back down. The times t1 and t2 correspond to the moments when the body is at height h during its ascent and descent, respectively.
2. Using the Equation of Motion:
- The height h at any time t can be expressed using the equation of motion:
h=ut−12gt2
- Here, g is the acceleration due to gravity (acting downwards).
3. Setting Up the Equation:
- For the height h at time t1 (ascent):
h=ut1−12gt21
- For the height h at time t2 (descent):
h=ut2−12gt22
4. Rearranging the Equations:
- Rearranging both equations gives:
12gt21−ut1+h=0(1)
12gt22−ut2+h=0(2)
5. Identifying the Quadratic Equation:
- Both equations (1) and (2) are quadratic in form. The general form is at2+bt+c=0.
- For both equations, we can identify:
- a=12g
- b=−u
- c=h
6. Using the Product of Roots:
- For any quadratic equation at2+bt+c=0, the product of the roots t1 and t2 is given by:
t1t2=ca
- Substituting our values:
t1t2=h12g=2hg
7. Final Relationship:
- Rearranging gives us:
12gt1t2=h
- This is the required relationship between the times t1 and t2 when the body is at height h.
Conclusion:
The final result is:
12gt1t2=h
- When a body is projected upwards with an initial velocity u, it will ascend to a maximum height and then descend back down. The times t1 and t2 correspond to the moments when the body is at height h during its ascent and descent, respectively.
- The height h at any time t can be expressed using the equation of motion:
h=ut−12gt2
- Here, g is the acceleration due to gravity (acting downwards).
- For the height h at time t1 (ascent):
h=ut1−12gt21
- For the height h at time t2 (descent):
h=ut2−12gt22
- Rearranging both equations gives:
12gt21−ut1+h=0(1)
12gt22−ut2+h=0(2)
- Both equations (1) and (2) are quadratic in form. The general form is at2+bt+c=0.
- For both equations, we can identify:
- a=12g
- b=−u
- c=h
- For any quadratic equation at2+bt+c=0, the product of the roots t1 and t2 is given by:
t1t2=ca
- Substituting our values:
t1t2=h12g=2hg
- Rearranging gives us:
12gt1t2=h
- This is the required relationship between the times t1 and t2 when the body is at height h.
The final result is:
12gt1t2=h
Topper's Solved these Questions
- TEST PAPERSBOOK - BANSALCHAPTER - TEST PAPERSEXERCISE - PHYSICS PART (A)
32 Videos
- TEST PAPERSBOOK - BANSALCHAPTER - TEST PAPERSEXERCISE - PHYSICS PART (B)
3 Videos
- TEST PAPERSBOOK - BANSALCHAPTER - TEST PAPERSEXERCISE - PHYSICS PART- C
4 Videos
- SEMICONDUCTORSBOOK - BANSALCHAPTER - SEMICONDUCTORSEXERCISE - CBSE Question
32 Videos
Similar Questions
A body is vertically upwards. If t1 and t2 are the times at which it is height h above the point of projection while ascending and descending, respectively, find (a) the velocity of projection and height h, (b) the maximum height reached by the body and (c ) the velocity of the body at height h/2.
View SolutionA particle is projected vertically upwards from a point O on the ground. It takes time t1 to reach a point A at a height h above the ground, it continues to move and takes a time t2 to reach the ground. Find (a) h, (b) the maximum height reached and (c ) the velocity of the partical at the half of maximum height.
View Solution
Knowledge Check
A body is projected vertically upward from the surface of the earth, then the velocity-time graph is:-
A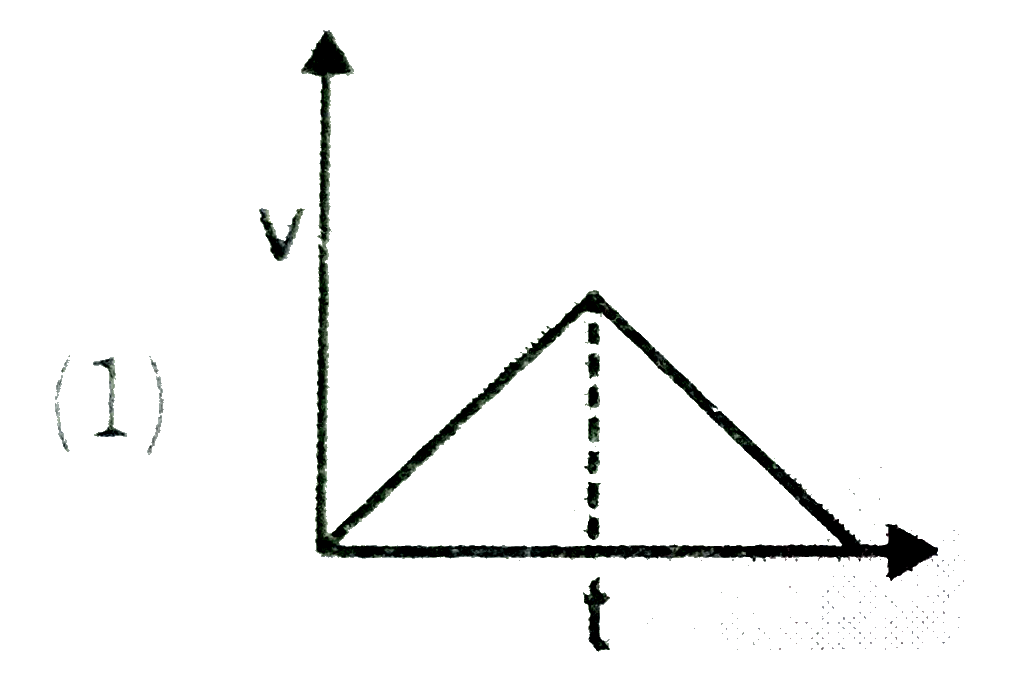 B
B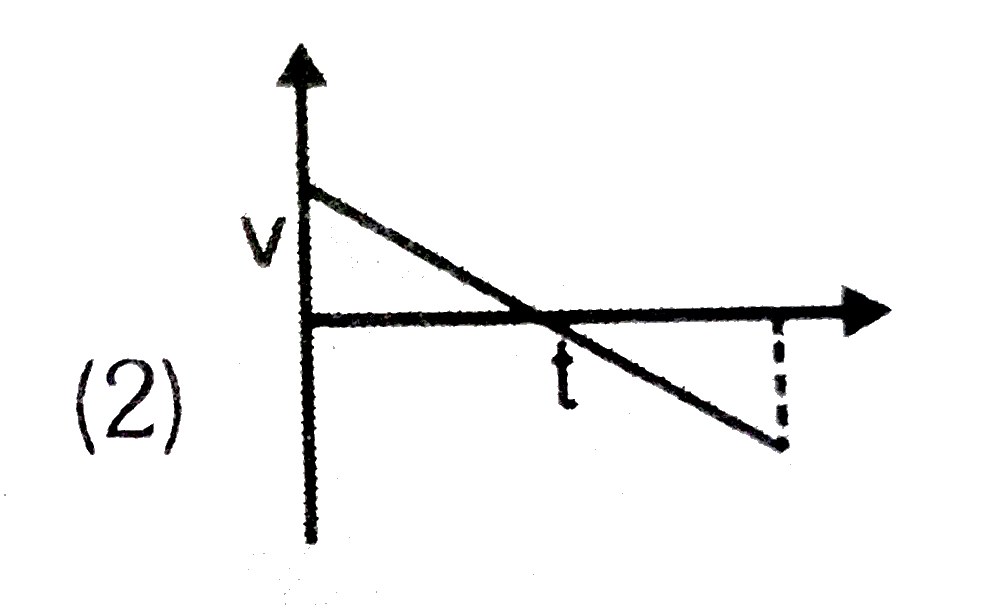 C
C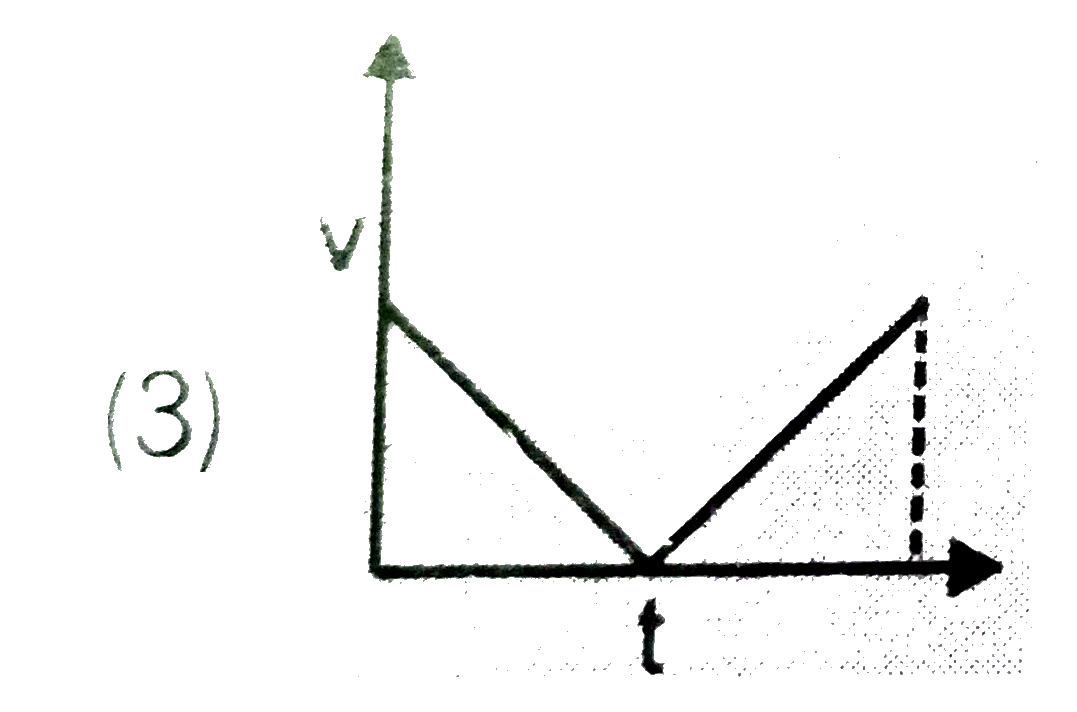 D
D
A body is projected veritclaly upwards.The times corresponding to height h while ascending and while descending are t1 and t2 respectively.
Then, the velocity of projection will be (take g as acceleration due to gravity)Ag√t1t22Bg(t1+t2)2Cg√t1t2Dgt1t2(t1+t2)A particle is projected vertically upwards and it reaches the maximum height H in time T seconds. The height of the particle at any time t will be-
Ag(t−T)2BH−12g(t−T)2Cg(t−T)2DH−g(t−T)
A particle is projected vertically upwards. Prove that it will be at three-fourth of its greatest height at times which are in the ratio 1:3.
View SolutionA body is projected vertically upwards at time "t=0" and it is seen at a height H at instants t_(1) and t_(2)seconds during its flight.The maximum height attained is (g is acceleration due to gravity
View SolutionA stone is projected vertically upwards. Its height h at time t sec is h=(80)t−(16)t2. The velocity with which it hits the ground is
View SolutionA particle is projected vertically upwards and reaches the maximum height H in time T. The height of the partlcle at any time t(<T) will be
View SolutionA body is projected up with a speed u and the time taken by it is T to reach the maximum height H. Pich out the correct statement
View Solution
