A rotor is rotating with a constant angular velocity ω about its own axis. At the centre of the rotor a spring is fixed of nature length (l0) whose other end is connected to a block of mass m. Find the minimum value of coefficient of friction between block and rotor wall for which spring remains horizontal. The radius of rotor is R(R>l0).

mgmω2R+K(R−l0)
mgmω2R−K(R−l0)
mg(mω2+K)R
mg(mω2−K)R
The correct Answer is:B
N=mω2R−K(R−l0) ….(1)

For the block to remains in the vertical equilibrium,
f = mg
⇒N=mg
⇒μ(mω2R−K(R−l0)=mg
[from equation (1)]
∴μ=mgmω2R−K(R−l0)
Topper's Solved these Questions
- TEST PAPERSBOOK - BANSALCHAPTER - TEST PAPERSEXERCISE - PHYSICS PART (A)
32 Videos
- TEST PAPERSBOOK - BANSALCHAPTER - TEST PAPERSEXERCISE - PHYSICS PART (B)
3 Videos
- TEST PAPERSBOOK - BANSALCHAPTER - TEST PAPERSEXERCISE - PHYSICS PART- C
4 Videos
- SEMICONDUCTORSBOOK - BANSALCHAPTER - SEMICONDUCTORSEXERCISE - CBSE Question
32 Videos
Similar Questions
One end of a light spring constant k and natural length l0 is fixed and the other end is attached to a block of mass m lying on smooth horizontal surface. If the block is rotating in the horizontal circle of radius l, find the frequency of the revolution.
View SolutionTwo small blocks of mass mA=30 kg & mB =15 kg are connected with spring & kept on the wedge which is rotating about given axis as shown in figure. If blocks B remain in rest then minimum value of coefficient of friction between block A & wedge is μ0, then the value of μ20 is :
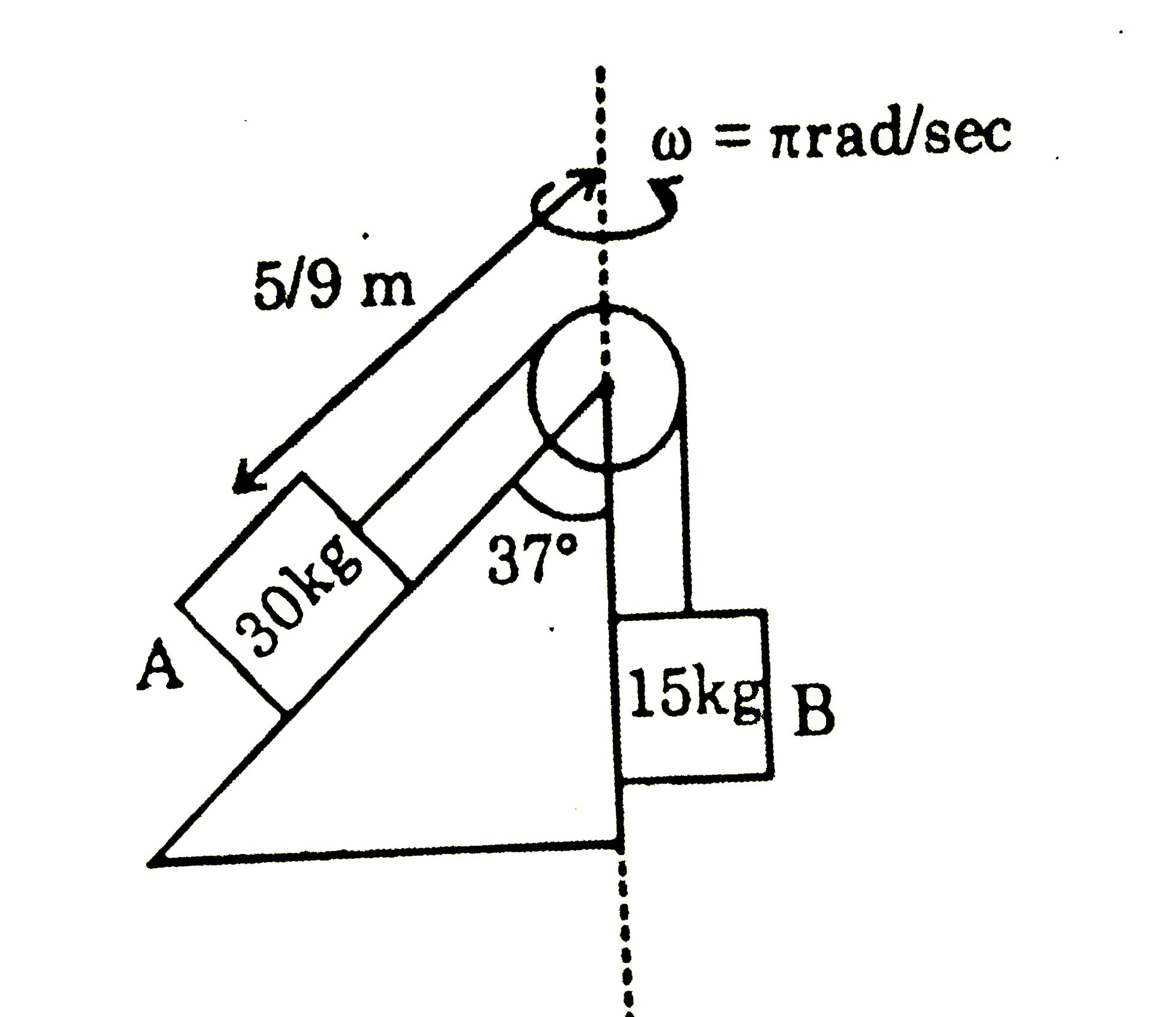
View Solution
Knowledge Check
A rotor is rotating with a constant angular velocity ω about its own axis. At the centre of the rotaor a spring is fixed of natural length (l0) whose other end is connected to a block of mass m. Find the minimum vaule of coefficient of friction between block and rotor wall for which spring remains horizontal. The radius of rotor is R(R<l0).
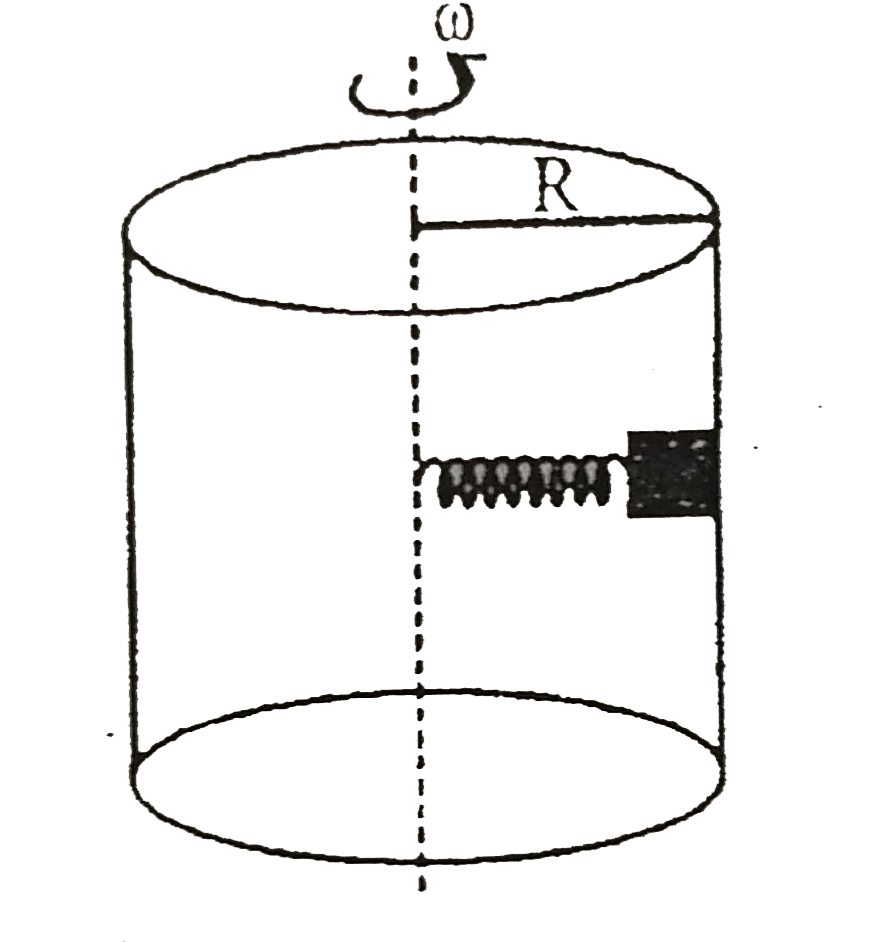 Aμ=mgmω2R+K(l0−R)Bμ=mgK(l0−R)Cμ=mgmω2R−K(l0−R)Dμ=mgKR
Aμ=mgmω2R+K(l0−R)Bμ=mgK(l0−R)Cμ=mgmω2R−K(l0−R)Dμ=mgKRA block of mass m is pressed against a wall by a spring as shown in the figure. The spring has natural length , l(l>L), and the coefficient of friction between the block and the wall is μ . The minimum spring constant K necessary for equilibrium is:
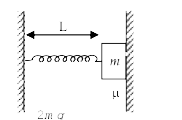 A2mgμ(l−L)Bmgμ(l−L)Cmg2μ(l−L)D2mgμl
A2mgμ(l−L)Bmgμ(l−L)Cmg2μ(l−L)D2mgμlA hollow vertical cylinder of radius R is rotated with angular velocity ω about an axis through its centre. What is the minimum coefficient of static friction between block M and cylinder wall necessary to keep the block suspended on the inside of the cylinder ?
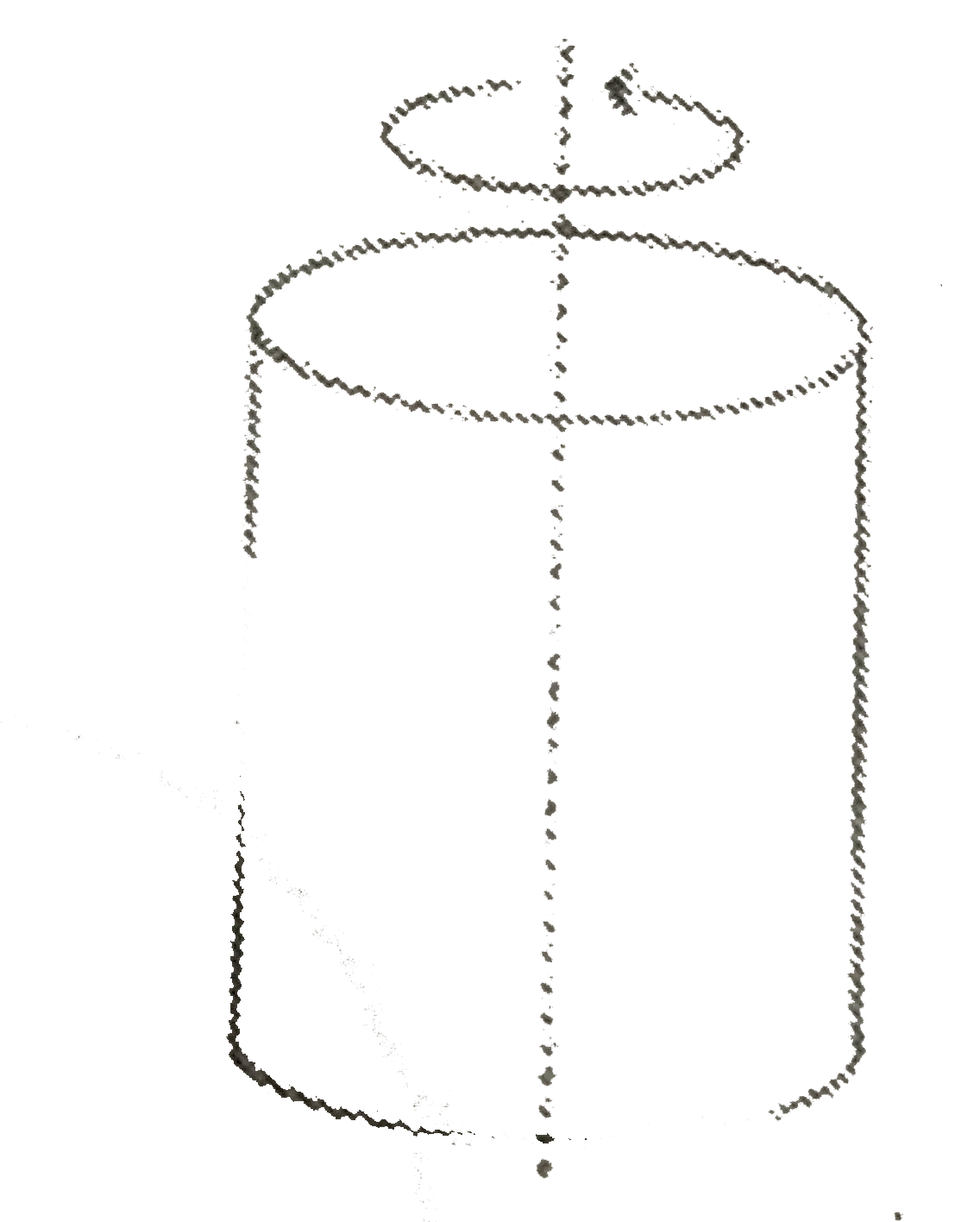 Aμ=gRω2Bμ=ω2gRCμ=ω2RgDμ=gω2R
Aμ=gRω2Bμ=ω2gRCμ=ω2RgDμ=gω2R
A block of mass m is pressed against a wall by a spring as shown in the figure. The spring has natural length , l(l>L), and the coefficient of friction between the block and the wall is μ . The minimum spring constant K necessary for equilibrium is:

View SolutionA hollow vertical cylinder of radius R is rotated with angular velocity ω about an axis through its centre. What is the minimum coefficient of static friction between block M and cylinder wall necessary to keep the block suspended on the inside of the cylinder ?

View SolutionIn the figure shown, a spring of spring constant K is fixed at on end and the other end is attached to the mass 'm' . The coefficient of friction between block and the inclined plane is μ. The block is released when the spring is in tis natural length. Assuming that the θ>μ, the maximum speed of the block during the motion is.
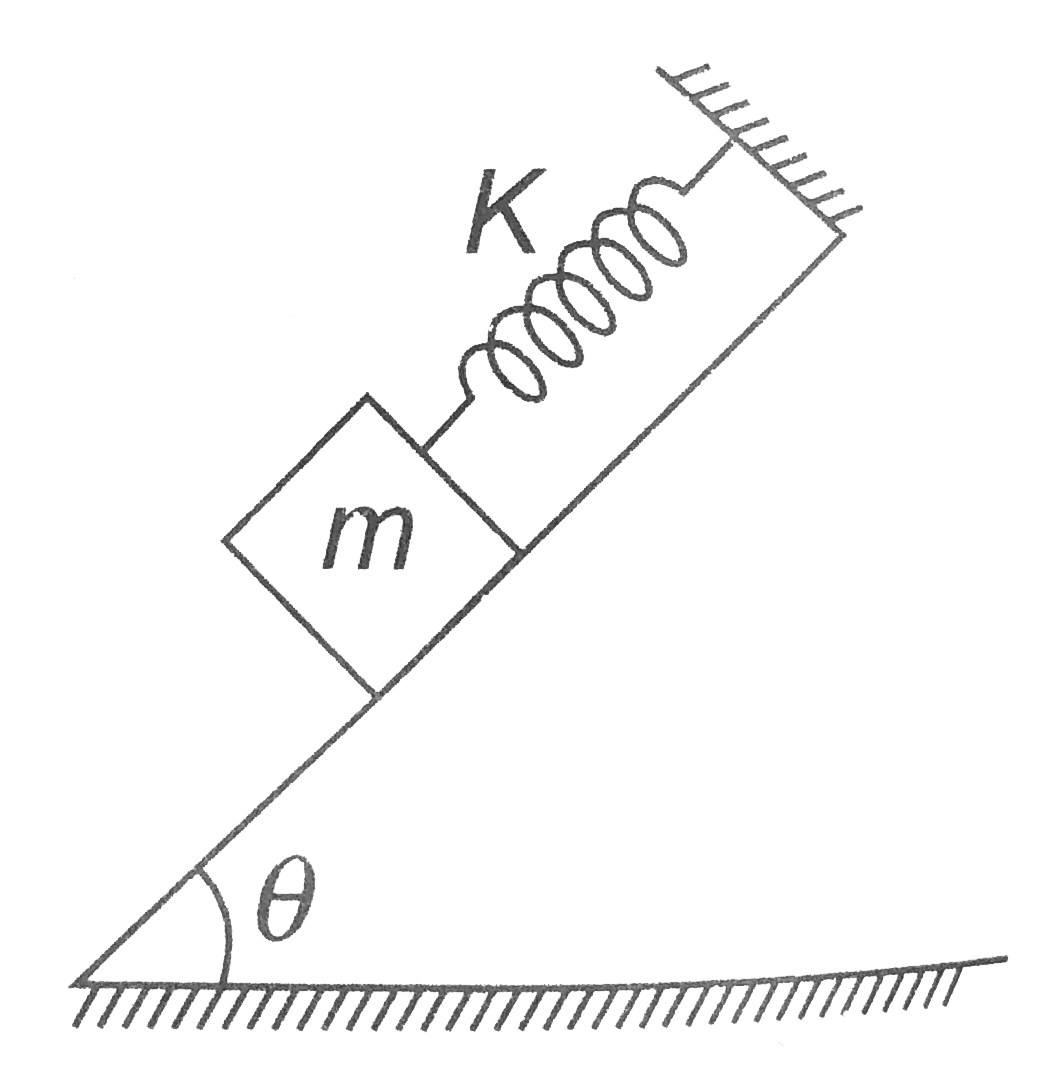
View SolutionA disc of radius 4m is rotating about its fixed centre with a constant angular velocity 2rads (in the horizontal plane).A block is also rotating with the disc without slipping. If co-efficient of friction between the block and the disc is 0.4 ,then the maximum distance at which the block can rotate without
View SolutionIn the figure shown, a spring of spring constant K is fixed at on end and the other end is attached to the mass 'm' . The coefficient of friction between block and the inclined plane is μ. The block is released when the spring is in tis natural length. Assuming that the θ>μ, the maximum speed of the block during the motion is.

View Solution
