A stone is projected at an angle to the horizontal from the top of a tower of height 3h If the stone reaches a maximum height h above the tower, then calculate the distance from the foot of the tower where particle strikes the foot of the where particle strikes the ground.
The correct Answer is:B
Range
Topper's Solved these Questions
- TEST PAPERSBOOK - BANSALCHAPTER - TEST PAPERSEXERCISE - PHYSICS PART (A)
32 Videos
- TEST PAPERSBOOK - BANSALCHAPTER - TEST PAPERSEXERCISE - PHYSICS PART (B)
3 Videos
- TEST PAPERSBOOK - BANSALCHAPTER - TEST PAPERSEXERCISE - PHYSICS PART- C
4 Videos
- SEMICONDUCTORSBOOK - BANSALCHAPTER - SEMICONDUCTORSEXERCISE - CBSE Question
32 Videos
Similar Questions
A stone is projected at an angle α to the horizontal from the top of a tower of height 3h. If the stone reaches a maximum height 'h', above the tower, show that it reaches the ground at a distance 6h cot α from the foot of the lower.
View SolutionA stone is dropped from the top of a tower of height 100 m. The stone penetrates in the sand on the ground through a distance of 2m. Calculate the retardation of the stone.
View Solution
Knowledge Check
a body is thrown horizontally with a velocity √2gh from the top of a tower of height h. It strikes the level gound through the foot of the tower at a distance x from the tower. The value of x is :-
AhBh/2C2hD2h/3A stone dropped from the top of a tower reaches the ground in 3 s. The height of the tower is
A18.6 mB39.2 mC44.1 mD98 mAt a distance 2h m from the foot of a tower of height h m,the top of the tower and a pole at the top of the tower subtend equal angles height of the pole should be
A(5h)/3mB(4h)/3mC(7h)/5mD(3h)/2m
A particle is projected from a tower as shown in figure, then find the distance from the foot of the tower where it will strike the ground. (g=10m/s2)
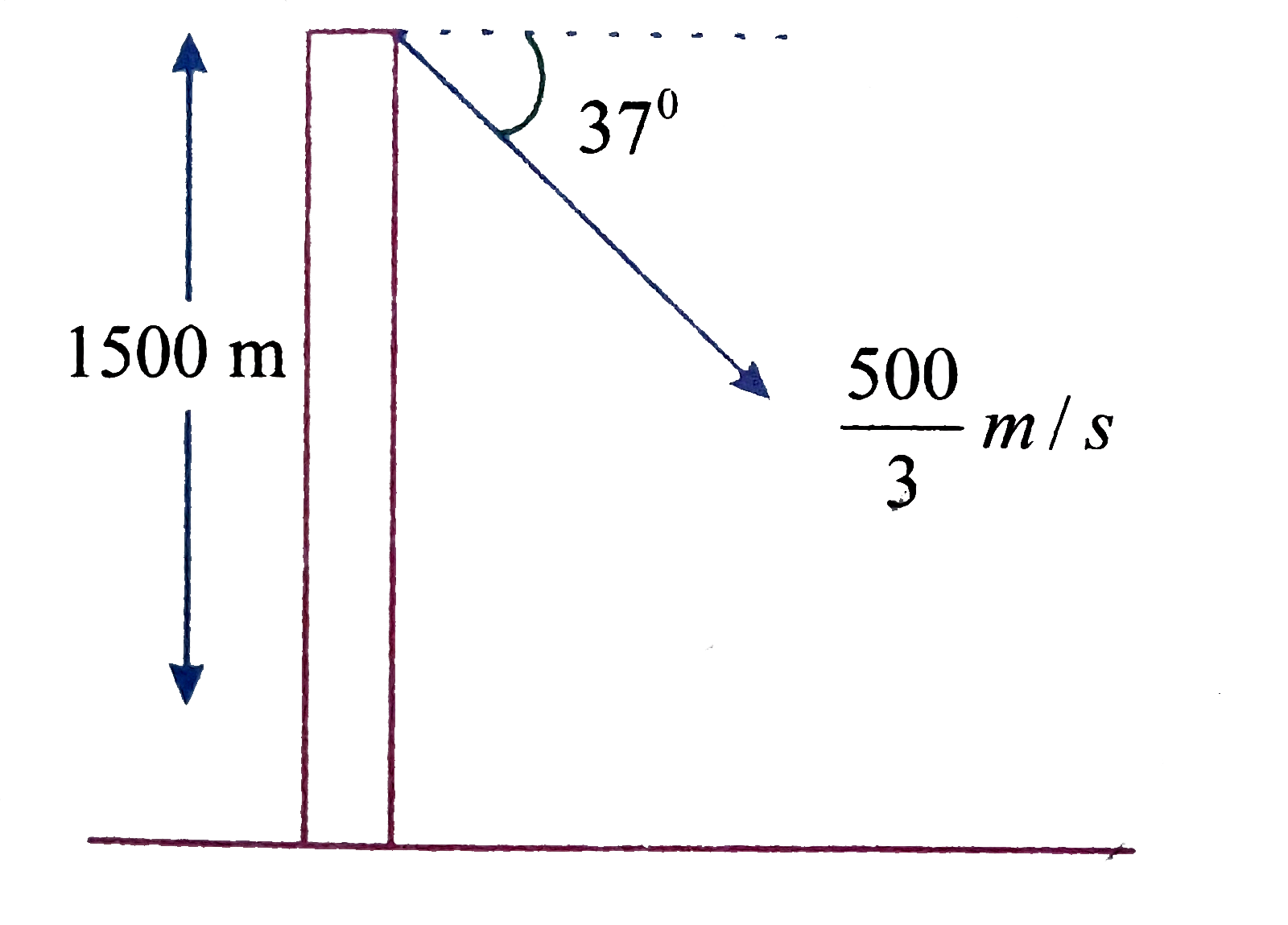
View SolutionA ball is thrown with velocity 40m/s at angle 30∘ with horizontal from the top of a tower of height 60m. At what horizontal distance from the foot of tower, the ball will strike the gorund ?
View SolutionFrom the foot of a tower 80m high, a stone is thrown up so as to reach the top of a tower. After 2s, another stone is dropped from the top of the tower. When and where the two stones meet?
View SolutionAt a distance 2h m from the foot of a tower of height h m,the top of the tower and a pole at the top of the tower subtend equal angles height of the pole should be
View SolutionA body of mass m is projected horizontally with a velocity v from the top of a tower of height h and it reaches the ground at a distance x from the foot of the tower. If a second body of mass 2m is projected horizontally from the top of a tower of height 2h, it reaches the ground at a distance 2x from the foot of the tower. The horizontal velocity of the second body is :
View Solution
