From a solid cylined of length 4R and radius R, two hemispheres of radius R and R2 are cut from both the ends as shown. The location of new centre of mass from point O is approximately
From a solid cylined of length 4R and radius R, two hemispheres of radius R and (R )/(2) are cut from both the ends as shown. The location of new centre of mass from point O is approximately

A

3R

B

2R

C

3R2

D

R

Text Solution
Verified by Experts

The correct Answer is:D

N1x1−N2x2−N3x3N1−N2−N3

Doubtnut Promotions Banner
|
Class 12PHYSICSQUESTION BANK

Topper's Solved these Questions

Similar Questions

Knowledge Check

  • A uniform solid right circular cone of base radius R is joined to a uniform solid hemisphere of radius R and of the same density, as shown. The centre of mass of the composite solid lies at the centre of base of the cone. The height of the cone is
    ocr_image

    A1.5R
    B√3R
    C3R
    D2√3R

  • From a uniform disc of radius R, an equilibatered triangle of side √3R is cut as shown. The new position of centre of mass is:
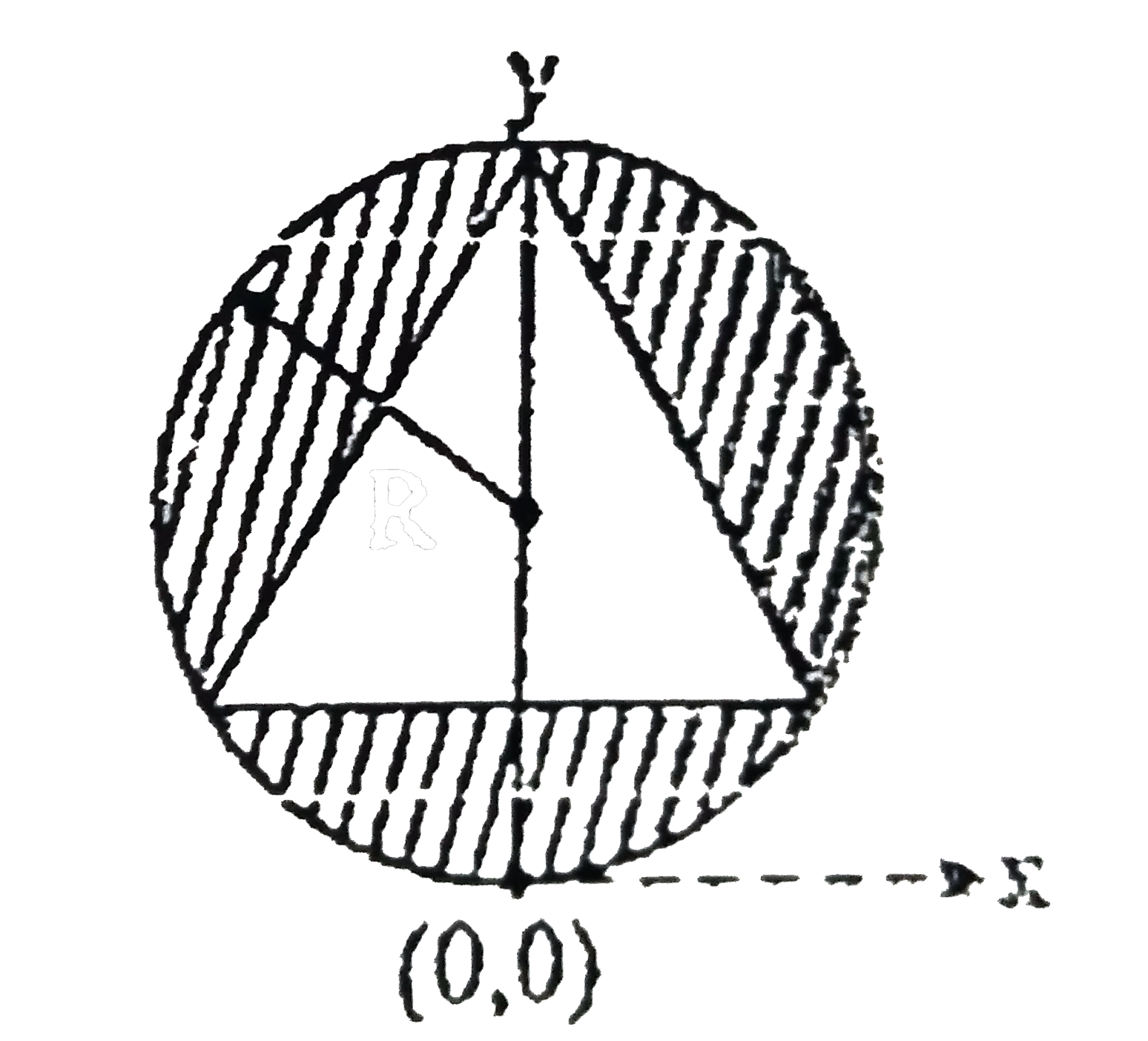    ocr_image

    A(0,0)
    B(0,R)
    C(0,√3R2)
    Dnone of these

  • A solid sphere of mass m & radius R is cut into two equal parts and kept as shown. Find the height of centre of mass from the ground.
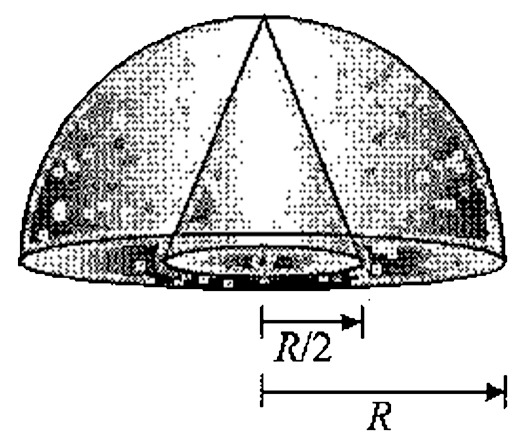
    ocr_image

    AR2
    B3R8
    C7R8
    D9R8