The French physicist Louis de Brogie in 1924 postulated that matter, like radiation, should exhibit a dual behaviour. He proposed the following relationship between the wavelength of a material particle, its linear momentum p and planck constant h.
The de Broglie relation implies that the wavelength of a particle should decrease as its velocity increase. its also implies that for a given velocity heavier particles should have shorter wavelength than lighter particles. The waves associated with particles in motion are called matter waves or de Broglie waves. These waves differe from the electromagnetic waves as they
(i) have lower velocites
(ii) have no electrcal and magnetic fields, and
(iii) are not emitted by the particle under consideration. The experimental confirmation of the de Brgolie's relation was obtained when Davisson and Germer, in 1927, observed that a beam of electron is diffracted by a nickel crystal. As diffraction is a characterstic property of waves hence the beam of electron behaves as a wave, as proposed by de Broglie
An electron is accelerated from rest and it has wavelength of be how much amount potential should be dropped so that wavelength associated with electron becomes
The correct Answer is:A
Topper's Solved these Questions
Similar Questions
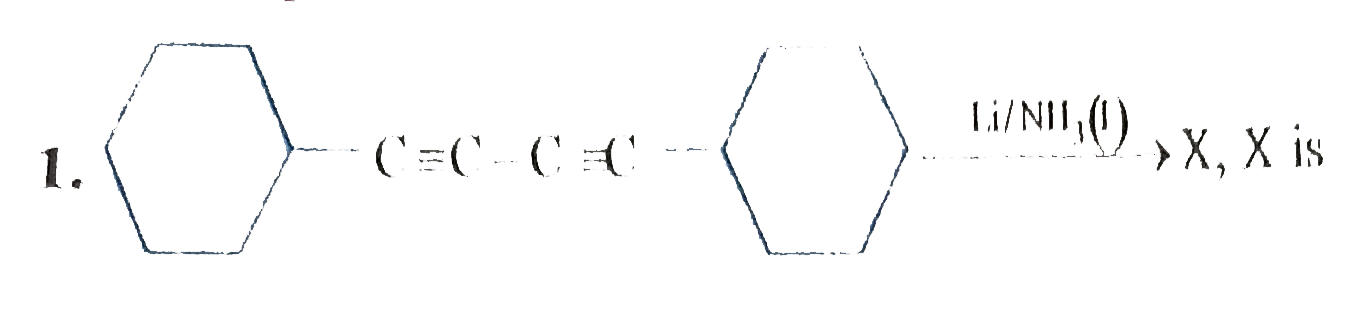
Complete the following reaction
 02:27View Solution
02:27View Solution
Identify the position where electrophilic aromatic substitution EAS) is most favourable05:44View SolutionThe French physicist Louis de Broglie in 1924 postulated that matter like radiation , should exhibit a dual behaviour. He proposed the following relationship between the wavelength .λ of a material particle,its linear momentum P and Planck constant h.
λ=hp=hmv
The de Broglie relaion that the wavelength of a particle should decrease as its velocity increases. It also implies that for a given velocity heavier particles should have shorter wavelength than lighter particles.The waves or de Broglie waves. These waves differ from the electromagnetic waves as they:
(i) have lower velocities
(ii) have no electrical and magnetic fields and
(iii) are not emitted by the particle under consideration.
The expermental confirmation of the de Broglie relation was obtained when Davission and Germer in 1927, observed. As diffraction is a characteristic property of waves, hence the beam of electrons behave as a wave as proposed by de Broglie.
Werner Heisenberg considered the limits of how precisely we can measure properties of an electron or other microscopic particle like electron . He determined that there is a fundamental limit of how closely we can measure both position and momentum. The more accurately we can determine its position. The converse is also true. This is summed up in what we now call the ''Heisenberg uncertainty principle'' : It is impossible to determine simultaneously and precisely both the momentum and position of a particle. The product of uncertainty in the position, Δx and the uncertainty in the momentum Δ(mv) must be greater than or equal to h4π,i.e.,
ΔxΔ(mv)≥h4π
The correct order of wavelength of Hydrogen (.1H1) Deuterium (.1H2) and Tritium (.1H3) moving with same kinetic energy is :02:58View SolutionThe French physicist Louis de Broglie in 1924 postulated that matter like radiation , should exhibit a dual behaviour. He proposed the following relationship between the wavelength .λ of a material particle,its linear momentum P and Planck constant h.
λ=hp=hmv
The de Broglie relaion that the wavelength of a particle should decrease as its velocity increases. It also implies that for a given velocity heavier particles should have shorter wavelength than lighter particles.The waves or de Broglie waves. These waves differ from the electromagnetic waves as they:
(i) have lower velocities
(ii) have no electrical and magnetic fields and
(iii) are not emitted by the particle under consideration.
The expermental confirmation of the de Broglie relation was obtained when Davission and Germer in 1927, observed. As diffraction is a characteristic property of waves, hence the beam of electrons behave as a wave as proposed by de Broglie.
Werner Heisenberg considered the limits of how precisely we can measure properties of an electron or other microscopic particle like electron . He determined that there is a fundamental limit of how closely we can measure both position and momentum. The more accurately we can determine its position. The converse is also true. This is summed up in what we now call the ''Heisenberg uncertainty principle'' : It is impossible to determine simultaneously and precisely both the momentum and position of a particle. The product of uncertainty in the position, Δx and the uncertainty in the momentum Δ(mv) must be greater than or equal to h4π,i.e.,
ΔxΔ(mv)≥h4π
The transition so that the de Broglie wavelength of electron becomes 3 times of its initial value in He+ ion will be :02:27View SolutionThe French physicist Louis de Broglie in 1924 postulated that matter like radiation , should exhibit a dual behaviour. He proposed the following relationship between the wavelength .lambda of a material particle,its linear momentum P and Planck constant h. lambda=(h)/(p)=(h)/(mv) The de Broglie relaion that the wavelength of a particle should decrease as its velocity increases. It also implies that for a given velocity heavier particles should have shorter wavelength than lighter particles.The waves or de Broglie waves. These waves differ from the electromagnetic waves as they: (i) have lower velocities (ii) have no electrical and magnetic fields and (iii) are not emitted by the particle under consideration. The expermental confirmation of the de Broglie relation was obtained when Davission and Germer in 1927, observed. As diffraction is a characteristic property of waves, hence the beam of electrons behave as a wave as proposed by de Broglie. Werner Heisenberg considered the limits of how precisely we can measure properties of an electron or other microscopic particle like electron . He determined that there is a fundamental limit of how closely we can measure both position and momentum. The more accurately we can determine its position. The converse is also true. This is summed up in what we now call the ''Heisenberg uncertainty principle'' : It is impossible to determine simultaneously and precisely both the momentum and position of a particle. The product of uncertainty in the position, Deltax and the uncertainty in the momentum Delta(mv) must be greater than or equal to (h)/(4pi), i.e., Deltax Delta(mv)ge(h)/(4pi) If the uncertainty in velocity and posititon is same then the uncertainty in momentum will be :
05:44View SolutionThe French physicist Louis de Broglie in 1924 postulated that matter , like radiation , should exhibit dual behaviour. He proposed the following relationship between the wavelenght lambda of a material particle , its linear momentum p and planck cosntant h.
λ=hp=hmv
The de Broglie relation implies that the wavelength of a partices should decreases as its velocity increases. It also implies that the for a given velocity heavir particule should have shorter wavelenght than lighter particles. The waves associated with particles in motin are called matter waves or de Broglie waves.
These waves differ from the electromagnetic waves as they
(i) have lower velocities
have no electrical and magnetic fields and
are not emitted by the particle under consideration.
The experimental confirmation of the de Broglie relation was obtained when Davisson and Germer. in
1927, observed that a beam of electrons is diffracted by a nickel arystal. As diffarceted by a nickel . As diffraction is a characteristic
property of waves, hence the beam of electron dehaves as a wave, as proposed by de Broglie.
Werner Heisenberg cobnsiderd the imits of how precisely we can measure propoerties of an electron or
other microscopic particle like electron. he determined that there is accurately we measure the momentum of a
particle, the less accurately we can determine its position . The converse is laso true . The is summed up
in what we now call the "Hesienberg uncertainty princple: It isimpossibble to determine simultameously ltbr> and percisely both the momentum ans position of particle . The product of uncertainly in the position,
Deltax and the ncertainly in the momentum Delta(mv) mudt be greater than or equal to h4π i.e.
ηΔxΔ(mv)≥h4π
The correct order of wavelenght of Hydrogen (.1H1) Deuterium (.1H2) and Tritium (.1H3) moving withsame kinetic energy is.02:43View SolutionThe French physicist Louis de Broglie in 1924 postulated that matter , like radiation , should exhibit dual behaviour. He proposed the following relationship between the wavelenght lambda of a material particle , its linear momentum p and planck cosntant h. lambda= (h)/(p)=(h)/(mv) The de Broglie relation implies that the wavelength of a partices should decreases as its velocity increases. It also implies that the for a given velocity heavir particule should have shorter wavelenght than lighter particles. The waves associated with particles in motin are called matter waves or de Broglie waves. These waves differ from the electromagnetic waves as they (i) have lower velocities have no electrical and magnetic fields and are not emitted by the particle under consideration. The experimental confirmation of the de Broglie relation was obtained when Davisson and Germer. in 1927, observed that a beam of electrons is diffracted by a nickel arystal. As diffarceted by a nickel . As diffraction is a characteristic property of waves, hence the beam of electron dehaves as a wave, as proposed by de Broglie. Werner Heisenberg cobnsiderd the imits of how precisely we can measure propoerties of an electron or other microscopic particle like electron. he determined that there is accurately we measure the momentum of a particle, the less accurately we can determine its position . The converse is laso true . The is summed up in what we now call the "Hesienberg uncertainty princple: It isimpossibble to determine simultameously ltbr> and percisely both the momentum ans position of particle . The product of uncertainly in the position, Deltax and the ncertainly in the momentum Delta(mv) mudt be greater than or equal to (h)/(4pi) i.e. etaDeltax Delta(mv)ge(h)/(4pi) Trhe transition , so that the de-Broglie wavelenght of electron becomes 3 times of its initial value in He^(+) ion will be.
01:05View SolutionThe French physicist Louis de Broglie in 1924 postulated that matter , like radiation , should exhibit dual behaviour. He proposed the following relationship between the wavelenght lambda of a material particle , its linear momentum p and planck cosntant h.
λ=hp=hmv
The de Broglie relation implies that the wavelength of a partices should decreases as its velocity increases. It also implies that the for a given velocity heavir particule should have shorter wavelenght than lighter particles. The waves associated with particles in motin are called matter waves or de Broglie waves.
These waves differ from the electromagnetic waves as they
(i) have lower velocities
have no electrical and magnetic fields and
are not emitted by the particle under consideration.
The experimental confirmation of the de Broglie relation was obtained when Davisson and Germer. in
1927, observed that a beam of electrons is diffracted by a nickel arystal. As diffarceted by a nickel . As diffraction is a characteristic
property of waves, hence the beam of electron dehaves as a wave, as proposed by de Broglie.
Werner Heisenberg cobnsiderd the imits of how precisely we can measure propoerties of an electron or
other microscopic particle like electron. he determined that there is accurately we measure the momentum of a
particle, the less accurately we can determine its position . The converse is laso true . The is summed up
in what we now call the "Hesienberg uncertainty princple: It isimpossibble to determine simultameously ltbr> and percisely both the momentum ans position of particle . The product of uncertainly in the position,
Deltax and the ncertainly in the momentum Delta(mv) mudt be greater than or equal to h4π i.e.
ηΔxΔ(mv)≥h4π
If the uncertainty in velocity & postional is same, then the uncertainity in momentum will be05:44View SolutionThe French physicist Louis de Brogie in 1924 postulated that matter, like radiation, should exhibit a dual behaviour. He proposed the following relationship between the wavelength λ of a material particle, its linear momentum p and planck constant h.
λ=hp=hmv
The de Broglie relation implies that the wavelength of a particle should decrease as its velocity increase. its also implies that for a given velocity heavier particles should have shorter wavelength than lighter particles. The waves associated with particles in motion are called matter waves or de Broglie waves. These waves differe from the electromagnetic waves as they
(i) have lower velocites
(ii) have no electrcal and magnetic fields, and
(iii) are not emitted by the particle under consideration. The experimental confirmation of the de Brgolie's relation was obtained when Davisson and Germer, in 1927, observed that a beam of electron is diffracted by a nickel crystal. As diffraction is a characterstic property of waves hence the beam of electron behaves as a wave, as proposed by de Broglie
If proton, electron and α-particle are moving with same kinetic energy then the order of their de-Broglie's wavelength.View SolutionThe French physicist Louis de Broglie in 1924 postulated that matter like radiation , should exhibit a dual behaviour. He proposed the following relationship between the wavelength .λ of a material particle,its linear momentum P and Planck constant h.
λ=hp=hmv
The de Broglie relaion that the wavelength of a particle should decrease as its velocity increases. It also implies that for a given velocity heavier particles should have shorter wavelength than lighter particles.The waves or de Broglie waves. These waves differ from the electromagnetic waves as they:
(i) have lower velocities
(ii) have no electrical and magnetic fields and
(iii) are not emitted by the particle under consideration.
The expermental confirmation of the de Broglie relation was obtained when Davission and Germer in 1927, observed. As diffraction is a characteristic property of waves, hence the beam of electrons behave as a wave as proposed by de Broglie.
Werner Heisenberg considered the limits of how precisely we can measure properties of an electron or other microscopic particle like electron . He determined that there is a fundamental limit of how closely we can measure both position and momentum. The more accurately we can determine its position. The converse is also true. This is summed up in what we now call the ''Heisenberg uncertainty principle'' : It is impossible to determine simultaneously and precisely both the momentum and position of a particle. The product of uncertainty in the position, Δx and the uncertainty in the momentum Δ(mv) must be greater than or equal to h4π,i.e.,
ΔxΔ(mv)≥h4π
The transition so that the de Broglie wavelength of electron becomes 3 times of its initial value in He+ ion will be :View SolutionThe French physical Louis de Broglie in 1924 postulated that matter, like radiation, should exhibit a dual behaviour. He proposed the following relationship between the wavelength lambda of a material particle, its linear momentum p and planck constant h. lambda=h/p=h/(mv) The de Broglie relation implies that the wavelength of a particle should decrease as its velocity increases. It also implies that for a given velocity heavier particles should have shorter wavelength than fighter particles.The wave associated with particles in motion are called matter waves or de Broglie waves.These waves differ from the electromagnetic waves as they (I)have lower velocities (II)have no electrical and magnetic fields and (III)are not emitted by the particle under consideration The experiment confirmation of the de Broglies relation was obtained when Davisson and Germer, in 1927, observed that a beam of electrons is diffrated by a nickel crystal.As diffraction is a characteristic property of waves hence the beam of electron behaves as a wave, as proposed by de broglie. Using Bohr's theory, the transition, so that the electrons de-Broglie wavelength becomes 3 times of its orginial value in He^+ ion will be
01:32View SolutionThe French physical Louis de Broglie in 1924 postulated that matter, like radiation, should exhibit a dual behaviour. He proposed the following relationship between the wavelength λ of a material particle, its linear momentum p and planck constant h.
λ=hp=hmv
The de Broglie relation implies that the wavelength of a particle should decrease as its velocity increases. It also implies that for a given velocity heavier particles should have shorter wavelength than fighter particles.The wave associated with particles in motion are called matter waves or de Broglie waves.These waves differ from the electromagnetic waves as they
(I)have lower velocities
(II)have no electrical and magnetic fields and
(III)are not emitted by the particle under consideration
The experiment confirmation of the de Broglies relation was obtained when Davisson and Germer, in 1927, observed that a beam of electrons is diffrated by a nickel crystal.As diffraction is a characteristic property of waves hence the beam of electron behaves as a wave, as proposed by de broglie.
De-Broglie wavelength of an electron travelling with speed equal to 1% of the speed of lightView SolutionThe de Broglie wavelength (lambda) of a particle is related to its kinetic energy E as
03:07View SolutionThe graph showing the correct variation of linear momentum (p) of a charge particle with its de-Broglie wavelength (λ) is
02:38View SolutionDual nature of matter was proposed by Louis de Broglie. a) Calculate the de Broglie wavelength associated with an electron with velocity equal to that of light .
05:03View Solution

