The number of nonzero integral values of a for which the function f(x)=x4+ax3+3x22+1 is concave upward along the entire real line is___________
To find the number of nonzero integral values of a for which the function
f(x)=x4+ax3+3x22+1
is concave upward along the entire real line, we need to analyze the second derivative of the function.
Step 1: Find the first derivative f′(x)
The first derivative f′(x) is calculated as follows:
f′(x)=ddx(x4)+ddx(ax3)+ddx(3x22)+ddx(1)
Calculating each term:
- ddx(x4)=4x3
- ddx(ax3)=3ax2
- ddx(3x22)=3x
- ddx(1)=0
Thus,
f′(x)=4x3+3ax2+3x
Step 2: Find the second derivative f′′(x)
Now, we differentiate f′(x) to find f′′(x):
f′′(x)=ddx(4x3)+ddx(3ax2)+ddx(3x)
Calculating each term:
- ddx(4x3)=12x2
- ddx(3ax2)=6ax
- ddx(3x)=3
Thus,
f′′(x)=12x2+6ax+3
Step 3: Determine conditions for concavity
For the function f(x) to be concave upward along the entire real line, the second derivative f′′(x) must be greater than or equal to zero for all x:
12x2+6ax+3≥0
Step 4: Analyze the quadratic inequality
The expression 12x2+6ax+3 is a quadratic in x. A quadratic Ax2+Bx+C is non-negative for all x if:
1. A>0 (which is true here since A=12>0)
2. The discriminant D must be less than or equal to zero:
D=B2−4AC
Substituting A=12, B=6a, and C=3:
D=(6a)2−4⋅12⋅3
Calculating D:
D=36a2−144
Setting the discriminant less than or equal to zero:
36a2−144≤0
Step 5: Solve the inequality
Dividing the entire inequality by 36:
a2−4≤0
This factors to:
(a−2)(a+2)≤0
The solution to this inequality is:
−2≤a≤2
Step 6: Identify nonzero integral values
The integral values of a in the interval (−2,2) are:
- −2
- −1
- 1
- 2
Thus, the nonzero integral values are:
- −1
- 1
- 2
Conclusion
The number of nonzero integral values of a is:
Answer: 3
- ddx(ax3)=3ax2
- ddx(3x22)=3x
- ddx(1)=0
- ddx(3ax2)=6ax
- ddx(3x)=3
2. The discriminant D must be less than or equal to zero:
- −1
- 1
- 2
- 1
- 2
Similar Questions
Concavity and convexity :
if f''(x)>0∀x∈(a,b) then the curve y=f(x) is concave up ( or convex down) in (a,b) and iff''(x)<0∀x∈(a,b) then the curve y=f(x) is concave down (or convex up ) in (a,b)
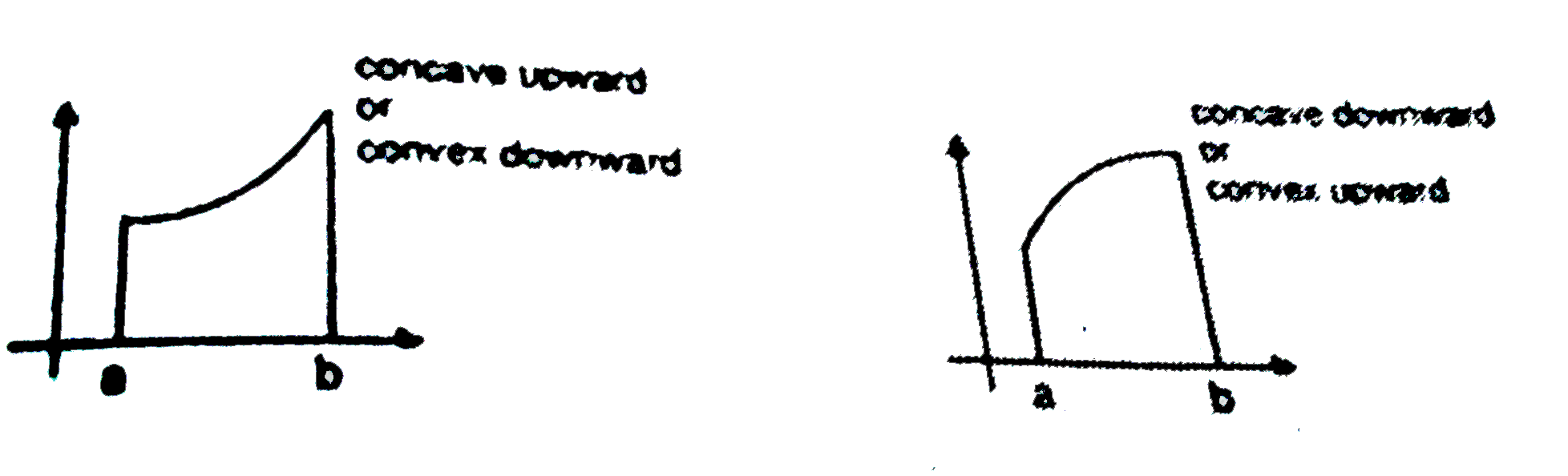
Inflection point :
The point where concavity of the curve changes is known as point of inflection (at inflection point f''(x) is equal to 0 or undefined)

Exhaustive set of values of 'a' for which the function f(x)=x4+ax3+3x22+1 will be concave upward along the entire real line is : (A) [−1,1] (B) [−2,2] (C) [0,2] (D) [0,4]
View SolutionFind the values of x for which the functions f(x)=3x2−1 and g(x)=3+x are equal
View SolutionFind the values of x for which the functions f(x)=3x2−1 and g(x)=3+x are equal
View SolutionFind the values of x for which the functions f(x)=3x2−1 and g(x)=3+x are equal
View SolutionThe number of integral values in the range of the function f(x)=sin−1x−cot−1x+x2+2x+6 is
View SolutionNumber of integral values of x satisfying function f(x)=log(x−1)+log(3−x)
View SolutionFind the number of integral vaues of 'a' for which the range of function f(x)=x2−ax+1x2−3x+2is (−∞,∞),
View SolutionThe number of integral values of a for which f(x)=x3+(a+2)x2+3ax+5 is monotonic in ∀x∈R
View SolutionFind the values 'a' for which the function f(x)=(a+2)x3−3ax2+9ax−1 decreases for all real values of x .
View SolutionFind the values of a for which the function f(x)=(a+2)x3−3ax2+9ax−1 decreasing for all real values of x.
View Solution
