the altitudes of are equal. Prove that is an equilateral triangle.
To prove that triangle ABC is an equilateral triangle given that the altitudes AD, BE, and CF are equal, we will follow these steps:
Step 1: Establish the Given Information
We know that AD, BE, and CF are the altitudes from vertices A, B, and C to the opposite sides BC, AC, and AB respectively, and that these altitudes are equal:
AD=BE=CF
Step 2: Consider Triangles BEC and BFC
We will analyze triangles BEC and BFC.
- Angle E and Angle F: Both angles are right angles (90 degrees) since they are altitudes.
- Side EC and Side FC: We are given that EC=FC (as they are segments of the equal altitudes).
- Side BC: The side BC is common to both triangles.
Step 3: Apply the RHS Criterion
Using the Right angle-Hypotenuse-Side (RHS) criterion for congruence, we can conclude:
△BEC≅△BFC
Step 4: Use CPCTC
From the congruence of triangles BEC and BFC, we can state:
∠B=∠C (by Corresponding Parts of Congruent Triangles are Congruent - CPCTC)
Step 5: Establish Relationship Between Sides
Since angles B and C are equal, the sides opposite these angles must also be equal:
AC=AB (sides opposite equal angles are equal)
Step 6: Consider Triangles ABD and ABE
Now, we will analyze triangles ABD and ABE.
- Angle D and Angle E: Both angles are right angles (90 degrees).
- Side AB: This side is common to both triangles.
- Side AD and Side BE: We are given that AD=BE (as they are equal altitudes).
Step 7: Apply the RHS Criterion Again
Using the RHS criterion again, we can conclude:
△ABD≅△ABE
Step 8: Use CPCTC Again
From the congruence of triangles ABD and ABE, we can state:
∠B=∠A (by CPCTC)
Step 9: Establish Relationship Between Sides Again
Since angles A and B are equal, the sides opposite these angles must also be equal:
AB=BC (sides opposite equal angles are equal)
Step 10: Conclude the Proof
Now we have:
1. AC=AB
2. AB=BC
From these, we can conclude:
AC=AB=BC
Thus, triangle ABC is an equilateral triangle.
We know that AD, BE, and CF are the altitudes from vertices A, B, and C to the opposite sides BC, AC, and AB respectively, and that these altitudes are equal:
AD=BE=CF
We will analyze triangles BEC and BFC.
- Side EC and Side FC: We are given that EC=FC (as they are segments of the equal altitudes).
- Side BC: The side BC is common to both triangles.
Using the Right angle-Hypotenuse-Side (RHS) criterion for congruence, we can conclude:
△BEC≅△BFC
From the congruence of triangles BEC and BFC, we can state:
∠B=∠C (by Corresponding Parts of Congruent Triangles are Congruent - CPCTC)
Since angles B and C are equal, the sides opposite these angles must also be equal:
AC=AB (sides opposite equal angles are equal)
Now, we will analyze triangles ABD and ABE.
- Side AB: This side is common to both triangles.
- Side AD and Side BE: We are given that AD=BE (as they are equal altitudes).
Using the RHS criterion again, we can conclude:
△ABD≅△ABE
From the congruence of triangles ABD and ABE, we can state:
∠B=∠A (by CPCTC)
Since angles A and B are equal, the sides opposite these angles must also be equal:
AB=BC (sides opposite equal angles are equal)
Now we have:
1. AC=AB
2. AB=BC
AC=AB=BC
Topper's Solved these Questions
Similar Questions
In Figure, BD and CE are two altitudes of a ABC such that BD=CE. Prove that ABC is isosceles.
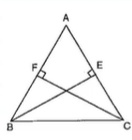 View Solution
View SolutionIn Figure ABCDandAEFD are two parallelograms. Prove that: PE=FQ
 View Solution
View SolutionIn Figure, AD and BE are medians of ABC and BE∣∣DF . Prove that CF=14AC
Consider △ABC Since AD is Median
⇒BD=BC⋯(1)
Since BE is Median⇒AE=EC⋯(2)
Consider △BECSince BE∣∣DF
By Basic Proportionality theorm, ⇒BDDC=EFFC
From (1)⇒CF=EF
⇒CF=12AE
From (2)⇒CF=14ACView SolutionFill the blanks in the following so that each of the following statements is true.
(i) Sides opposite to equal angles of a triangle are ......
(ii) Angle opposite to equal sides of a triangle are .....
(iii) In an equilateral triangle all angles are .....
(iv) In a ΔABC if ∠A = ∠C , then AB = ......
(v) If altitudes CE and BF of a triangle ABC are equal, then AB = ....
(vi) In an isosceles triangle ABC with AB = AC, if BD and CE are its altitudes, then BD is …… CE.
(vii) In right triangles ABC and DEF, if hypotenuse AB = EF and side AC = DE, then ΔABC ≅ Δ ……View SolutionThe sides AB and CD of a parallelogram ABCD are bisected at E and F. Prove that EBFD is a parallelogram.
View SolutionIn Figure, ABCD, ABFE and CDEF are parallelograms. Prove that ar(ADE)=ar(BCF)
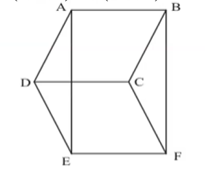 View Solution
View SolutionIn Figure, it is given that AB=BC and AD=EC . Prove that ABE≅CBD
 View Solution
View SolutionIn Fig. 4.101, AD and CE are two altitudes of ABC . Prove that AEF~CDF (ii) ABD~CBE (iii) AEF~ADB (iv) FDC~BEC (FIGURE)
View SolutionIn a ABC,EandF are the mid-points of ACandAB respectively. The altitude AP to BC intersects FE at Q Prove that AQ=QP
View SolutionABC is a triangle in which D is the mid-point of BC ,E andF are mid-points of DC and AE respectively. If area of ABC is 16cm2, find the area of DEF
View Solution

