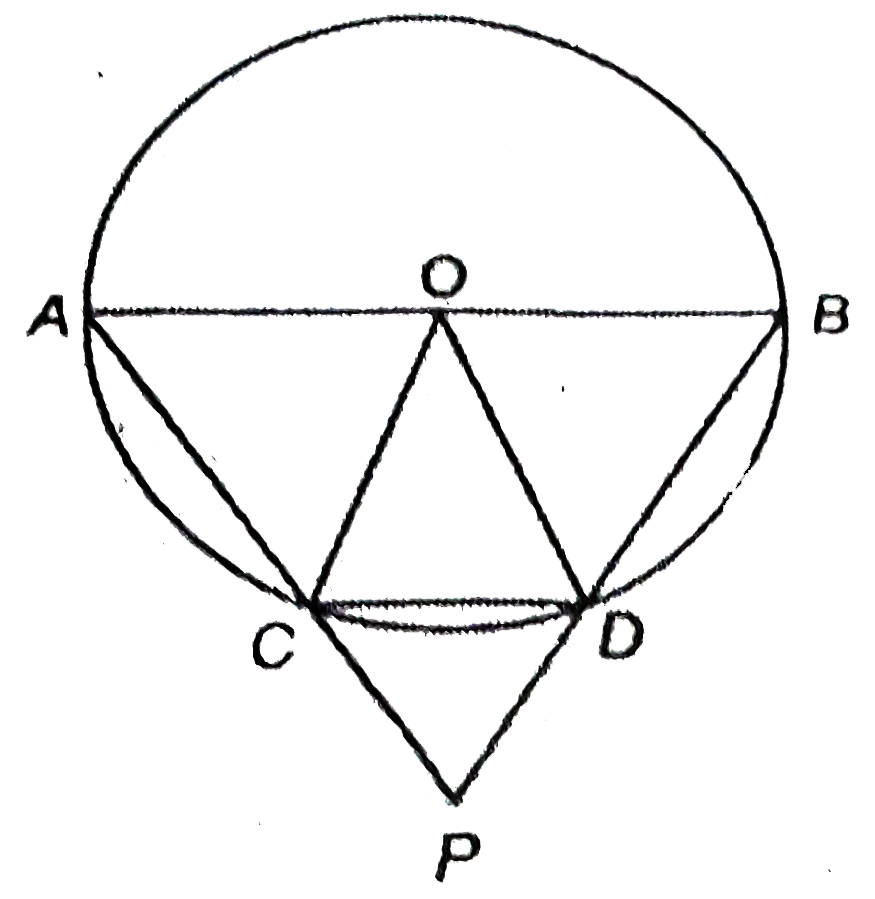
AB is diameter of a circle with centre 'O'. CD is a chord which is equal to the radius of the circle. AC and BD are extended so that they intersect each other at point P. Then find the value of ∠APB.
30∘
60∘
90∘
120∘
To solve the problem, we will follow these steps:
Step 1: Understand the Circle and Given Elements
We have a circle with center O and diameter AB. CD is a chord that is equal to the radius of the circle. We need to find the angle APB where AC and BD are extended to meet at point P.
Hint: Draw a diagram to visualize the circle, diameter, chord, and the extended lines.
Step 2: Identify the Lengths
Let the radius of the circle be denoted as R. Since CD is equal to the radius, we have:
- OC = OD = R (where O is the center of the circle).
Hint: Remember that in a circle, all radii are equal.
Step 3: Analyze Triangle OCD
Since OC and OD are both radii of the circle, triangle OCD is an isosceles triangle. Moreover, since CD = R, triangle OCD is also equilateral.
Hint: In an equilateral triangle, all sides are equal and all angles are 60 degrees.
Step 4: Calculate Angle DOC
In triangle OCD, since it is equilateral, we have:
- Angle DOC = 60 degrees.
Hint: Use the properties of equilateral triangles to find the angles.
Step 5: Extend Lines AC and BD
Now, we extend lines AC and BD to meet at point P. We need to find angle APB.
Hint: Remember that the angle at the center (angle DOC) relates to the angle at the circumference (angle APB).
Step 6: Relate Angle APB to Angle DOC
The angle at point P (angle APB) can be calculated using the following relationship:
- Angle APB = 90 degrees - (Angle DOC / 2).
Substituting the known value:
- Angle APB = 90 degrees - (60 degrees / 2)
- Angle APB = 90 degrees - 30 degrees
- Angle APB = 60 degrees.
Hint: This formula comes from the fact that the angle at the circumference is half of the angle at the center.
Conclusion
Thus, the value of angle APB is 60 degrees.
Final Answer: Angle APB = 60 degrees.
We have a circle with center O and diameter AB. CD is a chord that is equal to the radius of the circle. We need to find the angle APB where AC and BD are extended to meet at point P.
Let the radius of the circle be denoted as R. Since CD is equal to the radius, we have:
- OC = OD = R (where O is the center of the circle).
Since OC and OD are both radii of the circle, triangle OCD is an isosceles triangle. Moreover, since CD = R, triangle OCD is also equilateral.
In triangle OCD, since it is equilateral, we have:
- Angle DOC = 60 degrees.
Now, we extend lines AC and BD to meet at point P. We need to find angle APB.
The angle at point P (angle APB) can be calculated using the following relationship:
- Angle APB = 90 degrees - (Angle DOC / 2).
- Angle APB = 90 degrees - (60 degrees / 2)
- Angle APB = 90 degrees - 30 degrees
- Angle APB = 60 degrees.
Thus, the value of angle APB is 60 degrees.
Topper's Solved these Questions
Similar Questions
In a circle with centre O, AB is a diameter and CD is a chord which is equal to the radius OC. AC and BD are extended in such a way that they intersect each other at a point P, exterior to the circle. The measure of ∠APB is
View SolutionIn the adjoinig figure, AB is a diameter of the circle, CD is a chord equal to the radius of the circle. AC and BD when extended intersect at a point E. Prove that ∠AEB=60∘.
 View Solution
View Solution
Knowledge Check
- Question 1 - Select One
AB is a diameter of a circle with centre O. CD is a chord equal to the radius of the circle. AC and BD are produced to meet at P. Then the measure of ∠APB is:
A120∘B30∘C60∘D90∘ - Question 2 - Select One
AB is a diameter of the circle, CD is a chord equal to the radius of the circle. AC and BD when extended intersect at a point E. Find the ∠AEB.
A30∘B60∘C90∘D45∘ - Question 3 - Select One
In a circle with centre O, AB is a diameter and CD is a chord which is equal to the radius OC. AC and BD are extended in such a way that they intersect each other at a point P, exterior to the circle. The measure of ∠APB is
A30∘B45∘C60∘D90∘
In Fig. 10.32, AB is a diameter of the circle, CD is a chord equal to theradius of the circle. AC and BD when extended intersect at a point E. Prove that∠AEB = 60∘
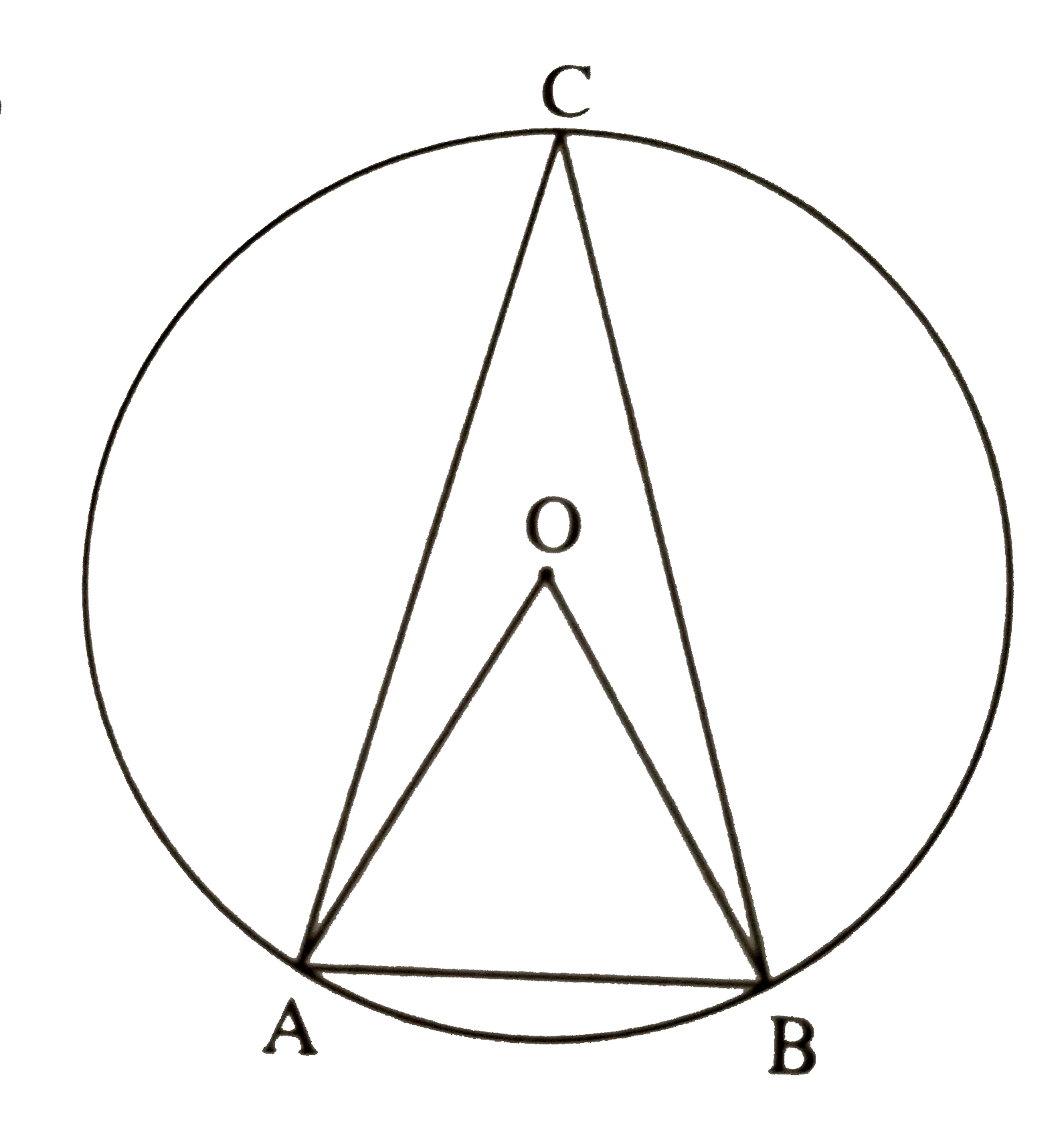
View SolutionIn the figure, in a circle with centre O, length of chord AB is equal to the radius of the circle. Find measure of each of the following.
∠AOB
 View Solution
View SolutionAB is a diameter of the circle with centre O and chord CD is equal to radius OC (fig). AC and BD proudced meet at P. Prove that ∠CPD=60∘.
 View Solution
View SolutionAB is a diameter of the circle with centre O, CD is chord of the circle. If ∠BOC=120∘, then the value of ∠ADC is
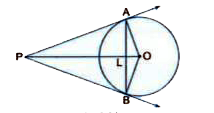
View SolutionIn Fig , AB is a chord of a circle , with centre O , such that AB = 16 cm and radius of circle is 10 cm. Tangents at A and B intersect each other at P . Find the length of PA.
 View Solution
View Solution

