AB is the diameter of a circle whose centre is O. DC is a chord of that circle. If DC||AB and ∠BAC=20∘ then ∠ADC=?
120∘
110∘
115∘
100∘
To solve the problem, we will follow these steps:
1. Draw the Circle and Label Points:
- Draw a circle with center O.
- Mark the diameter AB such that A and B are on the circle, and O is the midpoint of AB.
- Draw a chord DC such that DC is parallel to AB.
2. Identify Given Angles:
- We know that angle BAC = 20°.
3. Use Parallel Lines to Find Angle BDC:
- Since DC is parallel to AB and AB is a transversal line, angle BAC is equal to angle BDC (alternate interior angles).
- Therefore, angle BDC = 20°.
4. Identify Angle ADB:
- Since AB is the diameter of the circle, angle ADB (an angle inscribed in a semicircle) is equal to 90°.
5. Use the Cyclic Quadrilateral Property:
- Since ABCD is a cyclic quadrilateral, the sum of the opposite angles is 180°.
- Therefore, angle ADB + angle BDC = 180°.
- We already know angle ADB = 90° and angle BDC = 20°.
- Thus, angle ADC = 180° - angle BDC = 180° - 20° = 160°.
6. Calculate Angle ADC:
- Now, we need to find angle ADC. Since angle ADB = 90° and angle BDC = 20°, we can find angle ADC using the property of co-interior angles.
- Angle ADB + angle ADC = 180° (co-interior angles).
- Therefore, angle ADC = 180° - angle ADB = 180° - 90° = 90°.
7. Final Calculation:
- Since angle ADC is also equal to angle BDC + angle ADB, we can add them up:
- angle ADC = angle BDC + angle ADB = 20° + 90° = 110°.
Thus, the measure of angle ADC is 110°.
- Draw a circle with center O.
- Mark the diameter AB such that A and B are on the circle, and O is the midpoint of AB.
- Draw a chord DC such that DC is parallel to AB.
- We know that angle BAC = 20°.
- Since DC is parallel to AB and AB is a transversal line, angle BAC is equal to angle BDC (alternate interior angles).
- Therefore, angle BDC = 20°.
- Since AB is the diameter of the circle, angle ADB (an angle inscribed in a semicircle) is equal to 90°.
- Since ABCD is a cyclic quadrilateral, the sum of the opposite angles is 180°.
- Therefore, angle ADB + angle BDC = 180°.
- We already know angle ADB = 90° and angle BDC = 20°.
- Thus, angle ADC = 180° - angle BDC = 180° - 20° = 160°.
- Now, we need to find angle ADC. Since angle ADB = 90° and angle BDC = 20°, we can find angle ADC using the property of co-interior angles.
- Angle ADB + angle ADC = 180° (co-interior angles).
- Therefore, angle ADC = 180° - angle ADB = 180° - 90° = 90°.
- Since angle ADC is also equal to angle BDC + angle ADB, we can add them up:
- angle ADC = angle BDC + angle ADB = 20° + 90° = 110°.
Topper's Solved these Questions
Similar Questions
Knowledge Check
- Question 1 - Select One
In figure, if PQR is the tangent to a circle at Q whose centre is O, AB is a chord parallel to PR and ∠BQR=70∘ then ∠AQB is equal to
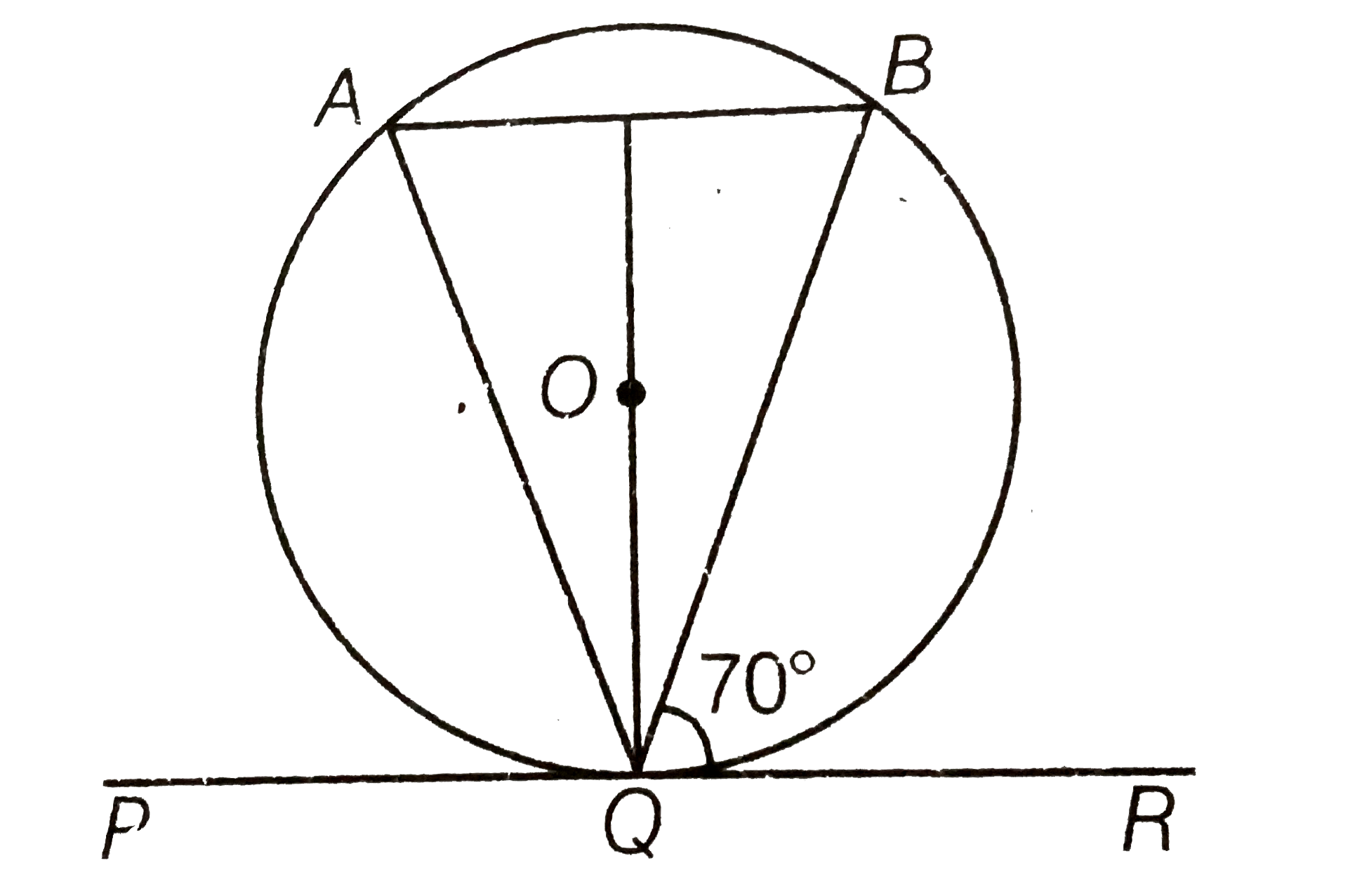 A20∘B40∘C35∘D45∘
A20∘B40∘C35∘D45∘ - Question 2 - Select One
AB is a diameter of the circle with centre O, CD is chord of the circle. If ∠BOC=120∘, then the value of ∠ADC is
A42∘B30∘C60∘D35∘ - Question 3 - Select One
AB is a diameter of a circle with centre O. CD is a chord equal to the radius of the circle. AC and BD are produced to meet at P. Then the measure of ∠APB is:
A120∘B30∘C60∘D90∘
In the figure given below, AB is the diameter of the circle whose centre is at O. Given that ∠ECD=∠EDC=32∘, then ∠CEFand∠COF respectively are
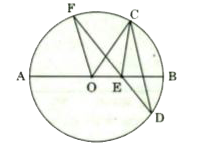 View Solution
View SolutionA diameter of a circle is a chord that………the centre.
View SolutionAB is a diameter of circle with centre O. PQ is a chord which do not cut AB. If AP and BQ are joined. If ∠BAP=∠ABQ then ABQP is-
View SolutionIn a circle with the centre is O and AB is the diameter of the circle and CD is the chord of the circle. If angle ABC is 54∘ and the length of CD and BC is equal, then find the ∠DBC.
View SolutionAB is a diameter of a circle with centre O, and P is a point on the circle. If ∠POA=130∘, the ∠PBO is equal to:
AB केंद्र O के साथ एक वृत्त पर एक व्यास है, और P वृत्त का एक बिंदु है। यदि ∠POA=130∘, तो ∠PBO का मान ज्ञात करे|View Solution

