If the coefficient of friction between the wedge A and block B shown in the figure is $μ$ , then the maximum possible horizontal acceleration of A for which B doesn’t slip is [ angle of inclination of wedge = $45^{\circ}$ ]

$μ g$

$g (\frac{1 + μ}{1 - μ})$

$\frac{g}{μ}$

$g (\frac{1 - μ}{1 + μ})$

Video Solution

Text Solution

Verified by Experts

The correct Answer is:B

Answer

Step by step video & image solution for If the coefficient of friction between the wedge A and block B shown in the figure is mu, then the maximum possible horizontal acceleration of A for which B doesn’t slip is [ angle of inclination of wedge = 45^@ ] by Physics experts to help you in doubts & scoring excellent marks in Class 12 exams.

Updated on:21/07/2023

Class 12 PHYSICS QUESTION BANK

Topper's Solved these Questions

Knowledge Check

Question 1 - Select One
If the coefficient of friction between $A$ and $B$ is $μ$ , the maximum acceleration of the wedge $A$ for which $B$ will remain at rest with respect to the wedge is

A $μ g$
B $g (\frac{1 + μ}{1 - μ})$
C $g (\frac{1 - μ}{1 + μ})$
D $\frac{g}{μ}$
Question 2 - Select One

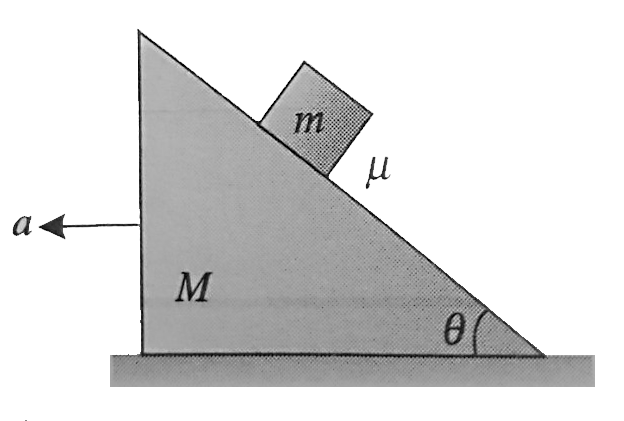
A block of mass m is at rest relative to the stationary wedge of mass M. The coefficient of friction between block and wedge is $μ$ . The wedge is now pulled horizontally with acceleration a as shown in figure. Then the minimum magnitude of a for the friction between block and wedge to be zero is:
A $> a n θ$
B $μ > a n θ$
C $g cot θ$
D $μ g cot θ$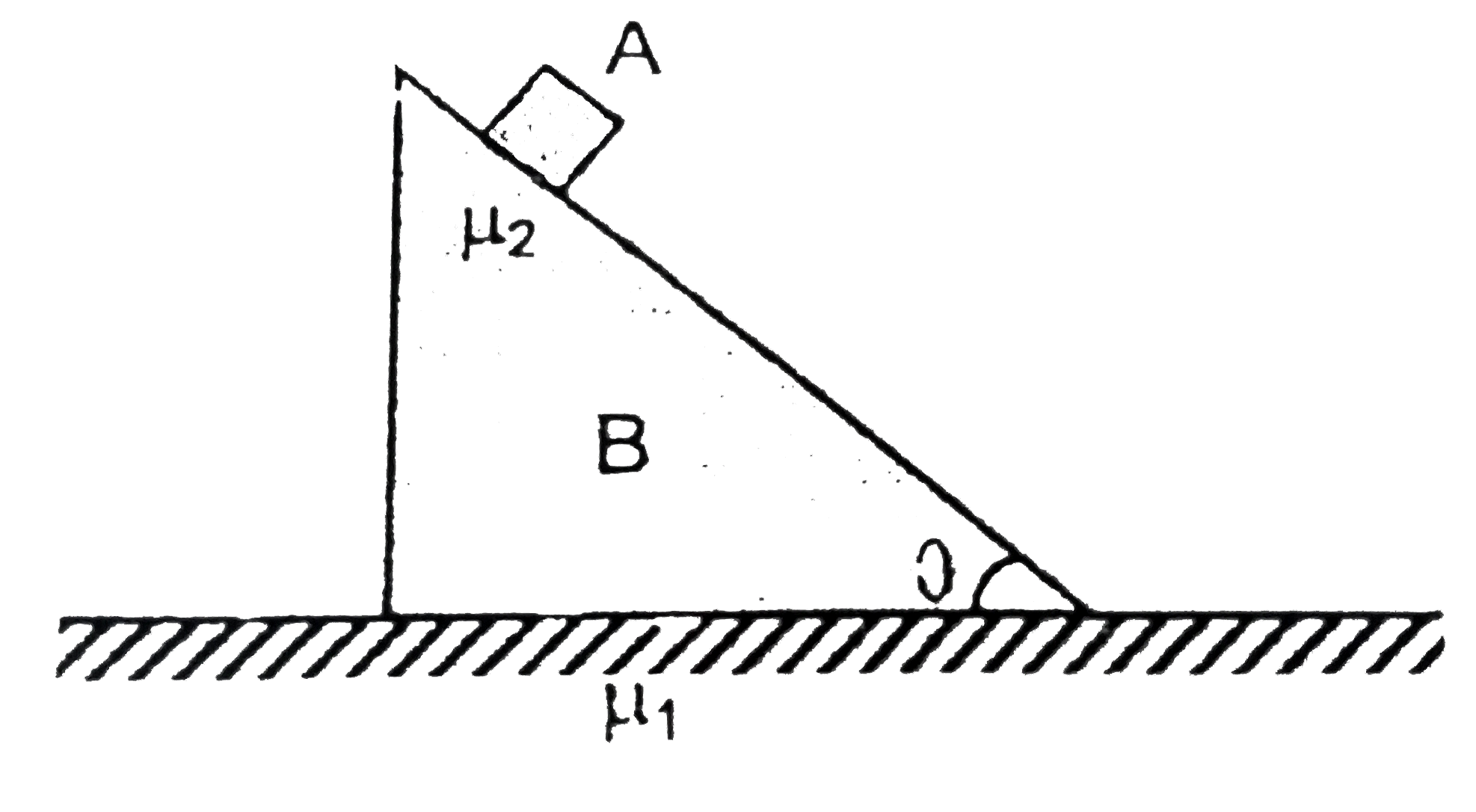
Question 3 - Select One or More

A wedge $B$ of mass 2 m is placed on a rough horizontal suface. The coefficient of friction between wedge and the horizontal surface is $μ_{1}$ . A block of mass m is placed on wedge as shown in the figure. The coefficient of friction between block and wedge is $μ_{2}$ . The block and wedge are released from rest.
Q. Suppose the inclined surface of the wedge is at $θ = 37^{\circ}$ from angle from horizontal and $μ_{2} = 0$ are wedge will remain in equilibrium if
A $μ_{1} = 0.1$
B $μ_{1} = 0.2$
C $μ_{1} = 0.3$
D $μ_{1} = 0.4$

NTA MOCK TESTS-NTA NEET SET 78-PHYSICS

Home
Ask Doubt
Profile

If the coefficient of friction between the wedge A and block B shown in the figure is μ, then the maximum possible horizontal acceleration of A for which B doesn’t slip is [ angle of inclination of wedge = 45∘ ]

The correct Answer is:B

Topper's Solved these Questions

Similar Questions

Knowledge Check

If the coefficient of friction between A and B is μ, the maximum acceleration of the wedge A for which B will remain at rest with respect to the wedge is

A block of mass m is at rest relative to the stationary wedge of mass M. The coefficient of friction between block and wedge is μ. The wedge is now pulled horizontally with acceleration a as shown in figure. Then the minimum magnitude of a for the friction between block and wedge to be zero is:

NTA MOCK TESTS-NTA NEET SET 78-PHYSICS

If the coefficient of friction between the wedge A and block B shown in the figure is $μ$ , then the maximum possible horizontal acceleration of A for which B doesn’t slip is [ angle of inclination of wedge = $45^{\circ}$ ]

If the coefficient of friction between $A$ and $B$ is $μ$ , the maximum acceleration of the wedge $A$ for which $B$ will remain at rest with respect to the wedge is

A block of mass m is at rest relative to the stationary wedge of mass M. The coefficient of friction between block and wedge is $μ$ . The wedge is now pulled horizontally with acceleration a as shown in figure. Then the minimum magnitude of a for the friction between block and wedge to be zero is: