Three point charges of +2q,+2qand−4q are placed at the corners A, B and C of an equilateral triangle ABC of side x. The magnitude of the electric dipole moment of this system is
2qx
3√2qx
3qx
2√3qx
The correct Answer is:D
To find the magnitude of the electric dipole moment of the system with charges +2q,+2q, and −4q placed at the corners of an equilateral triangle ABC with side length x, we can follow these steps:
1. Identify the Charges and Their Positions:
- Let charge +2q be at point A.
- Let charge +2q be at point B.
- Let charge −4q be at point C.
- The triangle ABC is equilateral with each side of length x.
2. Understanding the Dipole Moment:
- The electric dipole moment →p for a system of charges is given by the formula:
→p=∑→riqi
- Here, →ri is the position vector of the charge qi.
3. Calculate the Dipole Moment for Each Pair:
- We can consider the dipole moments created by the two +2q charges and the −4q charge.
- The dipole moment →p1 due to the charge at A and the charge at C:
→p1=(2q)(→rA−→rC)
- The dipole moment →p2 due to the charge at B and the charge at C:
→p2=(2q)(→rB−→rC)
4. Magnitude of Each Dipole Moment:
- The distance between charges A and C (or B and C) is x.
- Therefore, the magnitudes of →p1 and →p2 can be expressed as:
p1=2q⋅xandp2=2q⋅x
5. Net Dipole Moment Calculation:
- Since the angle between p1 and p2 in an equilateral triangle is 60∘, we can use the formula for the resultant of two vectors:
pnet=√p21+p22+2p1p2cos(60∘)
- Substituting cos(60∘)=12:
pnet=√(2qx)2+(2qx)2+2(2qx)(2qx)(12)
- Simplifying this:
pnet=√4q2x2+4q2x2+2q2x2=√10q2x2=√10qx
6. Final Result:
- The magnitude of the electric dipole moment of this system is:
pnet=√3⋅2qx=2√3qx
- Let charge +2q be at point A.
- Let charge +2q be at point B.
- Let charge −4q be at point C.
- The triangle ABC is equilateral with each side of length x.
- The electric dipole moment →p for a system of charges is given by the formula:
→p=∑→riqi
- Here, →ri is the position vector of the charge qi.
- We can consider the dipole moments created by the two +2q charges and the −4q charge.
- The dipole moment →p1 due to the charge at A and the charge at C:
→p1=(2q)(→rA−→rC)
- The dipole moment →p2 due to the charge at B and the charge at C:
→p2=(2q)(→rB−→rC)
- The distance between charges A and C (or B and C) is x.
- Therefore, the magnitudes of →p1 and →p2 can be expressed as:
p1=2q⋅xandp2=2q⋅x
- Since the angle between p1 and p2 in an equilateral triangle is 60∘, we can use the formula for the resultant of two vectors:
pnet=√p21+p22+2p1p2cos(60∘)
- Substituting cos(60∘)=12:
pnet=√(2qx)2+(2qx)2+2(2qx)(2qx)(12)
- Simplifying this:
pnet=√4q2x2+4q2x2+2q2x2=√10q2x2=√10qx
- The magnitude of the electric dipole moment of this system is:
pnet=√3⋅2qx=2√3qx
Topper's Solved these Questions
Similar Questions
Electric charges q,q,–2q are placed at the corners of an equilateral triangle ABC of side l. The magnitude of electric dipole moment of the system is
View SolutionElectric charges -q -q -q and 3q are placed at the corners of a square ABCD of length 1 as shown in figure.The magnitude of electric dipole moment of the system is
View Solution
Knowledge Check
Electric charges q,q,–2q are placed at the corners of an equilateral triangle ABC of side l. The magnitude of electric dipole moment of the system is
AqLB2qLC√3gLD4qLEqual charges q are placed at the vertices A and B of an equilatral triangle ABC of side a. The magnitude of electric field at the point C is
Aq4πε0a2B√2q4πε0a2C√3q4πε0a2Dq2πε0a2Three charges of (+2q),(−q) and (−q) are placed at the corners A,B and C of an equilateral triangle of side a as shown in the adjoining figure. Then the dipole moment of this combination is
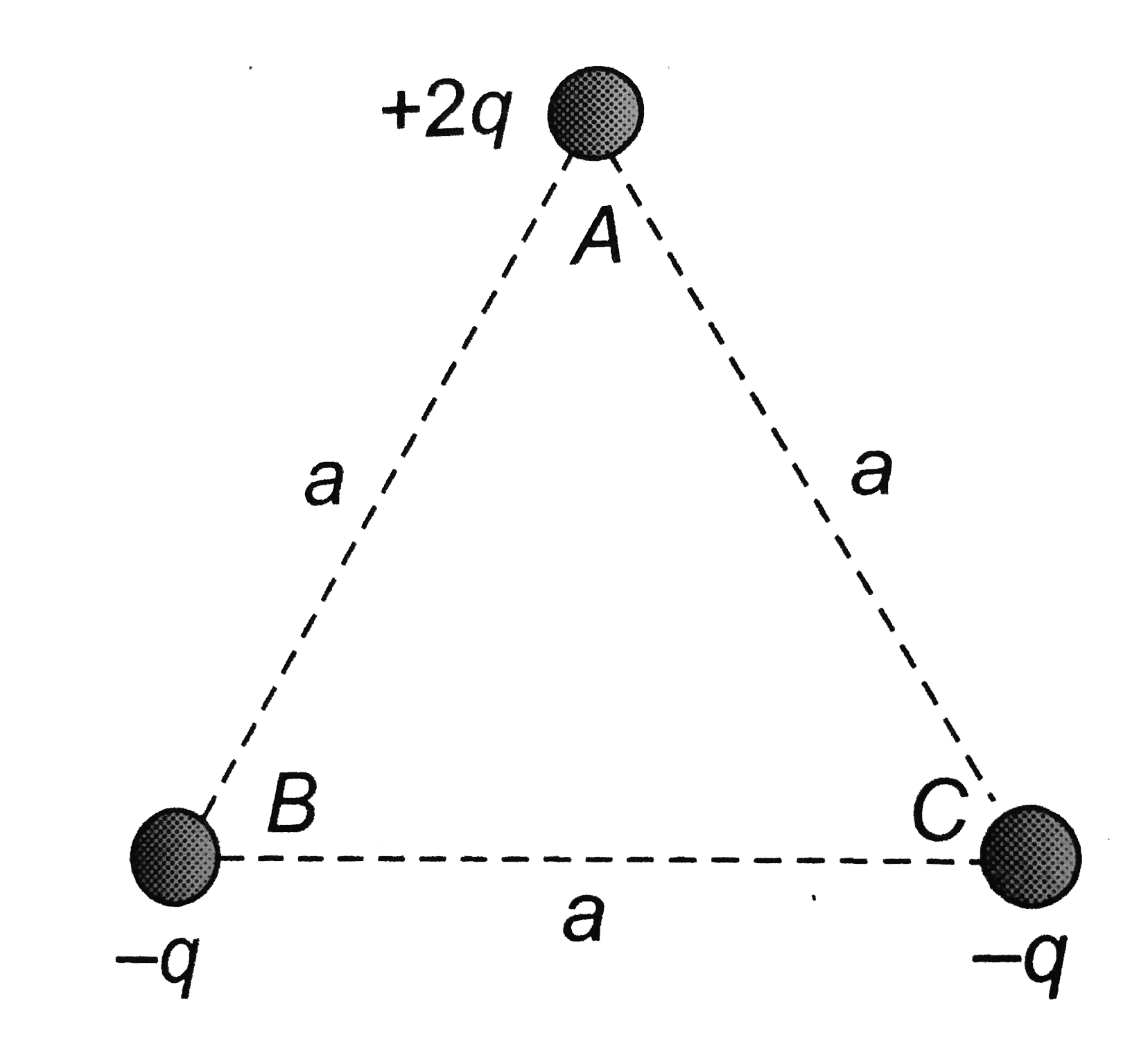 AqaBZeroCqa√3D2√3qa
AqaBZeroCqa√3D2√3qa
Three charges +q,+qand−q are located at the corners of an equilaterial triangle of side a. Calculate potential energy of the system.
View SolutionThree point charges q,−4q and 2q are placed at the vertices of an equilateral triangle ABC of side 'l' as shown in the Fig. Obtain the experssion for the magnitude of the resultant electric force acting on the charge q.
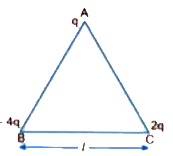
View SolutionElectric charges q,q,2q are placed at the equilateral triangle ABC of side l .The electric dipole moment of the system is ?
View SolutionThree charges +Q each are placed at the corners A,B and C of an equilateral triangle. At the circumcenre, O the electric field wil be

View SolutionThree charges 2q,−q,and−q are located at the vertices of an equilateral triangle. At the center of the triangle,
View Solution
