Electric charges q,q,2q are placed at the equilateral triangle ABC of side l .The electric dipole moment of the system is ?
√3ql
√2ql
ql
2ql
The correct Answer is:A
To find the electric dipole moment of the system with charges q,q, and 2q placed at the vertices of an equilateral triangle ABC with side length l, we can follow these steps:
1. Identify the Charges and Their Positions:
- Let the charges be placed as follows:
- Charge q at vertex A,
- Charge q at vertex B,
- Charge 2q at vertex C.
- The vertices A, B, and C form an equilateral triangle with side length l.
2. Calculate the Dipole Moment for Each Pair:
- The electric dipole moment →p is defined as:
→p=q⋅→d
where →d is the vector pointing from the negative charge to the positive charge.
- We will calculate the dipole moments for the pairs (A, C) and (B, C).
3. Calculate Dipole Moment →p1 for Pair (A, C):
- For the pair (A, C):
- Charge at A is q (positive),
- Charge at C is 2q (negative).
- The distance d between A and C is l.
- The dipole moment →p1 is given by:
→p1=2q⋅l2=ql(acting from C to A)
4. Calculate Dipole Moment →p2 for Pair (B, C):
- For the pair (B, C):
- Charge at B is q (positive),
- Charge at C is 2q (negative).
- The distance d between B and C is also l.
- The dipole moment →p2 is given by:
→p2=2q⋅l2=ql(acting from C to B)
5. Resultant Dipole Moment:
- The angle between →p1 and →p2 is 60∘ because of the equilateral triangle.
- Using the formula for the resultant of two vectors:
pnet=√p21+p22+2p1p2cos(60∘)
- Since p1=p2=p:
pnet=√p2+p2+2p2⋅12=√2p2+p2=√3p2=√3p
6. Substituting the Value of p:
- We have p=ql, so:
pnet=√3⋅ql
Final Answer:
The electric dipole moment of the system is:
→pnet=√3ql
- Let the charges be placed as follows:
- Charge q at vertex A,
- Charge q at vertex B,
- Charge 2q at vertex C.
- The vertices A, B, and C form an equilateral triangle with side length l.
- The electric dipole moment →p is defined as:
→p=q⋅→d
where →d is the vector pointing from the negative charge to the positive charge.
- We will calculate the dipole moments for the pairs (A, C) and (B, C).
- For the pair (A, C):
- Charge at A is q (positive),
- Charge at C is 2q (negative).
- The distance d between A and C is l.
- The dipole moment →p1 is given by:
→p1=2q⋅l2=ql(acting from C to A)
- For the pair (B, C):
- Charge at B is q (positive),
- Charge at C is 2q (negative).
- The distance d between B and C is also l.
- The dipole moment →p2 is given by:
→p2=2q⋅l2=ql(acting from C to B)
- The angle between →p1 and →p2 is 60∘ because of the equilateral triangle.
- Using the formula for the resultant of two vectors:
pnet=√p21+p22+2p1p2cos(60∘)
- Since p1=p2=p:
pnet=√p2+p2+2p2⋅12=√2p2+p2=√3p2=√3p
- We have p=ql, so:
pnet=√3⋅ql
The electric dipole moment of the system is:
→pnet=√3ql
Topper's Solved these Questions
- ELECTRIC CHARGES AND FIELDS Book:PHYSICS WALLAHChapter:ELECTRIC CHARGES AND FIELDS Exercise:NEET PAST 5 YEARS QUESTIONS
Explore 7 Videos
- ELECTRIC CHARGES AND FIELDS Book:PHYSICS WALLAHChapter:ELECTRIC CHARGES AND FIELDS Exercise:NEET PAST 5 YEARS QUESTIONS
Explore 7 Videos
- DUAL NATURE OF RADIATION AND MATTERBook:PHYSICS WALLAHChapter:DUAL NATURE OF RADIATION AND MATTERExercise:Neet past 5 years questions
Explore 16 Videos
- ELECTROMAGNETIC INDUCTION Book:PHYSICS WALLAHChapter:ELECTROMAGNETIC INDUCTION Exercise:NEET PAST 5 YEARS QUESTIONS
Explore 10 Videos
Similar Questions
Electric charges q,q,–2q are placed at the corners of an equilateral triangle ABC of side l. The magnitude of electric dipole moment of the system is
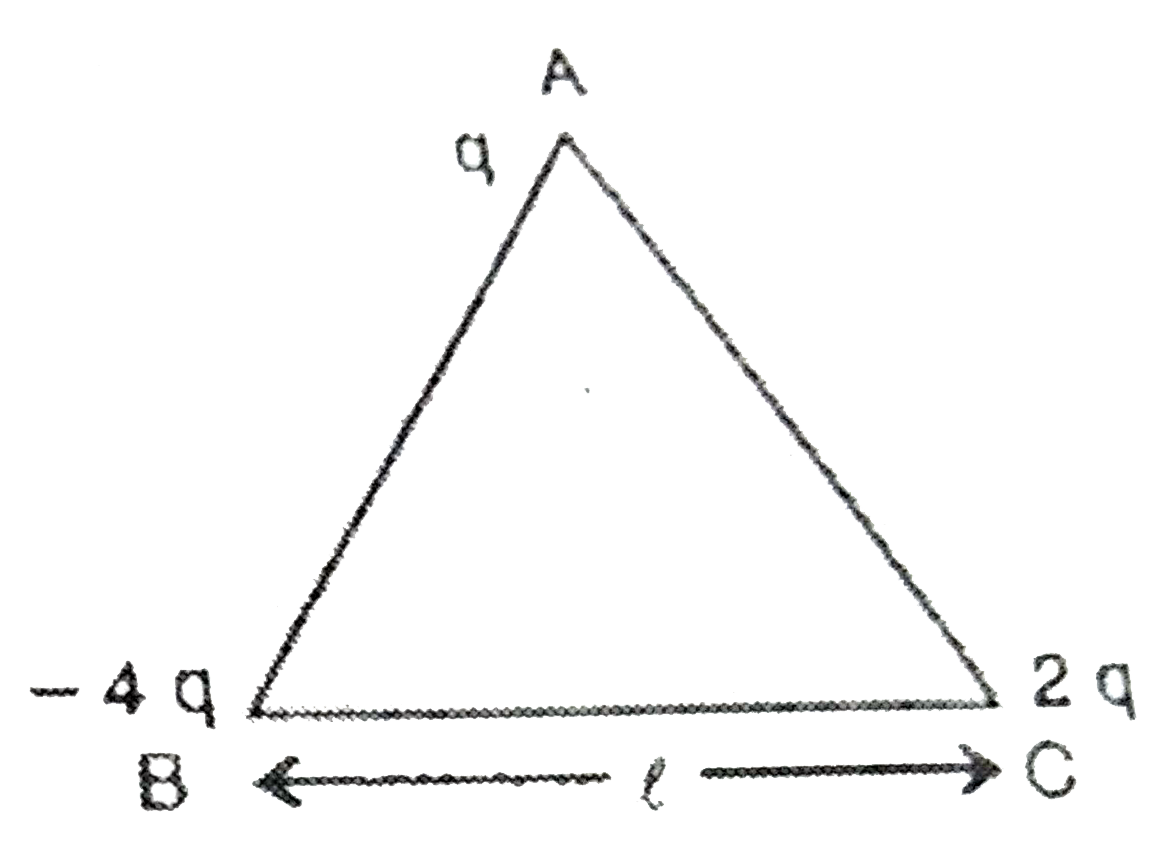
View Solution(a) Three point charges q,-4q and 2q are placed at the vertices of an equilateral triangle ABC of side 'l' as shown in the figure. Obtain the expression for the magnitude of the resultant electric force acting on the charge q.
(b) Find out the amount of the work done to separate the charges at infinite distance.
View Solution
Knowledge Check
Electric charges q,q,–2q are placed at the corners of an equilateral triangle ABC of side l. The magnitude of electric dipole moment of the system is
AqLB2qLC√3gLD4qLThree point charges of +2q,+2qand−4q are placed at the corners A, B and C of an equilateral triangle ABC of side x. The magnitude of the electric dipole moment of this system is
A2 qxB3√2qxC3 qxD2√3qxThree point charges of +2q,+2qand−4q are placed at the corners A, B and C of an equilateral triangle ABC of side x. The magnitude of the electric dipole moment of this system is
A2qxB3√2qxC3qxD2√3qx
Three point masses each of mass m are placed at the corners of an equilateral triangle of side 'a' . Then the moment of inertia of this system about an axis passing along one side of the triangle is
View SolutionThree point charges are kept at the three corners of an equilateral triangle of edge length a, as shown in the figure. The net electric dipole moment of the system is

View Solution(a) Three point charges q,-4q and 2q are placed at the vertices of an equilateral triangle ABC of side 'l' as shown in the figure. Obtain the expression for the magnitude of the resultant electric force acting on the charge q.
(b) Find out the amount of the work 4one to separate the charges at infinite distance.

View SolutionThree charges +q, +q and -2q are placed at the vertices of an equilareral triagle. What is the dipole moment of the system?
View SolutionThree charge −q,+q and −q are placed at the cornors of an equilateral triangle of side a The resultant electric froce an a charge +q placed at a the centroid O of the triangle is
View Solution
