Four particles, each of mass m and charge q, are held at the vertices of a square of side 'a'. They are released at t = 0 and move under mutual repulsive forces speed of any particle when its distance from the centre of square doubles is
[14πε0q2ma(1+12√2)]1/2
[14πε0q2ma]1/2
[14πε0q2ma2]1/2
[14πε0q2ma2(1+12√2)]1/2
The correct Answer is:A
Step by step video & image solution for Four particles, each of mass m and charge q, are held at the vertices of a square of side 'a'. They are released at t = 0 and move under mutual repulsive forces speed of any particle when its distance from the centre of square doubles is by Physics experts to help you in doubts & scoring excellent marks in Class 12 exams.
Topper's Solved these Questions
Similar Questions
Knowledge Check
- Question 1 - Select One
Four particles each of mass m are placed at the vertices of a square of side l. the potential at the centre of square is
A−2√2GmlB−3√2GmlC−2GmlD−4√2Gml - Question 2 - Select One
Find the potential energy of 4-particles, each of mass 1 kg placed at the four vertices of a square of side length 1 m.
A+4.0GB7.5GC−5.4GD+6.3G - Question 3 - Select One
Find the gravitational potential energy of a system of four particles, each of mass m placed at the verticles of a square of side l. Also obtain the gravitaitonal potential at centre of the square.
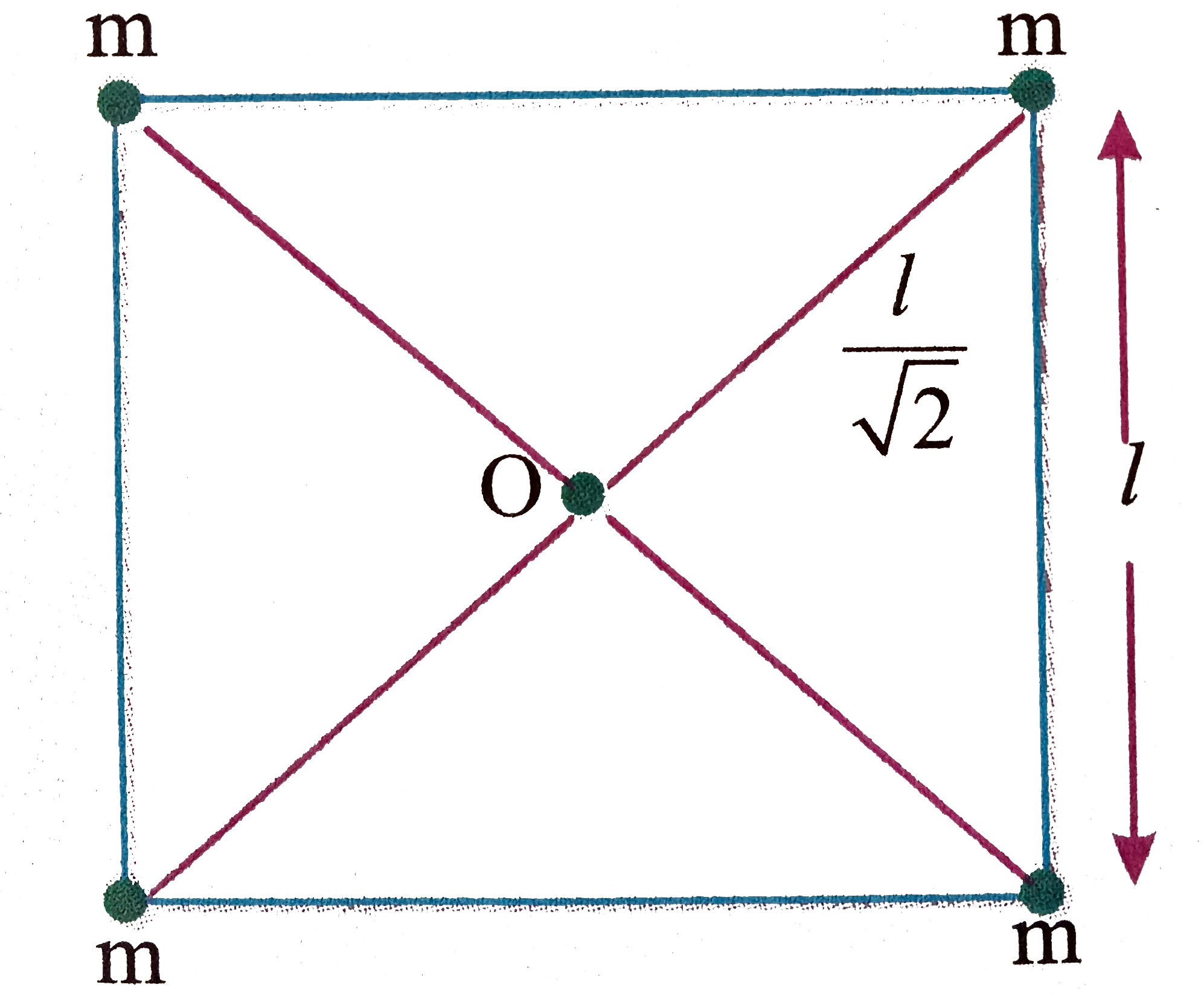 A−√32GMLB−√64GML2CzeroD−√16GML
A−√32GMLB−√64GML2CzeroD−√16GML
Four particle each of mass 1kg are at the four orners of a square of side 1m . The work done to move one of the particles to infinity
View SolutionFour particles of masses m, m, 2m and 2m are placed at the four corners of square of side a. Find the centre of mass of the system.
View SolutionFour particles of masses m, m, 2m and 2m are placed at the corners of a square of side a, as shown in fig. Locate the centre of mass.
View SolutionFour equal masses (each of mass M) are placed at the corners of a square of side a. The escape velocity of a body from the centre O of the square is
View SolutionA, B, C and D are four particles with each of mass M lying on the vertices of a square of side a. They always move along a common circle with velocity v under mutual gravitational force. Find v so that they always remain on the vertices of the square
View Solution

