An ideal gas is enclosed in a vertical cylindrical container and supports a freely moving piston of mass M. The piston and the cylinder have an equal cross-sectional area A. Atmospheric pressure is p0 and when the piston is in equilibrium, the volume of the gas is V0. The piston is now displaced slightly from its equilibrium position. Assuming that the system, is completely isolated from, its surroundings, what is the frequency of oscillation.
f=12π√γ(p0A2+MgA)V0M
f=12π√1γ(p0A2+MgA)V0M
f=12π√(p0A2+MgA)V0M
f=12π√A(p0A2+MgA)V0M
The correct Answer is:A
To find the frequency of oscillation of the piston in the given system, we can follow these steps:
Step 1: Understand the equilibrium condition
At equilibrium, the forces acting on the piston are balanced. The upward force due to the gas pressure (P1) and the atmospheric pressure (P0) must equal the downward force due to the weight of the piston (Mg).
P1A=P0A+Mg
Step 2: Displace the piston
When the piston is displaced by a small distance x, the pressure inside the cylinder changes. The new pressure can be expressed as:
P=P1+ΔP
where ΔP is the change in pressure due to the displacement.
Step 3: Apply the force balance after displacement
The net force acting on the piston after displacement can be expressed as:
Fnet=(P1+ΔP)A−P0A−Mg
This can be simplified to:
Fnet=ΔPA
Step 4: Relate pressure change to volume change
Using the adiabatic condition for an ideal gas, we know that:
PVγ=constant
Differentiating this gives us:
ΔP=−γPVΔV
The change in volume ΔV can be expressed as A⋅x, where x is the displacement of the piston. Thus,
ΔP=−γP1AV0x
Step 5: Substitute ΔP into the force equation
Substituting ΔP into the net force equation gives:
Fnet=−γP1A2V0x
Using Newton's second law, F=ma, we have:
Md2xdt2=−γP1A2V0x
Step 6: Identify the form of simple harmonic motion
This equation resembles the standard form of simple harmonic motion:
d2xdt2+ω2x=0
where ω2=γP1A2MV0.
Step 7: Find the frequency of oscillation
The frequency f is related to ω by:
ω=2πf
Thus, we can express the frequency as:
f=12π√γP1A2MV0
Step 8: Final expression for frequency
Substituting back into the equation, we find:
f=12π√γ(Mg+P0A)MV0
This gives us the frequency of oscillation of the piston.
At equilibrium, the forces acting on the piston are balanced. The upward force due to the gas pressure (P1) and the atmospheric pressure (P0) must equal the downward force due to the weight of the piston (Mg).
When the piston is displaced by a small distance x, the pressure inside the cylinder changes. The new pressure can be expressed as:
The net force acting on the piston after displacement can be expressed as:
Using the adiabatic condition for an ideal gas, we know that:
Substituting ΔP into the net force equation gives:
This equation resembles the standard form of simple harmonic motion:
The frequency f is related to ω by:
Substituting back into the equation, we find:
Topper's Solved these Questions
Similar Questions
An ideal gas enclosed in a cylindrical container supports a freely moving piston of mass M. The piston and the cylinder have equal cross-sectional area A. When the piston is in equilibrium, the volume of the gas is V0 and its pressure is P0. The piston is slightly displaced from the equilibrium position and released. Assuming that the system is completely isolated from its surrounding, the piston executes a simple harmonic motion with frequency
View SolutionAn ideal gas enclosed in a cylindrical container supports a freely moving piston of mass M. The piston and the cylinder have equal cross-sectional area A. When the piston is in equilibrium, the volume of the gas is V0 and its pressure is P0. The piston is slightly displaced from the equilibrium position and released. Assuming that the system is completely isolated from its surrounding, the piston executes a simple harmonic motion with frequency
View Solution
Knowledge Check
An ideal gas enclosed in a vertical cylindrical container supports a freely moving pistion of mass M. The pistion and the cylinder have equal cross sectional area A. When the pistion is in equilibrium, the volume of the gas is V0 and its pressure is P0. The pistion is slightly displaced from the equilibrium position and released. Assuming that the system is completely isolated from its surrounding, the pistion executes a simple harmonic motion with frequency
A12πAγP0V0MB12πV0MP0A2γC12π√A2γP0MV0D12π√MV0AγP0An ideal gas enclosed in a cylindrical container supports a freely moving piston of mass M. The piston and the cylinder have equal cross-sectional area A. When the piston is in equilibrium, the volum of the gas is V0 and its pressur is P0. The pistong is slightly displaced from the equilibrium position and released. Assuming that the system is completely isolated from its surrounding, the piston executes a simple harmonic motion with frequency
A12πγAP0V0MB12πV0MP0γA2C12π√γA2P0MV0D12π√MV0γ2P0A gas is contained in a metallic cylinder fitted with a piston.the piston is suddenly moved in to compress the gas and is maintained at this position. As time passes the pressure of the gas in the cylinder
AincreaseBdecreaseCremains constantDincrease or decrease depending on the nature of the gas.
A cylidrical vesel containing a liquid is closed by a smooth piston of mass m as shown in the figure. The area of cross section of the piston is A. If the atmospheric pressure is P0, find the pressure of the liquid just below the piston.
 ,
,
View SolutionA cylinderical vessel contaning liquid is closed by a smooth piston of mass m. the area of cross-section of the piston is A. if the atmospheric pressure is P0, Find the pressure of the liquid just below the piston.
View SolutionAn ideal gas is enclosed in a cylinder having cross sectional area A. The piston of mass M has its lower face inclined at θ to the horizontal. The lower face of the piston also has a hemispherical bulge of radius r. The atmospheric pressure is P0.
(a) Find pressure of the gas.
(b) The piston is slowly pulled up by a distance x. During the process the piston is always maintained in equilibrium by adding heat to the gas. [It means if the piston is left at any stage it will stay there in equilibrium]. Find change in temperature of the gas. Number of mole of the gas in the cylinder is one.

View SolutionA cylindrical vessel containing a liquid is closed by a smooth piston of mass "100g" as shown in the figure.The radius of the piston is "10cm" .If the atmospheric pressure is P0 then the pressure difference of the liquid just below the piston and the atmospheric pressure is (g=10ms2)
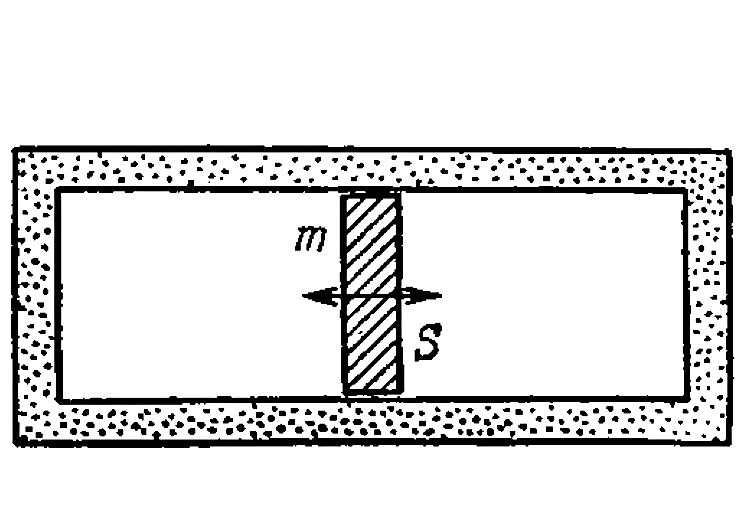
View SolutionIn a cylinder filled up with ideal gas end gas and closed from both ends there is a piston of mass m and cross − sectional area S (figure).In equilibrium the piston divides the cylinder into two equal parts, each with volime V0 . The gas ppressure is p0. The piston was slightly displaced from the equlibrium position and released.Find the oscillation frequency, assuming the prosecces in the gas to be adiabatic and the friction negligible.
View Solution
