The complex that exists as a pair of enantiomers is
trans −[Co(H2NCH2CH2NH2)2Cl2]+
cis−[Co(NH3)4Cl2]+
[Pt(PPh3)(Cl)(Br)(CN)]−
[Co(H2NCH2CH2NH2)3]3+
The correct Answer is:D
To determine the complex that exists as a pair of enantiomers, we need to follow these steps:
Step 1: Understand Enantiomers
Enantiomers are pairs of molecules that are non-superimposable mirror images of each other. This means that if you were to place one molecule over its mirror image, they would not align perfectly.
Hint: Remember that enantiomers must lack a plane of symmetry.
Step 2: Identify the Complexes
We need to analyze the given options to see which complex can form enantiomers. The options provided are:
1. Trans (CoCl2(en))
2. Cis (CoCl2(en))
3. Square planar (Pt(PPh3)(Cl)(Br)(CN))
4. Octahedral (Co(en)3)3+
Hint: Look for complexes that have chiral centers or lack a plane of symmetry.
Step 3: Analyze Each Option
1. Trans (CoCl2(en)): In this complex, the two chloride ligands are positioned opposite each other (180 degrees apart). This arrangement allows for a plane of symmetry, making it optically inactive and therefore not capable of forming enantiomers.
Hint: Check if the ligands are arranged in a way that creates symmetry.
2. Cis (CoCl2(en)): In this complex, the two chloride ligands are adjacent to each other. This arrangement does not allow for a plane of symmetry, resulting in the potential for non-superimposable mirror images, thus forming enantiomers.
Hint: Look for arrangements where ligands are not symmetrically placed.
3. Square planar (Pt(PPh3)(Cl)(Br)(CN)): This complex is square planar and has a symmetrical arrangement of ligands. It also possesses a plane of symmetry, making it optically inactive and not capable of forming enantiomers.
Hint: Visualize the structure to see if it can be divided into two identical halves.
4. Octahedral (Co(en)3)3+: This complex consists of three bidentate ethylenediamine (en) ligands. The arrangement of these ligands can lead to non-superimposable mirror images, indicating that it can form enantiomers.
Hint: Consider the geometry of the complex and the nature of the ligands involved.
Step 4: Conclusion
After analyzing all the options, the complex that exists as a pair of enantiomers is Cis (CoCl2(en)) and Octahedral (Co(en)3)3+. However, since the question asks for a single complex, the best answer is Cis (CoCl2(en)) as it is the most straightforward example of a complex that can form enantiomers.
Final Answer: The complex that exists as a pair of enantiomers is Cis (CoCl2(en)).
Enantiomers are pairs of molecules that are non-superimposable mirror images of each other. This means that if you were to place one molecule over its mirror image, they would not align perfectly.
We need to analyze the given options to see which complex can form enantiomers. The options provided are:
1. Trans (CoCl2(en))
2. Cis (CoCl2(en))
3. Square planar (Pt(PPh3)(Cl)(Br)(CN))
4. Octahedral (Co(en)3)3+
1. Trans (CoCl2(en)): In this complex, the two chloride ligands are positioned opposite each other (180 degrees apart). This arrangement allows for a plane of symmetry, making it optically inactive and therefore not capable of forming enantiomers.
After analyzing all the options, the complex that exists as a pair of enantiomers is Cis (CoCl2(en)) and Octahedral (Co(en)3)3+. However, since the question asks for a single complex, the best answer is Cis (CoCl2(en)) as it is the most straightforward example of a complex that can form enantiomers.
Topper's Solved these Questions
Similar Questions
Knowledge Check
Enantiomers are
Amolecule that have at least one chiral carbonBnon-superimposible molecules that are mirror images of one anotherCnon-superimposible constitutional isomersDnon-superimposible moleculesWhich is not the pair of enantiomers ?
A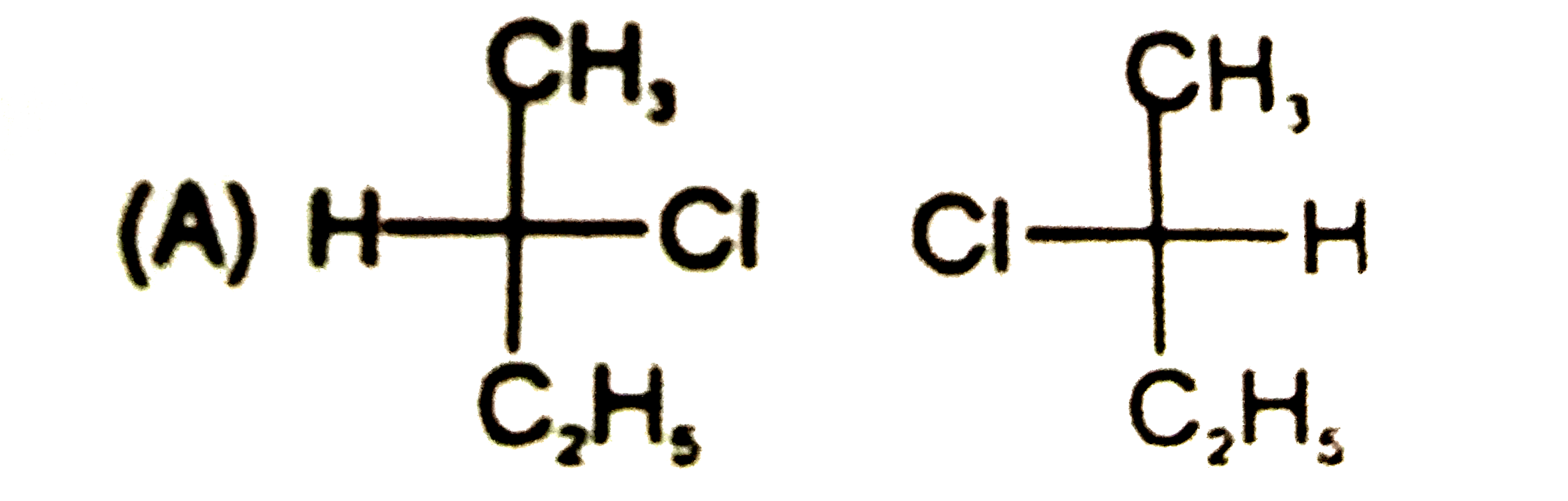 B
B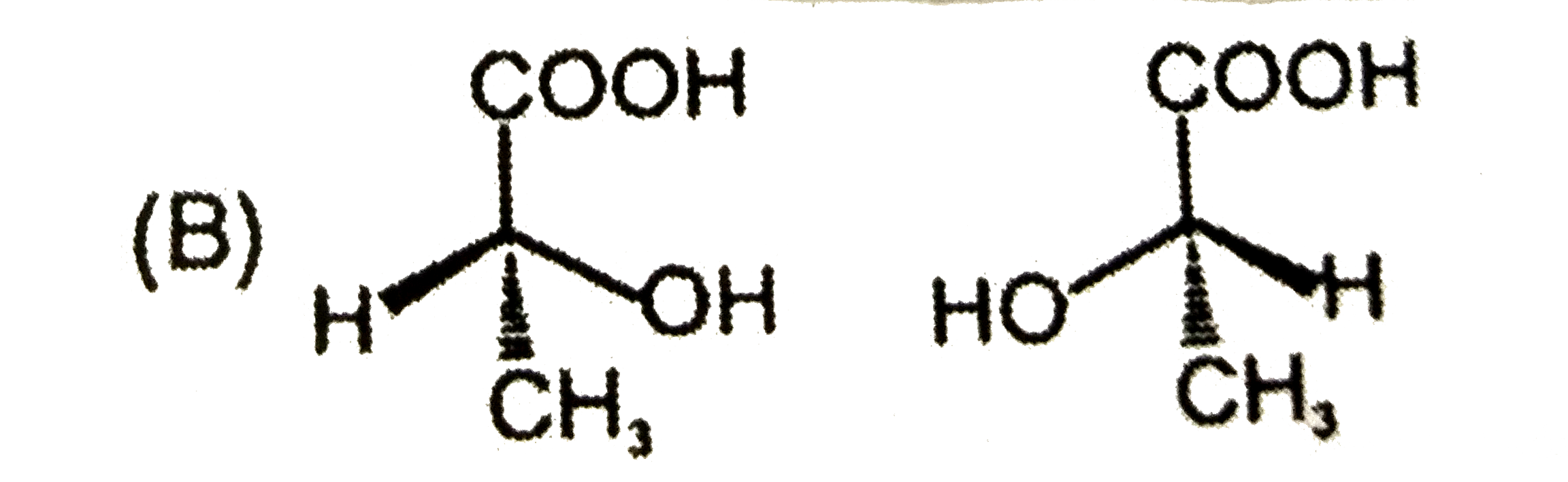 C
C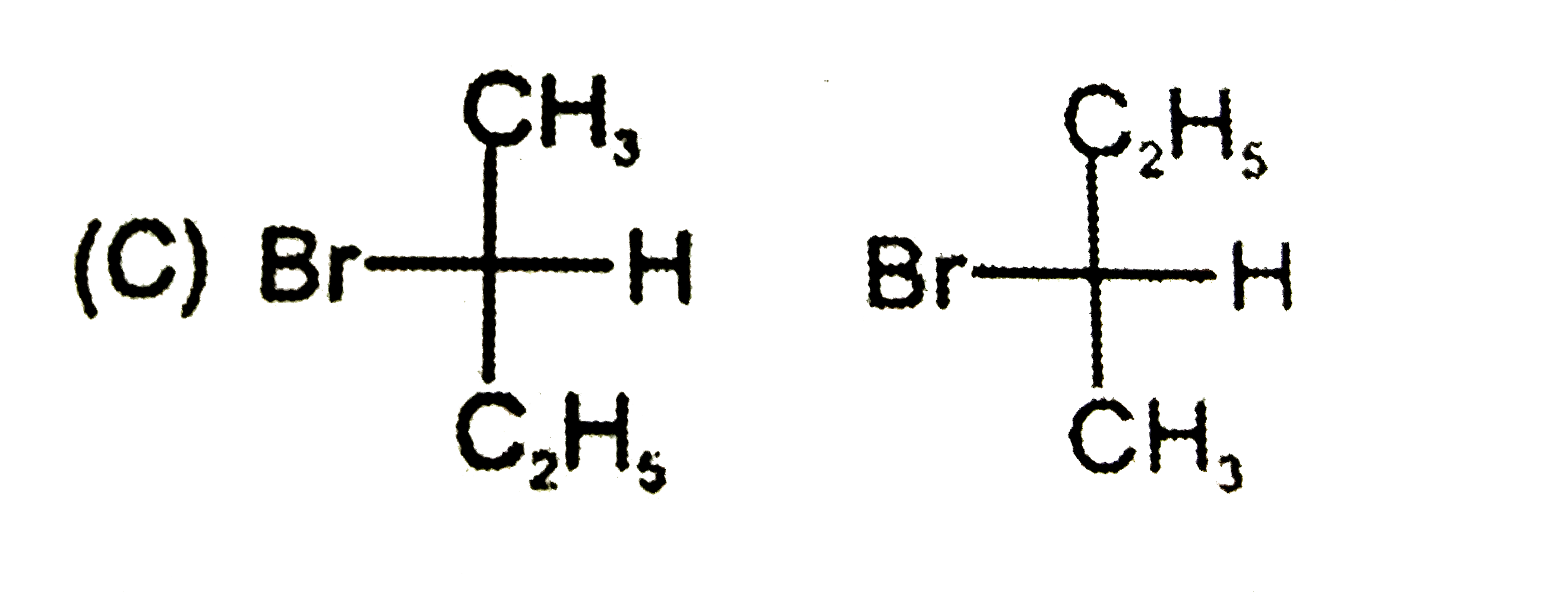 D
D
The two projection formulae that represent a pair of enantiomers are.
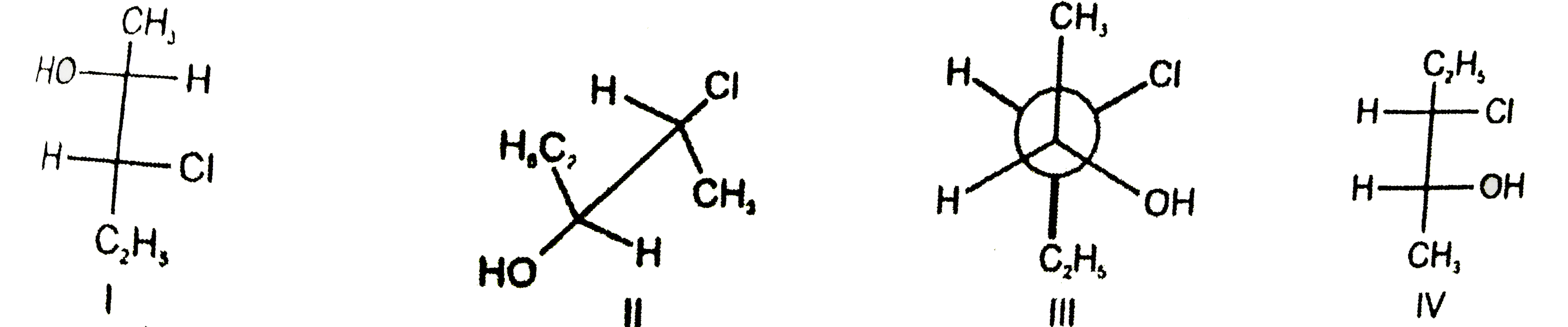 AI and IIBIII and IVCI and IIIDII and IV
AI and IIBIII and IVCI and IIIDII and IV
Enantiomers have
View SolutionWhich of the following compounds can exist both as a cis pair of enantiomers and a trans pair of enantiomers?
View SolutionEnantiomers have:
View SolutionThe following represents a pair of enantiomers:
View SolutionWhich of the following complexes will give a pair of enantiomers ?
View Solution

