Given that standard potential for the following half - cell reaction at 298 K,
Cu+(aq)+e−→Cu(s),E∘=0.52V
Cu2+(aq)+e−→Cu+(aq),E∘=0.16V
Calculate the ΔG∘(kJ) for the eaction, [2Cu+(aq)→Cu(s)+Cu2+]
−34.740
−65.720
−69.720
−131.440
The correct Answer is:A
To solve the problem, we need to calculate the standard Gibbs free energy change (ΔG°) for the reaction:
2Cu+(aq)→Cu(s)+Cu2+(aq)
Step 1: Identify the Half-Reactions
We have two half-reactions with their standard potentials:
1. Reduction of Cu⁺ to Cu:
Cu+(aq)+e−→Cu(s),E∘=0.52V
2. Reduction of Cu²⁺ to Cu⁺:
Cu2+(aq)+2e−→Cu+(aq),E∘=0.16V
Step 2: Reverse the Second Half-Reaction
To obtain the desired reaction, we need to reverse the second half-reaction:
Cu+(aq)→Cu2+(aq)+e−,E∘=−0.16V
Step 3: Combine the Half-Reactions
Now we can add the two half-reactions together:
1. From the first half-reaction:
Cu+(aq)+e−→Cu(s)
2. From the reversed second half-reaction:
Cu+(aq)→Cu2+(aq)+e−
Adding these gives:
2Cu+(aq)→Cu(s)+Cu2+(aq)
Step 4: Calculate the Standard Cell Potential (E°)
The standard cell potential for the overall reaction is calculated as follows:
E∘cell=E∘reduction+E∘oxidation
E∘cell=0.52V+(−0.16V)
E∘cell=0.52V−0.16V=0.36V
Step 5: Calculate ΔG°
Using the formula:
ΔG∘=−nFE∘cell
Where:
- n=2 (since 2 moles of electrons are transferred in the overall reaction)
- F=96500C/mol (Faraday's constant)
- E∘cell=0.36V
Calculating ΔG°:
ΔG∘=−2×96500C/mol×0.36V
ΔG∘=−2×96500×0.36
ΔG∘=−69360J/mol
Step 6: Convert to kJ
To convert from joules to kilojoules:
ΔG∘=−69.36kJ/mol
Final Answer
Thus, the final answer for ΔG° for the reaction is:
ΔG∘≈−69.36kJ
We have two half-reactions with their standard potentials:
Cu+(aq)+e−→Cu(s),E∘=0.52V
Cu2+(aq)+2e−→Cu+(aq),E∘=0.16V
To obtain the desired reaction, we need to reverse the second half-reaction:
Now we can add the two half-reactions together:
Cu+(aq)+e−→Cu(s)
Cu+(aq)→Cu2+(aq)+e−
2Cu+(aq)→Cu(s)+Cu2+(aq)
The standard cell potential for the overall reaction is calculated as follows:
E∘cell=E∘reduction+E∘oxidation
E∘cell=0.52V+(−0.16V)
E∘cell=0.52V−0.16V=0.36V
Using the formula:
ΔG∘=−nFE∘cell
Where:
- n=2 (since 2 moles of electrons are transferred in the overall reaction)
- F=96500C/mol (Faraday's constant)
- E∘cell=0.36V
ΔG∘=−2×96500C/mol×0.36V
ΔG∘=−2×96500×0.36
ΔG∘=−69360J/mol
To convert from joules to kilojoules:
ΔG∘=−69.36kJ/mol
Thus, the final answer for ΔG° for the reaction is:
ΔG∘≈−69.36kJ
Topper's Solved these Questions
Similar Questions
Knowledge Check
If for the half cell reaction E∘ value are given
Cu2++e−→Cu+,E∘=0.15V
Cu2++2e−→Cu+,E∘=0.34V
calculate E∘ of the half cell reaction
Cu++e−→CuA+0.53VB−0.53VC−0.80VD−0.28VAg+(aq)+e−→Ag(s)E∘=0.80V
Cu2+(aq)+2e−→Cu(s)E∘=0.34V

What is the value for ΔG∘ when [Ag+]=[Cu+]=1.0M?A−44.4kJB−88.8kJC−242kJD−374kJGiven:
(i) Cu2++2e−→Cu,E∘=0.337V
(ii) Cu2++e−→Cu+,E∘=0.153V
Electrode potential, E∘ for the reaction, Cu++e−→Cu, will beA0.90VB0.30VC0.38VD0.52V
Calculate the standard free enegry change for the reaction:
Zn+Cu2+(aq)→Cu+Zn2+(aq),EΘ=1.20V
View SolutionGiven:
(i) Cu2++2e−→Cu,E∘=0.337V
(ii) Cu2++e−→Cu+,E∘=0.153V
Electrode potential, E∘ for the reaction, Cu++e−→Cu, will be
View SolutionRh03+(aq)+3e−→Rh(s)E∘=0.80V
Cu+(aq)+e−→Cu(s)E∘=0.52V

What is the voltage of this cell if the concentrations of Cu+ and Rh3+ are each 1 M?
View SolutionThe standard potential E∘ for the half reactions are as :
Zn→Zn2++2e−,E∘=0.76V
Cu→Cu2++2e−,E∘=−0.34V
The standard cell voltage for the cell reaction is ?
Zn+Cu2→Zn2++Cu
View SolutionAg+(aq)+e−→Ag(s)E∘=0.80V
Cu2+(aq)+2e−→Cu(s)E∘=0.34V
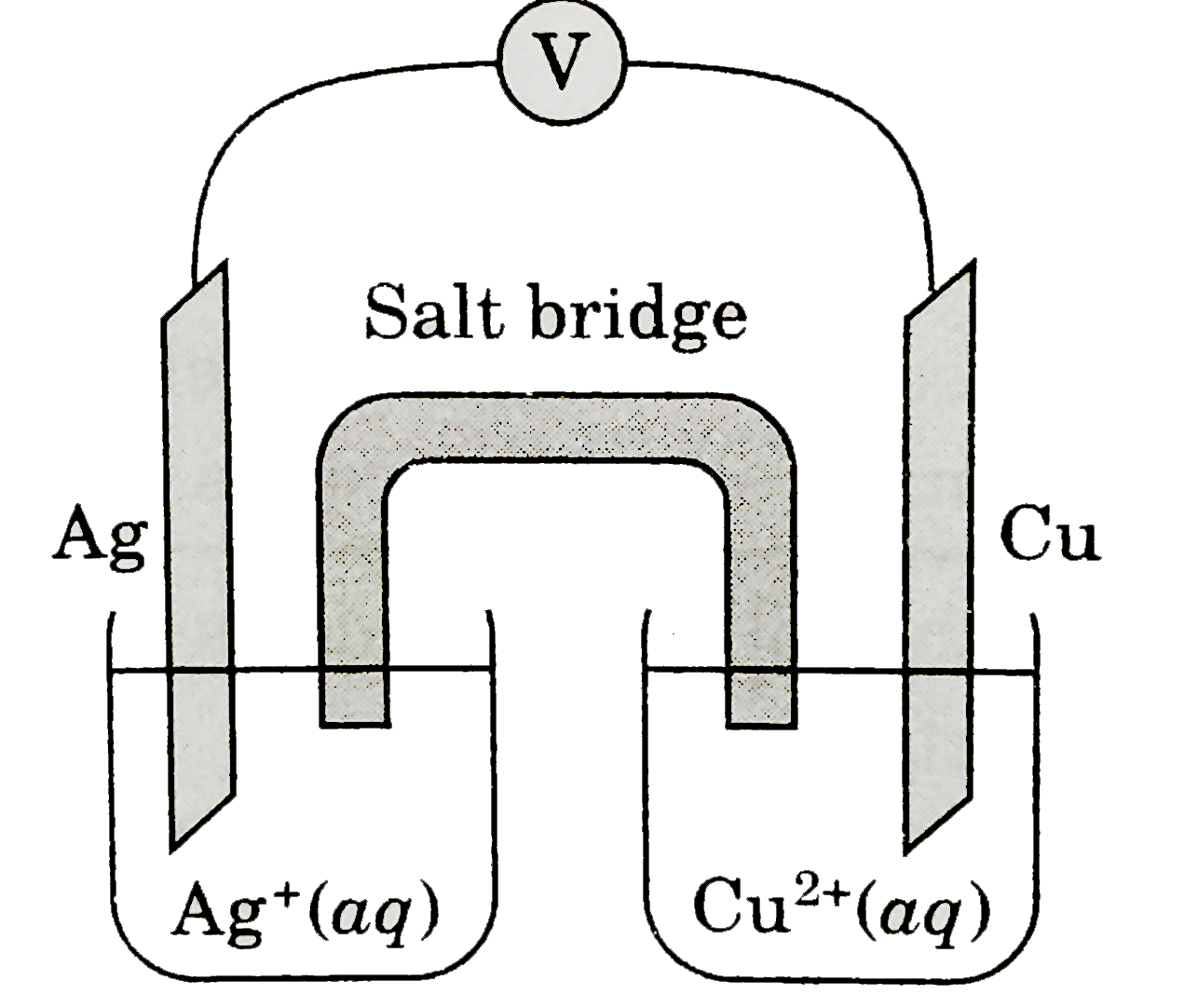
Which expression gives the voltage for this cell if [Cu2+]=1.00M and [Ag+]=0.010M?
View Solution
