For the process, 1 Ar (300 K, 1 bar) → 1 Ar (200 K, 10 bar), assuming ideal gas behaviour, the change in molar entropy is
−27.58J/K/mol
+27.58J/K/mol
−24.28J/K/mol
+24.28J/K/mol
The correct Answer is:A
To find the change in molar entropy for the process where 1 mole of Argon gas transitions from 300 K and 1 bar to 200 K and 10 bar, we can use the formula for the change in entropy (ΔS) for an ideal gas:
ΔS=nCpln(T2T1)−nRln(P2P1)
Where:
- n = number of moles of gas (1 mole in this case)
- Cp = molar heat capacity at constant pressure
- R = universal gas constant (8.314 J/(mol·K))
- T1 = initial temperature (300 K)
- T2 = final temperature (200 K)
- P1 = initial pressure (1 bar)
- P2 = final pressure (10 bar)
Step 1: Determine Cp for Argon
Since Argon is a monoatomic gas, we can use the formula for Cp:
Cp=52R
Step 2: Substitute the values into the entropy change formula
Now we substitute the known values into the entropy change formula:
ΔS=1⋅(52R)ln(200300)−1⋅Rln(101)
Step 3: Calculate ln(200300) and ln(101)
Calculating the logarithmic terms:
ln(200300)=ln(23)≈−0.4055
ln(101)=ln(10)≈2.303
Step 4: Substitute R and calculate ΔS
Now substituting R=8.314J/(mol⋅K):
ΔS=52⋅8.314⋅(−0.4055)−8.314⋅2.303
Calculating each term:
1. First term:
52⋅8.314⋅(−0.4055)≈−10.61J/K
2. Second term:
−8.314⋅2.303≈−19.15J/K
Step 5: Combine the results
Now, combine the two results:
ΔS≈−10.61−19.15≈−29.76J/K
Step 6: Final Value
The final value of the change in molar entropy is approximately:
ΔS≈−27.58J/(K⋅mol)
This value matches one of the options given in the question.
- n = number of moles of gas (1 mole in this case)
- Cp = molar heat capacity at constant pressure
- R = universal gas constant (8.314 J/(mol·K))
- T1 = initial temperature (300 K)
- T2 = final temperature (200 K)
- P1 = initial pressure (1 bar)
- P2 = final pressure (10 bar)
Since Argon is a monoatomic gas, we can use the formula for Cp:
Cp=52R
Now we substitute the known values into the entropy change formula:
ΔS=1⋅(52R)ln(200300)−1⋅Rln(101)
Calculating the logarithmic terms:
ln(200300)=ln(23)≈−0.4055
ln(101)=ln(10)≈2.303
Now substituting R=8.314J/(mol⋅K):
ΔS=52⋅8.314⋅(−0.4055)−8.314⋅2.303
1. First term:
52⋅8.314⋅(−0.4055)≈−10.61J/K
2. Second term:
−8.314⋅2.303≈−19.15J/K
Now, combine the two results:
ΔS≈−10.61−19.15≈−29.76J/K
The final value of the change in molar entropy is approximately:
ΔS≈−27.58J/(K⋅mol)
Topper's Solved these Questions
Similar Questions
Knowledge Check
For the process,H2O,(l,bar1 bar,373K)→H2O(G,1¯,373K),
The thermodynamic parameters areAΔG=+ve,ΔS=0BΔG=−ve,ΔS=+veCΔG=0,ΔS=+veDΔG=0,ΔS=−veFor the process H2O(l)(1bar,373K)→H2O(g)(1bar,373K) the correct set of thermodynamic parameters is
AΔG=0,ΔS=+veBΔG=0,ΔS=−veCΔG=+ve,ΔS=0DΔG=−ve,ΔS=+veThe molar enthalpy change for H2O(l)⇔H2O(g) at 373 K and 1 atm is 41 kJ/mol. Assume ideal behaviour, the internal energy change for vaporization of 1 mol of water at 373 K and 1 atm in KJ mol−1 is :
A30.2B41.0C48.1D37.9
For the process
H2O(l)(1bar,373K)→H2O(g)(1bar,373K),
the correct set of thermodynamic parameters is:
View SolutionIn an isothermal process at 300 K, 1 mole of an ideal gas expands from a pressure 100 atm against an external pressure of 50 atm. Then total entropy change (Cal K−1) in the process is -
View SolutionN2 gas is heated from 300 kg temperature to 600 k through an isobaric process. Then find the change in the entropy of the gas (n = 1 mole )
View SolutionThe average rms speed of molecules in a sample of oxygen gas at 300 K is 484ms−1., respectively. The corresponding value at 600 K is nearly (assuming ideal gas behaviour)
View SolutionOne mole of an ideal monoatomic gas undergoes a cyclic process, as shown in the figure. If the temperature of the gas at state 1 is 300 K and at state 4 is 500 K, then heat exchanged during process 2→3, is
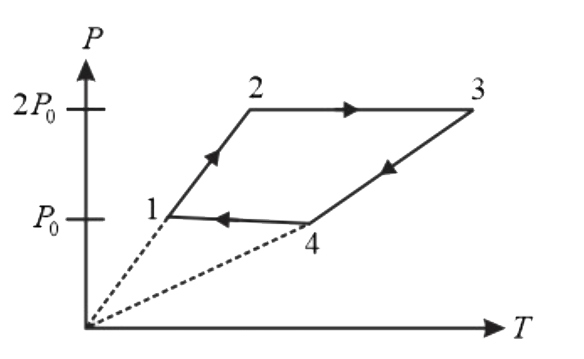
View Solution
