A boy throws a stone with a speed of V0=10 m/sec at an angle of θ0=30∘ to the horizontal Find the position of the stone wrt the point of projection just after a time t = 1/2 sec.
The correct Answer is:5√32,54
To solve the problem of finding the position of the stone with respect to the point of projection just after a time t=12 seconds, we can break it down into the following steps:
Step 1: Identify the initial conditions
- Initial speed V0=10m/s
- Angle of projection θ0=30∘
Step 2: Calculate the initial velocity components
Using trigonometric functions, we can find the horizontal and vertical components of the initial velocity:
- Horizontal component V0x=V0cos(θ0)=10cos(30∘)
- Vertical component V0y=V0sin(θ0)=10sin(30∘)
Calculating these:
- cos(30∘)=√32
- sin(30∘)=12
Thus:
- V0x=10×√32=5√3m/s
- V0y=10×12=5m/s
Step 3: Calculate the position after t=12 seconds
The position can be calculated using the equations of motion. The horizontal and vertical displacements can be calculated separately.
Horizontal displacement x:
x=V0x⋅t
Substituting the values:
x=5√3⋅12=5√32m
Vertical displacement y:
The vertical displacement is affected by gravity. The equation for vertical displacement is:
y=V0y⋅t−12gt2
Where g≈9.81m/s2. Substituting the values:
y=5⋅12−12⋅9.81⋅(12)2
Calculating:
y=2.5−12⋅9.81⋅14=2.5−9.818≈2.5−1.22625≈1.27375m
Step 4: Final position of the stone
The position of the stone with respect to the point of projection after t=12 seconds is:
Position=(5√32,1.27375)m
Summary of the solution:
- Horizontal displacement x≈4.33m (since √3≈1.732)
- Vertical displacement y≈1.27m
- Initial speed V0=10m/s
- Angle of projection θ0=30∘
Using trigonometric functions, we can find the horizontal and vertical components of the initial velocity:
- Horizontal component V0x=V0cos(θ0)=10cos(30∘)
- Vertical component V0y=V0sin(θ0)=10sin(30∘)
- cos(30∘)=√32
- sin(30∘)=12
- V0x=10×√32=5√3m/s
- V0y=10×12=5m/s
The position can be calculated using the equations of motion. The horizontal and vertical displacements can be calculated separately.
x=V0x⋅t
Substituting the values:
x=5√3⋅12=5√32m
The vertical displacement is affected by gravity. The equation for vertical displacement is:
y=V0y⋅t−12gt2
Where g≈9.81m/s2. Substituting the values:
y=5⋅12−12⋅9.81⋅(12)2
Calculating:
y=2.5−12⋅9.81⋅14=2.5−9.818≈2.5−1.22625≈1.27375m
The position of the stone with respect to the point of projection after t=12 seconds is:
Position=(5√32,1.27375)m
- Horizontal displacement x≈4.33m (since √3≈1.732)
- Vertical displacement y≈1.27m
Topper's Solved these Questions
- KINEMATICSBOOK - FIITJEECHAPTER - KINEMATICSEXERCISE - ASSIGNMENT PROBLEMS (SUBJECTIVE) LEVEL-II & III
15 Videos
- KINEMATICSBOOK - FIITJEECHAPTER - KINEMATICSEXERCISE - ASSIGNMENT PROBLEMS (OBJECTIVE) LEVEL-I
45 Videos
- KINEMATICSBOOK - FIITJEECHAPTER - KINEMATICSEXERCISE - ASSIGNMENT PROBLEMS (SUBJECTIVE) LEVEL-I (True/False)
2 Videos
- HEAT AND TEMPERATUREBOOK - FIITJEECHAPTER - HEAT AND TEMPERATUREEXERCISE - NUMERICAL BASES QUESTIONS
1 Videos
- LAWS OF MOTIONBOOK - FIITJEECHAPTER - LAWS OF MOTIONEXERCISE - COMPREHENSION-III
2 Videos
Similar Questions
A particle of mass m is projected with a speed v0 at an angle of projection θ with horizontal. Find the torque of the weight of the particle about the point of projection after time v0sinθg
View SolutionA particle of mass m is projected with a speed u at an angle θ with the horizontal. Find angular momentum of particle after time t about point of projection.
View Solution
Knowledge Check
A stone is projected with speed of 50ms−1 at an angle of 60∘ with the horizontal. The speed of the stone at highest point of trajectory is
A75ms−1B25ms−1C50ms−1Dcannot findA particle is projected with a velocity of 39.2m/sec at an angle of 30∘ to the horizontal. It will move at right angles to the direction of projection after the time
A8 secB5 secC6 secD10 sec
A particle of mass m is projected at t=0 from the point P on the ground with speed v0 at an angle of θ to the horizontal. Find the magnitude and direction of the angular momentum of the particle at time t=v0sinθ2g.
View SolutionA particle of mass m is thrown with speed v0 at angle 30∘ with horizontal. Find the angular momentum about the point of projection when the particle is at the highest point of its trajectory.
View SolutionA particle is projected at time t=0 from a point P on the ground with a speed v0, at an angle of 45∘ to the horizontal. Find the magnitude and direction of the angular momentum of the particle about P at tiem t=v0/g
View SolutionA stone is thrown from the top of a tower of height 50 m with a velocity of 30 m per second at an angle of 30∘ above the horizontal. Find (a) the time during which the stone will be in air, (b) the distance from the tower base to where the stone will hit the ground, (c) the speed with which the stone will hit the ground, (d) the angle formed by the trajectory of the stone with the horizontal at the point of hit.
View SolutionA particle is projected with a speed of 10m/s at an angle 37∘ from horizontal, anglular speed to particle with respect to point of projection at t=0.5sec. Is (16X61) rad/sec then calculate X :
View SolutionA boy standing on a cliff 50 m high throws a ball with speed 40m/s directly aiming towards a man standing on ground at B. At the same time the man at B throws a stone with a speed of 10m/s directly aiming towards the boy.
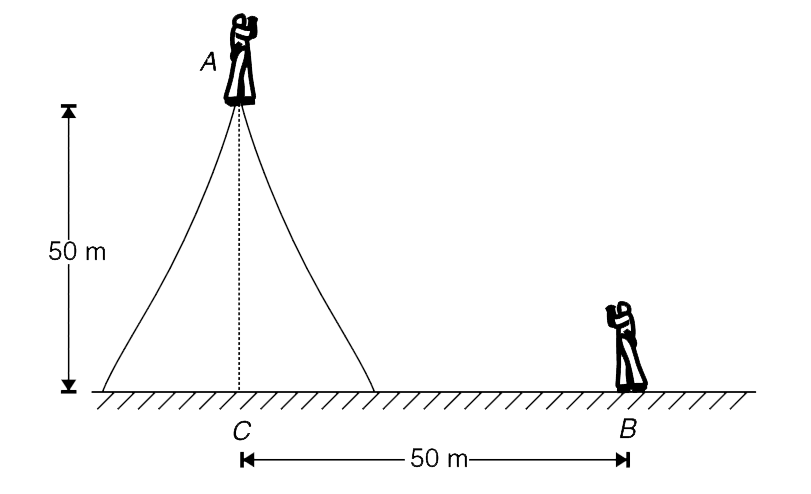
(a) Will the ball and the stone collide? If yes, at what time after projection?
(b) At what height above the ground the two objects collide?
(c) Draw the path of ball in the reference frame of the stone.
View Solution
