A particle starts moving due east with a velocity V1=5 m/sec. for 10 sec, turns to north and moves with a velocity V2=10 m/sec. for 5 sec. Find the average velocity of the particle during 15 sec. from starting.
To find the average velocity of the particle during the 15 seconds of motion, we can follow these steps:
Step 1: Calculate the distance traveled in the east direction
The particle moves due east with a velocity V1=5 m/s for a time of t1=10 seconds.
Using the formula for distance:
D1=V1×t1
Substituting the values:
D1=5m/s×10s=50m
Step 2: Calculate the distance traveled in the north direction
Next, the particle turns north and moves with a velocity V2=10 m/s for a time of t2=5 seconds.
Using the same formula for distance:
D2=V2×t2
Substituting the values:
D2=10m/s×5s=50m
Step 3: Determine the total displacement
The total displacement can be found using the Pythagorean theorem since the two distances are perpendicular to each other (east and north).
Displacement=√D21+D22
Substituting the values:
Displacement=√(50m)2+(50m)2=√2500+2500=√5000=50√2m
Step 4: Calculate the total time taken
The total time taken for the motion is:
Total time=t1+t2=10s+5s=15s
Step 5: Calculate the average velocity
The average velocity is given by the formula:
Average velocity=Total displacementTotal time
Substituting the values:
Average velocity=50√2m15s=10√23m/s
Step 6: Approximate the average velocity
To approximate √2≈1.41:
Average velocity≈10×1.413≈14.13≈4.7m/s
Conclusion
Thus, the average velocity of the particle during the 15 seconds is approximately 4.7m/s in the direction of North-East.
---
The particle moves due east with a velocity V1=5 m/s for a time of t1=10 seconds.
D1=V1×t1
Substituting the values:
D1=5m/s×10s=50m
Next, the particle turns north and moves with a velocity V2=10 m/s for a time of t2=5 seconds.
D2=V2×t2
Substituting the values:
D2=10m/s×5s=50m
The total displacement can be found using the Pythagorean theorem since the two distances are perpendicular to each other (east and north).
Substituting the values:
Displacement=√(50m)2+(50m)2=√2500+2500=√5000=50√2m
The total time taken for the motion is:
Total time=t1+t2=10s+5s=15s
The average velocity is given by the formula:
Average velocity=Total displacementTotal time
Substituting the values:
Average velocity=50√2m15s=10√23m/s
To approximate √2≈1.41:
Average velocity≈10×1.413≈14.13≈4.7m/s
Thus, the average velocity of the particle during the 15 seconds is approximately 4.7m/s in the direction of North-East.
Topper's Solved these Questions
- KINEMATICSBOOK - FIITJEECHAPTER - KINEMATICSEXERCISE - ASSIGNMENT PROBLEMS (SUBJECTIVE) LEVEL-II & III
15 Videos
- KINEMATICSBOOK - FIITJEECHAPTER - KINEMATICSEXERCISE - ASSIGNMENT PROBLEMS (OBJECTIVE) LEVEL-I
45 Videos
- KINEMATICSBOOK - FIITJEECHAPTER - KINEMATICSEXERCISE - ASSIGNMENT PROBLEMS (SUBJECTIVE) LEVEL-I (True/False)
2 Videos
- HEAT AND TEMPERATUREBOOK - FIITJEECHAPTER - HEAT AND TEMPERATUREEXERCISE - NUMERICAL BASES QUESTIONS
1 Videos
- LAWS OF MOTIONBOOK - FIITJEECHAPTER - LAWS OF MOTIONEXERCISE - COMPREHENSION-III
2 Videos
Similar Questions
Afrala moves due east with a velocity 20 m/s and a car moves due north with a velocity v2=15m/sec. Find the velocity of the car as observed by a passenger sitting in the train
View SolutionA particle moves in straight line in same direction for 20 seconds with velocity 3m/s and the moves with velocity 4m/s for another 20 sec and finally moves with velocity 5m/s for next 20 seconds. What is the average velocity of the particle?
View Solution
Knowledge Check
A particle is moving eastwards with a velocity 15ms−1.Suddenly it moves towards north and moves with the same speed in time 10sec.The average acceleration during this time is
A3/√2NEB3/√2NEC3/√2NWD3/√2NWA particle starts moving with constant, velocity v=ms, from position x=5m The position time graph will be
A B
B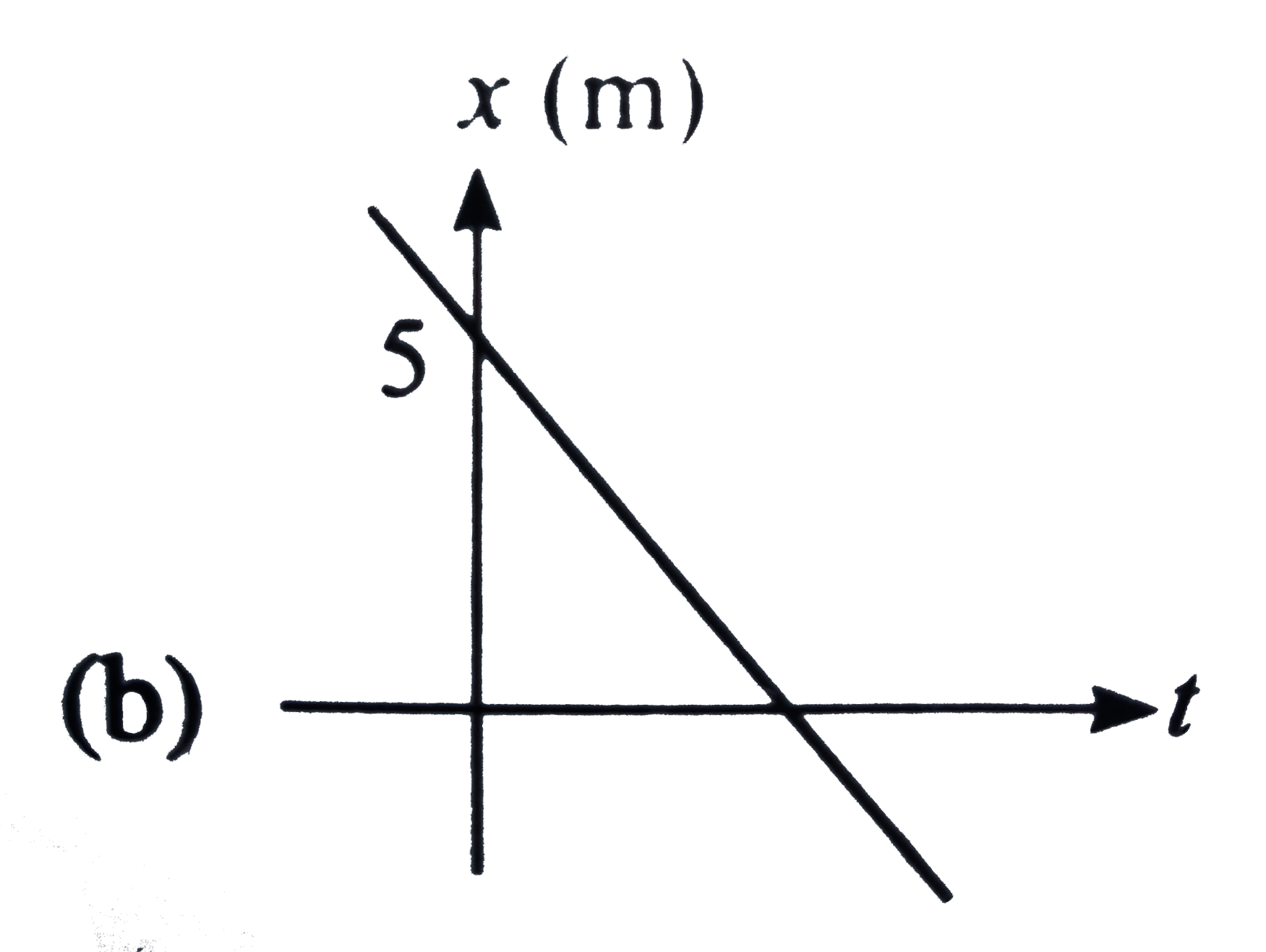 C
C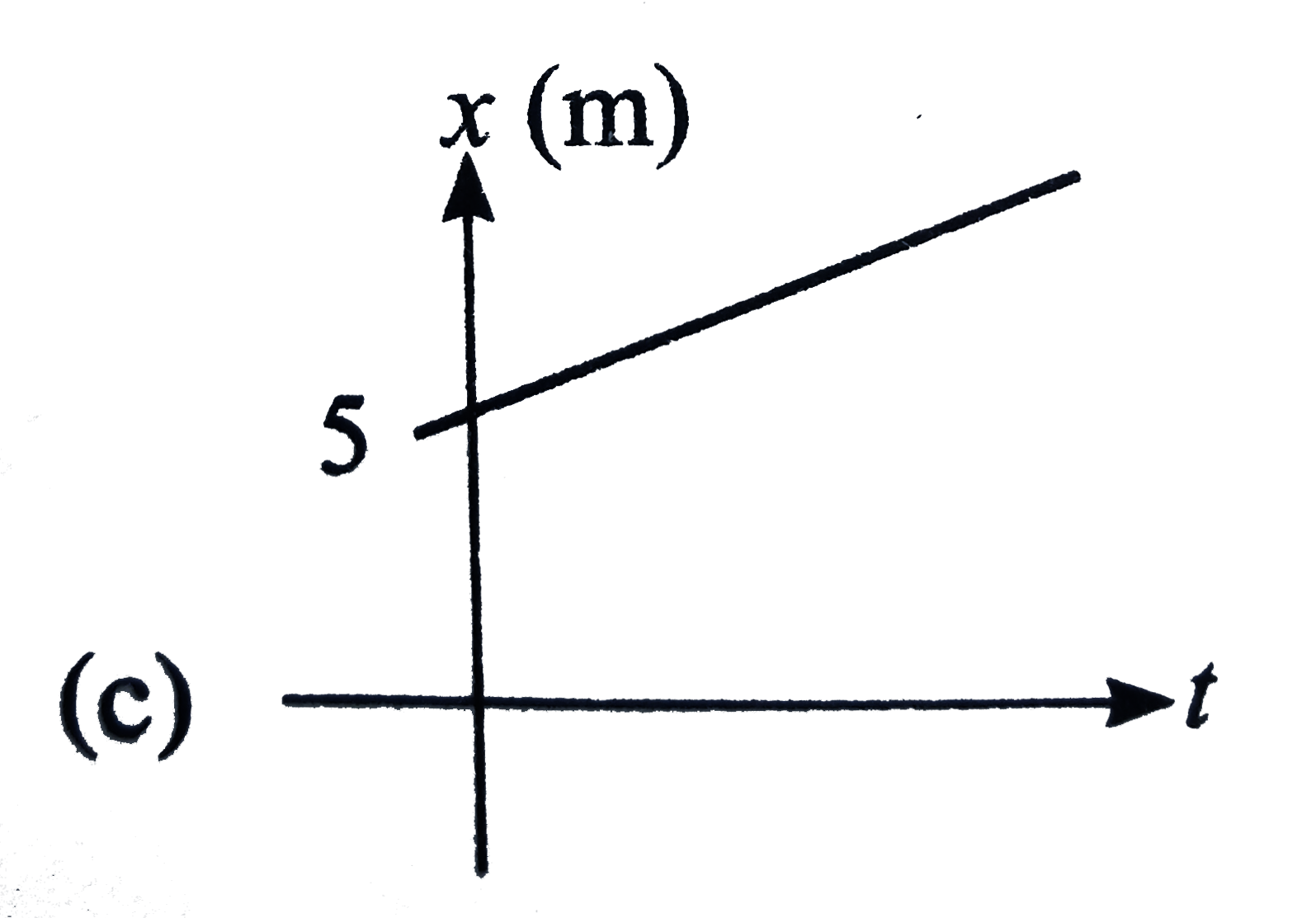 D
D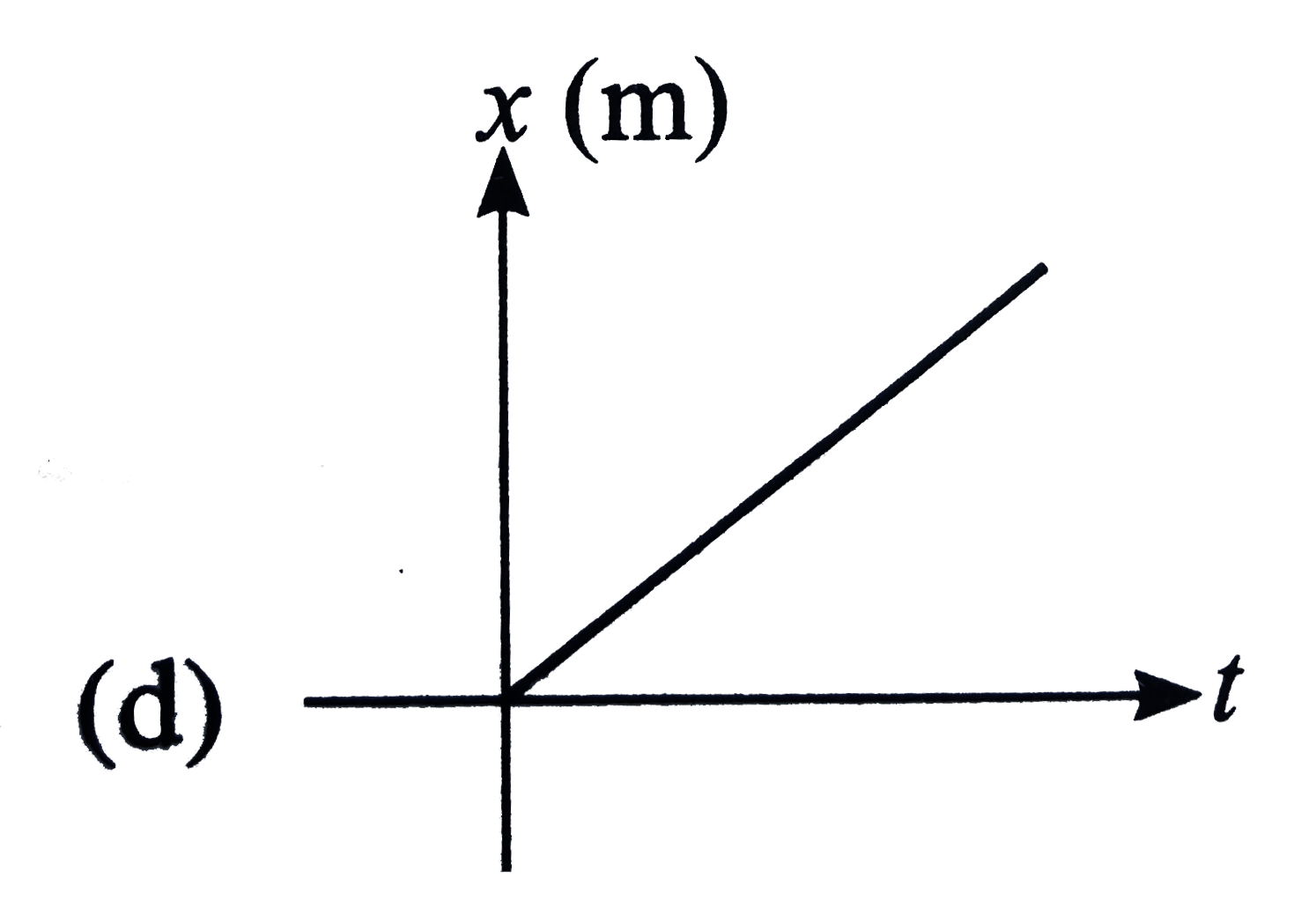
A particle is moving with velocity 5 m/s towards cast and its velocity changes to 5 m/s north in 10 s, find the acceleration .
A√2 N-WB1√2 N-WC1√2 N-ED√2N−E
A particle moves in east direction with 15m/sec for 2 sec then moves in northward with 5 m/s for 8 sec. A average speed of the particle is :-
View SolutionX is moving with velocity 2m/sec. due east and Y is moving with velocity 4m/sec due west Find (1) The velocity of Y with respect to X, (2) Velocity of X with respect to Y
View SolutionA particle is moving eastwards with a velocity of 5m/s. In 10s the velocity changes to 5m/s nothwards. The average acceleration in this time is
View SolutionA particle is moving eastwards with velocity of 5m/s. In 10sec the velocity changes to 5m/s northwards. The average acceleration in this time is.
View SolutionA ball of mass 0.2 kg moves with a velocity of 20m/sec and it stops in 0.1 sec , then the force on the ball is
View Solution
