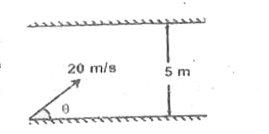
A projectile is projected with a speed = 20 m/s from the floor of a 5 m high room as shown. Find the maximum horizontal range of the projectile and the corresponding angle of projection θ.
The correct Answer is:20√3m and theta=30^(@)~
Step by step video, text & image solution for A projectile is projected with a speed = 20 m/s from the floor of a 5 m high room as shown. Find the maximum horizontal range of the projectile and the corresponding angle of projection theta. by Physics experts to help you in doubts & scoring excellent marks in Class 12 exams.
Topper's Solved these Questions
- BOOK - FIITJEECHAPTER - KINEMATICSEXERCISE - ASSIGNMENT PROBLEMS (OBJECTIVE) LEVEL-I45videos
KINEMATICS
- BOOK - FIITJEECHAPTER - KINEMATICSEXERCISE - ASSIGNMENT PROBLEMS (OBJECTIVE) LEVEL-I (ASSERTION REASONING TYPE)2videos
KINEMATICS
- BOOK - FIITJEECHAPTER - KINEMATICSEXERCISE - ASSIGNMENT PROBLEMS (SUBJECTIVE) LEVEL-I (Numerical)8videos
KINEMATICS
- BOOK - FIITJEECHAPTER - HEAT AND TEMPERATUREEXERCISE - NUMERICAL BASES QUESTIONS1videos
HEAT AND TEMPERATURE
- BOOK - FIITJEECHAPTER - LAWS OF MOTIONEXERCISE - COMPREHENSION-III2videos
LAWS OF MOTION
Similar Questions
An object is projected with speed u and range of the projectile is found to be double of the maximum height attained by it . Range of the projectile is .
View SolutionAn object is projected with speed u and range of the projectile is found to be double of the maximum height attained by it . Range of the projectile is .
View Solution
Knowledge Check
- Question 1 - Select One
The horizontal range of a projectile is times of its maximum height. Its angle of projection will be :-
A45∘B60∘C90∘D30∘ - Question 2 - Select One
The horizontal range and the maximum height of a projectile are equal. The angle of projection of the projectile is
Aθ=tan−1(14)Bθ=tan−1(4)Cθ=tan−1(2)Dθ=45∘ - Question 3 - Select One
The horizontal range of a projectile is 4√3 times its maximum height. The angle of projection is
A30∘B45∘C60∘DNone
If R and H represent horizontal range and maximum height of the projectile, then the angle of projection with the horizontal is
View SolutionFour projectiles are projected with the same speed at angles 20∘,35∘,60∘and75∘
with the horizontal. The range will be the maximum for the projectile whose angle of projection isView SolutionThe horizontal range of a projectile is 2√3 times its maximum height. Find the angle of projection.
View SolutionThe horizontal range of a projectile is 4√3 times its maximum height. Its angle of projection will be
View SolutionThe horizontal range is four times the maximum height attained by a projectile. The angle of projection is
View Solution

