A particle (P) is projected at an angle of 82∘ from horizontal with a velocity 6√2m/s from the bottom of an inclined plane, having angle of inclination 37∘ At the same instant, another particle: Q is released from a heighth on a smooth incline plane. If after some time both particles collide, then find the
(a) value of time after which they collide,
(b) the height h

The correct Answer is:(a) 1.5 sec (b) 5.4 m
Step by step video, text & image solution for A particle (P) is projected at an angle of 82^(@) from horizontal with a velocity 6sqrt2 m//s from the bottom of an inclined plane, having angle of inclination 37^(@) At the same instant, another particle: Q is released from a heighth on a smooth incline plane. If after some time both particles collide, then find the (a) value of time after which they collide, (b) the height h by Physics experts to help you in doubts & scoring excellent marks in Class 12 exams.
Topper's Solved these Questions
- BOOK - FIITJEECHAPTER - KINEMATICSEXERCISE - ASSIGNMENT PROBLEMS (OBJECTIVE) LEVEL-I45videos
KINEMATICS
- BOOK - FIITJEECHAPTER - KINEMATICSEXERCISE - ASSIGNMENT PROBLEMS (OBJECTIVE) LEVEL-I (ASSERTION REASONING TYPE)2videos
KINEMATICS
- BOOK - FIITJEECHAPTER - KINEMATICSEXERCISE - ASSIGNMENT PROBLEMS (SUBJECTIVE) LEVEL-I (Numerical)8videos
KINEMATICS
- BOOK - FIITJEECHAPTER - HEAT AND TEMPERATUREEXERCISE - NUMERICAL BASES QUESTIONS1videos
HEAT AND TEMPERATURE
- BOOK - FIITJEECHAPTER - LAWS OF MOTIONEXERCISE - COMPREHENSION-III2videos
LAWS OF MOTION
Similar Questions
A particle is projected from the bottom of an inclined plane of inclination 30∘. At what angle α(from the horizontal) should the particle be projected to get the maximum range on the inclined plane.
View SolutionA block is released from top of a smooth inclined plane.It reaches the bottom of the plane in 6 sec.The time taken by the body to cover the first half of the inclined plane is:
View Solution
Knowledge Check
- Question 1 - Select One
A particle is projected with a certain velocity at an angle α above the horizontal from the foot of an inclined plane of inclination 30∘. If the particle strikes the plane normally then α is equal to
A30∘+tan−1(√32)B45∘C60∘D30∘+tan−1(2√3) - Question 2 - Select One
A particle is projected with a certain velocity at an angle ∝ above the horizontal from the foot of an inclined plane of inclination 30∘. If the particle strikes the plane normally, then ∝ is equal to.
A30∘+tan−1(√32)B45∘C60∘D30∘+tan−1(2√3) - Question 3 - Select One
A particle is projected with a velocity u from the foot of an inclined plane whose inclination to the horizon is β. It strikes. the plane at right angles if
Atan(α−β)=cotβB2tan(α−β)=cotβC2cot(α−β)=cotβDNone of these
A particle is projected at an angle α with the horizontal from the foot of an inclined plane making an angle β with horizontal . Which of the following expressions holds good if the particle strikes the inclined plane normally?
View SolutionA particle is projected horizontally with a speed V=5m/s from the top of a plane inclined at an angle θ=37∘ to the horizontal (g=10m/s2)

What is the velocity of the particle just before it hits the plane?View SolutionA particle is projected horizontally with a speed V=5m/s from the top of a plane inclined at an angle θ=37∘ to the horizontal (g=10m/s2)

How far from the point of projection will the particle strike the plane?View SolutionA particle is projected horizontally with a speed V=5m/s from the top of a plane inclined at an angle θ=37∘ to the horizontal (g=10m/s2)
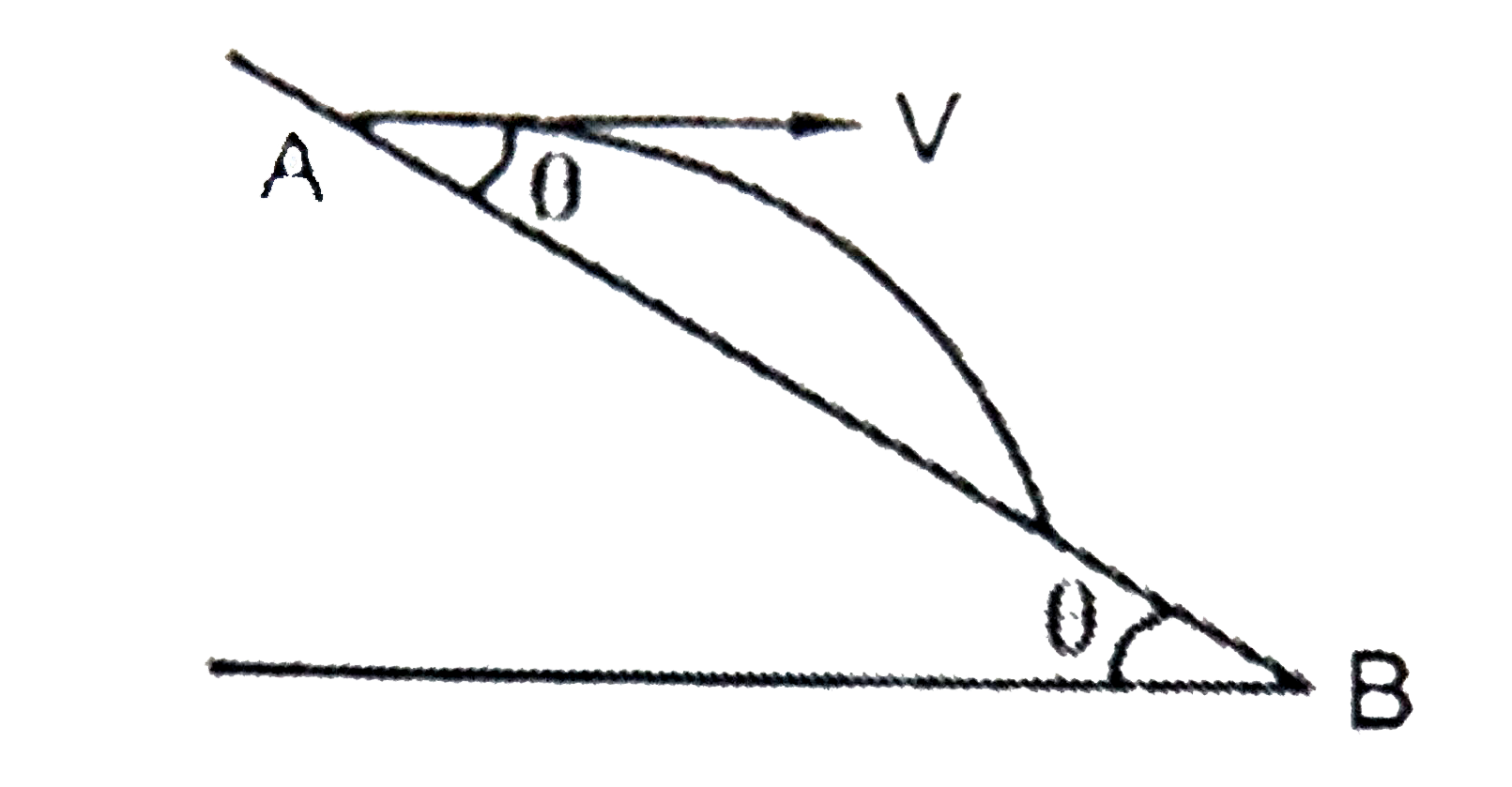
Find the time taken by the particle to hit the plane.View SolutionA particle is projected with a velocity of 20 m/s at an angle of 30∘ to an inclined plane of inclination 30∘ to the horizontal. The particle hits the inclined plane at an angle 30∘, during its journey. The time of flight is -
View Solution

