Two identical particles each of mass m are connected by a light spring of stiffness K. The initial deformation of the spring when the system was at rest, x0. After releasing the system, if one of the particles has a speed v and the deformation of the spring is x, find the speed of the other particle neglecting friction.
The correct Answer is:v∘={km(x20−x2)−v2}1/2
To solve the problem, we will use the principle of conservation of mechanical energy. The initial potential energy stored in the spring when it is deformed by x0 will be equal to the sum of the kinetic energies of the two particles and the potential energy stored in the spring when it is deformed by x.
1. Identify Initial and Final States:
- Initially, the spring is deformed by x0 and both particles are at rest. Thus, the initial kinetic energy is 0.
- After release, one particle has a speed v and the spring is deformed by x.
2. Calculate Initial Energy:
- The initial potential energy Ui stored in the spring when it is deformed by x0 is given by:
Ui=12Kx20
3. Calculate Final Energy:
- The final energy Uf consists of the kinetic energy of both particles and the potential energy stored in the spring when it is deformed by x:
Uf=12mv2+12mv21+12Kx2
- Here, v1 is the speed of the other particle which we need to find.
4. Apply Conservation of Energy:
- According to the conservation of mechanical energy:
Ui=Uf
- Substituting the expressions for initial and final energy:
12Kx20=12mv2+12mv21+12Kx2
5. Simplify the Equation:
- Multiply through by 2 to eliminate the fractions:
Kx20=mv2+mv21+Kx2
- Rearranging gives:
Kx20−Kx2=mv2+mv21
6. Solve for v1:
- Rearranging the equation to isolate v21:
mv21=Kx20−Kx2−mv2
- Dividing by m:
v21=Km(x20−x2)−v2
- Taking the square root to find v1:
v1=√Km(x20−x2)−v2
Final Answer:
The speed of the other particle is:
v1=√Km(x20−x2)−v2
- Initially, the spring is deformed by x0 and both particles are at rest. Thus, the initial kinetic energy is 0.
- After release, one particle has a speed v and the spring is deformed by x.
- The initial potential energy Ui stored in the spring when it is deformed by x0 is given by:
Ui=12Kx20
- The final energy Uf consists of the kinetic energy of both particles and the potential energy stored in the spring when it is deformed by x:
Uf=12mv2+12mv21+12Kx2
- Here, v1 is the speed of the other particle which we need to find.
- According to the conservation of mechanical energy:
Ui=Uf
- Substituting the expressions for initial and final energy:
12Kx20=12mv2+12mv21+12Kx2
- Multiply through by 2 to eliminate the fractions:
Kx20=mv2+mv21+Kx2
- Rearranging gives:
Kx20−Kx2=mv2+mv21
- Rearranging the equation to isolate v21:
mv21=Kx20−Kx2−mv2
- Dividing by m:
v21=Km(x20−x2)−v2
- Taking the square root to find v1:
v1=√Km(x20−x2)−v2
The speed of the other particle is:
v1=√Km(x20−x2)−v2
Topper's Solved these Questions
- BOOK - FIITJEECHAPTER - WORK, ENERGY AND POWER EXERCISE - ASSIGNMENT PROBLEMS ( OBJECTIVE) (LEVEL-I)36videos
WORK, ENERGY AND POWER
- BOOK - FIITJEECHAPTER - WORK, ENERGY AND POWER EXERCISE - ASSIGNMENT PROBLEMS ( OBJECTIVE) (LEVEL-I) (ASSERTION REASONING TYPE)2videos
WORK, ENERGY AND POWER
- BOOK - FIITJEECHAPTER - WORK, ENERGY AND POWER EXERCISE - ASSIGNMENT PROBLEMS ( SUBJECTIVE) (LEVEL-I) Numerical8videos
WORK, ENERGY AND POWER
- BOOK - FIITJEECHAPTER - TEST PAPERSEXERCISE - PHYSICS747videos
TEST PAPERS
Similar Questions
Two blocks of masses m and m' are connected by a light spring on a horizontal frictionless table . The spring is compressed and then released . Find the ratio of acceleration of masses .
View SolutionTwo particles each of mass m are connected by a light inextensible string and a particle of mass M is attached to the midpoint of the string. The system is at rest on a smooth horizontal table with string just taut and in a straight line. The particle M is given a velocity v along the table perpendicular to the string. Prove that when the two particles are about to collide :
(i) The velocity of M is Mv(M+2m)
(ii) The speed of each of the other particles is (√2M(M+m)(M+2m))v.View Solution
Knowledge Check
- Question 1 - Select One
Two identical particle each of mass m are inter connects by a light spring of stiffness k ,the time period for small oscillation is equal to
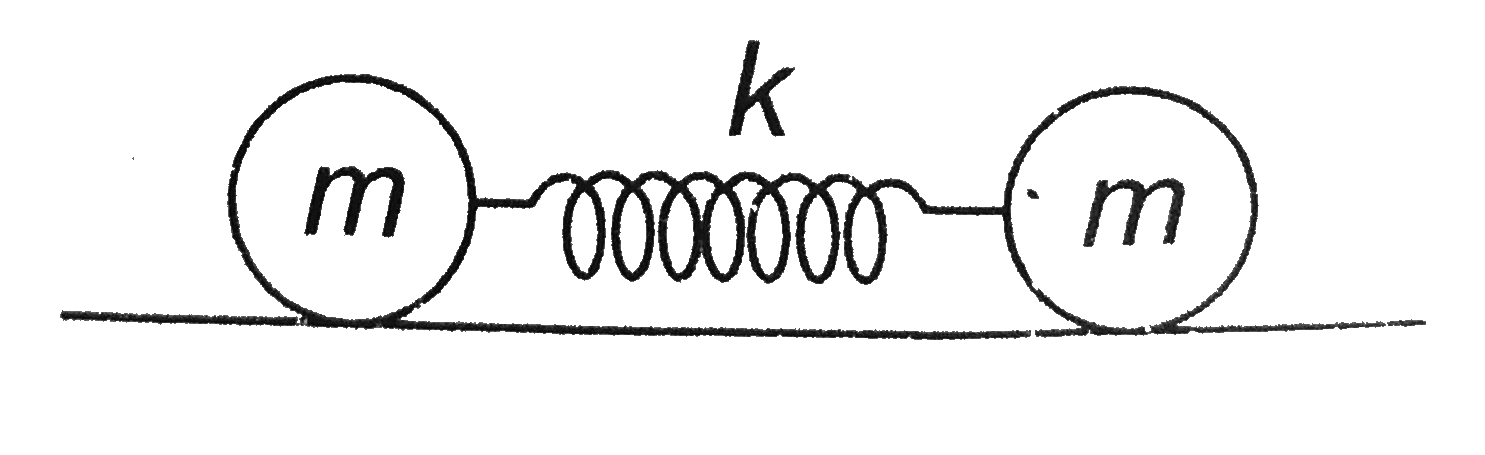 A2π√mkBπ2√mkCπ√m2kDπ√2mk
A2π√mkBπ2√mkCπ√m2kDπ√2mk - Question 2 - Select One
Two identical particles each of mass 0.5kg are interconnected by a light springs of stiffness 100N/m, time period of small oscillation is ….
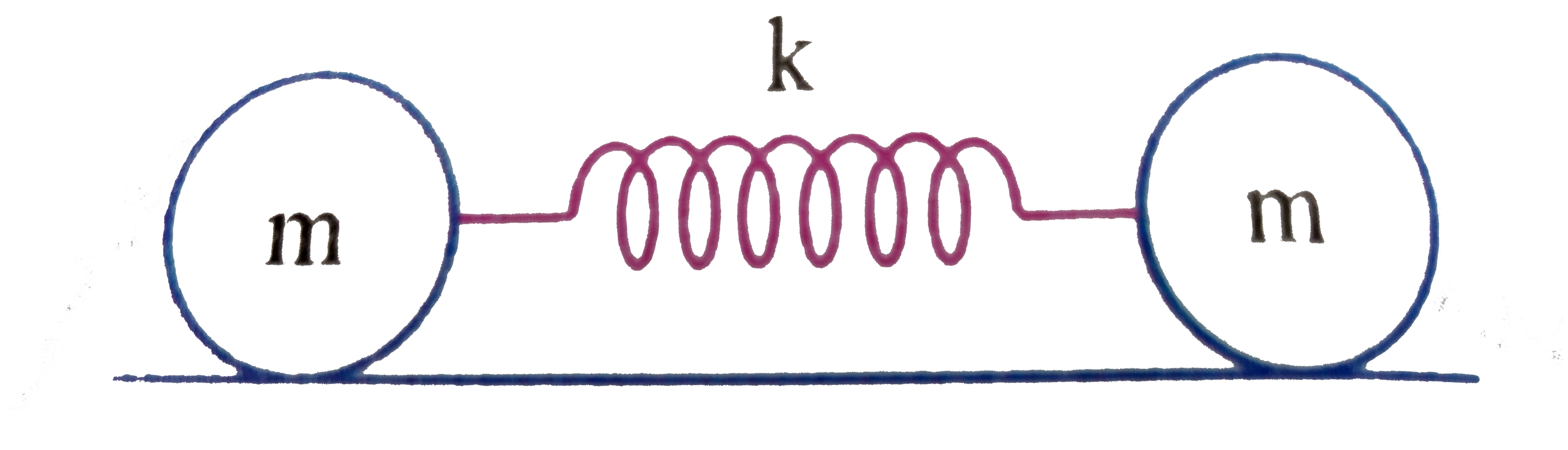 Aπ5√2Bπ10√2sCπ5sDπ10s
Aπ5√2Bπ10√2sCπ5sDπ10s - Question 3 - Select One
Two identicle particles A and B, each of mass m, are interconnected by a spring of stiffness k. If particle B experiences a forec F and the elongation of the spring is x, the acceleration of particle B relative to particle A is equal to
 AF2mBF−kxmCF−2kxmDkxm
AF2mBF−kxmCF−2kxmDkxm
A bullet of mass m strikes a block of mass M connected to a light spring of stiffness k, with a speed v0 and gets into it. Find the loss of K.E. of the bullet.
 View Solution
View SolutionA bullet of mass m strikes a block of mass M connected to a light spring of stiffness k, with a speed v0 and gets into it. Find the loss of K.E. of the bullet.
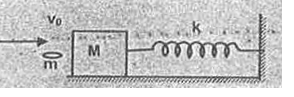 View Solution
View SolutionA sand bag of mass m is hanging from a light spring of stiffness k. Find the elongation of the spring. If we pull the sand bag down by an additional distance x and release it, find its acceleration and maximum velocity of block.
 View Solution
View SolutionIn an ideal pulley particle system, mass m2 is connected with a vertical spring of stiffness k. If mass m2 is released from rest, when the spring is underformed, find the maximum compression of the spring.
 View Solution
View SolutionTwo identical particles of charge q each are connected by a massless spring of force constant k. They are placed over a smooth horizontal surface. They are released when the separation between them is r and spring is unstretched. If maximum extension of the spring is r, the value of k is (neglect gravitational effect)
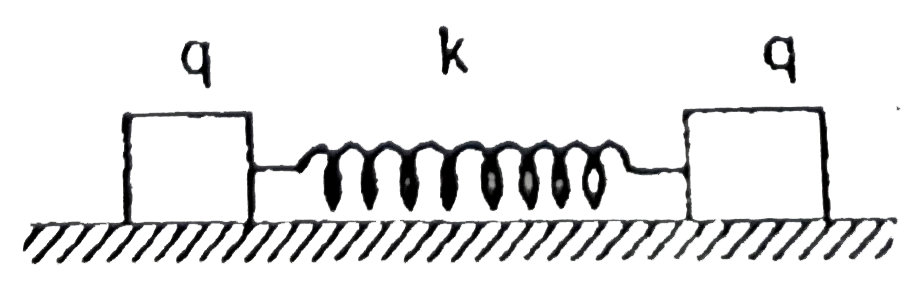 View Solution
View Solution

