In an ideal pulley particle system, mass m2 is connected with a vertical spring of stiffness k. If mass m2 is released from rest, when the spring is underformed, find the maximum compression of the spring.

The correct Answer is:2(m2−m1)gk
Since work done by the constrain forces, tension and normal reaction is zero. The mechanical energy of the system will be conserve
ΔME=0
or ΔK+ΔU=0

Let x be the maximum compression of the spring.
Then, ΔUsp=k2x2 (i)
As m1 descends by a distance x,
ΔUgr1=−m2gx(ii)
As m2 ascends by a distance x, ltbrrgt ΔUgr2=m2gx (iii)
Since, both m1 and m2 comes to rest simultaneously,
ΔK=0 (iv)
Conservation of energy: ΔK+ΔU=0
[ΔUsp+ΔUgr1+ΔUgr2]+ΔK=0
(12kx2+m1gx−m2gx)+0=0
⇒x=2(m2−m1)gk
Topper's Solved these Questions
- WORK, POWER & ENERGYBOOK - CENGAGE PHYSICSCHAPTER - WORK, POWER & ENERGYEXERCISE - Single Correct
100 Videos
- WORK, POWER & ENERGYBOOK - CENGAGE PHYSICSCHAPTER - WORK, POWER & ENERGYEXERCISE - Multiple Correct
25 Videos
- WORK, POWER & ENERGYBOOK - CENGAGE PHYSICSCHAPTER - WORK, POWER & ENERGYEXERCISE - Exercise 8.5
15 Videos
- VECTORSBOOK - CENGAGE PHYSICSCHAPTER - VECTORSEXERCISE - Exercise Multiple Correct
5 Videos
Similar Questions
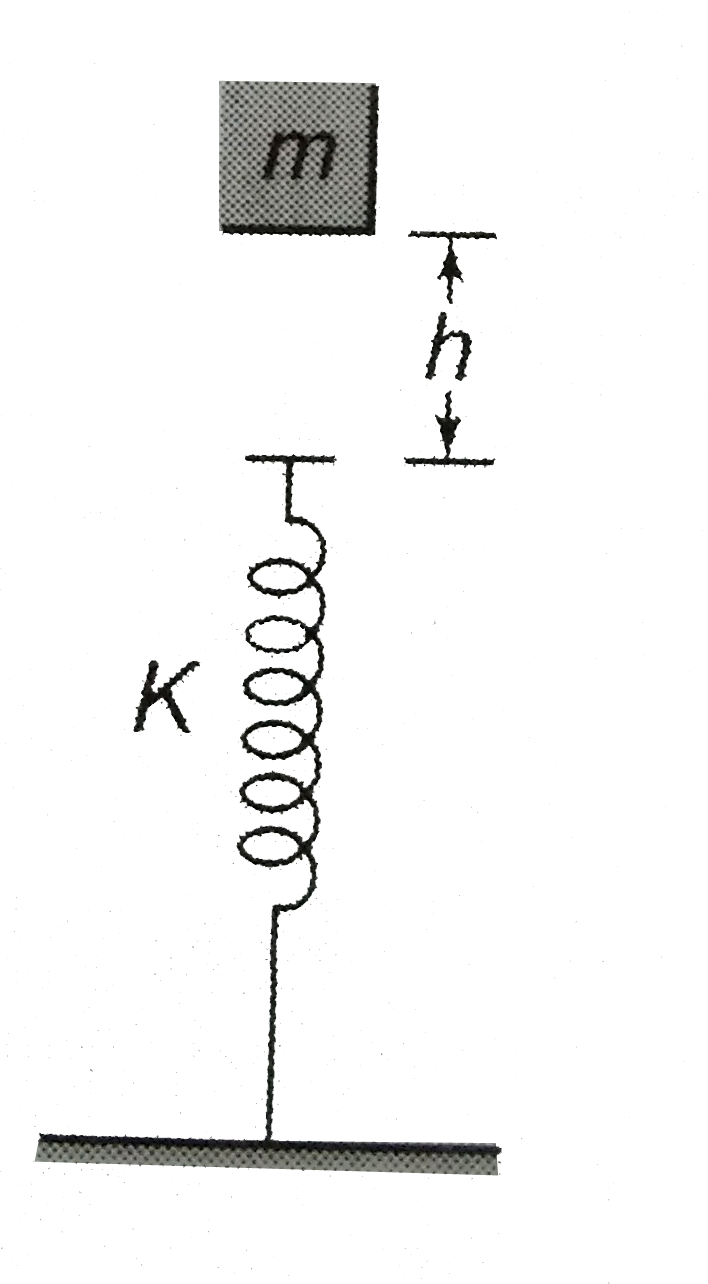
A block is released from height h, find the maximum compression of spring of spring constant k.
View SolutionA block of mass m strikes a light pan fitted with a vertical spring after falling through a distance h. If the stiffness of the spring is k, find the maximum compression of the spring.
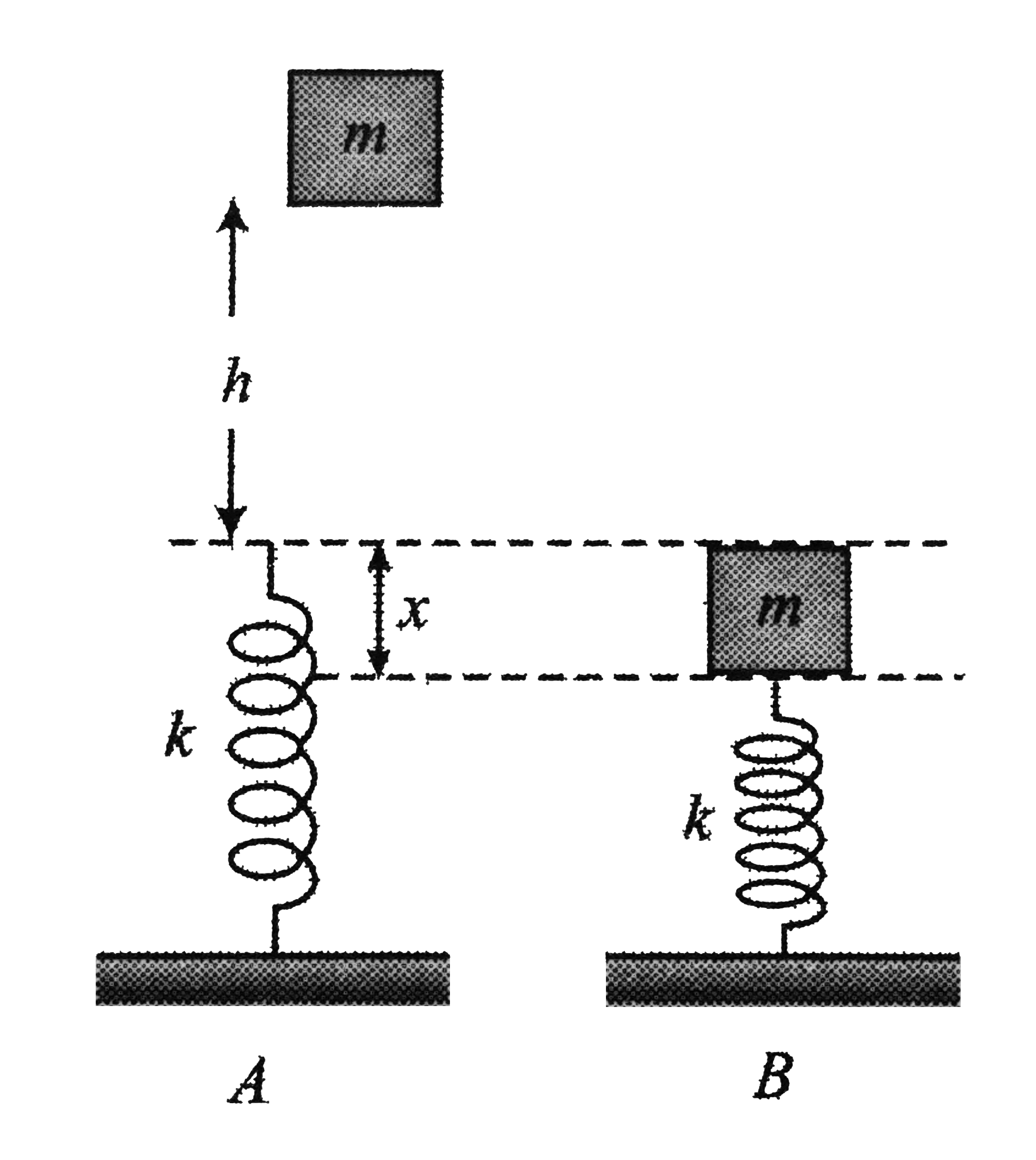
View Solution
Knowledge Check
A disc of mass m is connected with an ideal spring of stiffness k. If it is released from rest, it rolls without sliding on an inclination plane. The maximum elongation of the spring is:
 AmgsinθkB2mgsinθ3kC3mgsinθkD2mgsinθk
AmgsinθkB2mgsinθ3kC3mgsinθkD2mgsinθk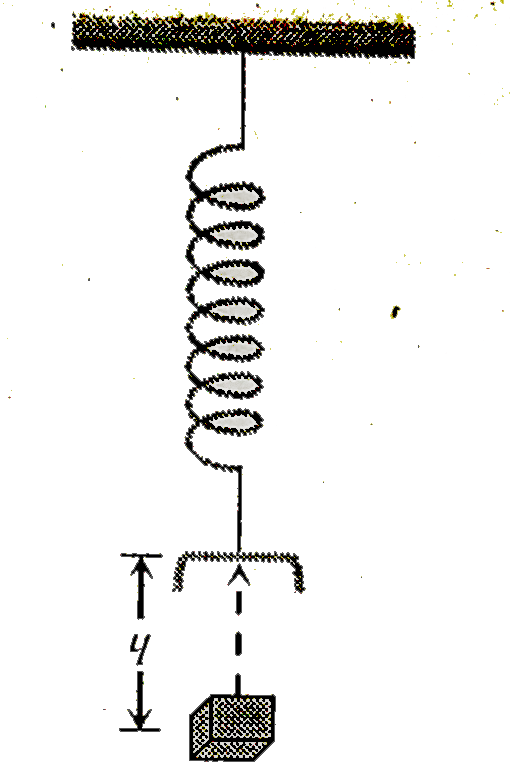
A block of mass m initially at rest is dropped from a height h on to a spring of force constant k . the maximum compression in the spring is x thenAmgh=12kx2Bmg(h+x)=12kx2Cmgh=12k(x+h)2Dmg(h+x)=12k(x+h)2A block of mass m attached in the lower and vertical spring The spring is hung from a calling and force constant value k The mass is released from rfest with the spring velocity unstrached The maximum value praduced in the length of the spring will be
AMg/kB2Mg/kC4Mg/kDMg/2k
A body of mass m hangs by an inextensible string that passes over a smooth mass less pulley that is fitted with a light spring of stiffness k as shown in figure. If the body is released from rest and the spring is released, calculate the maximum elongation of the spring.
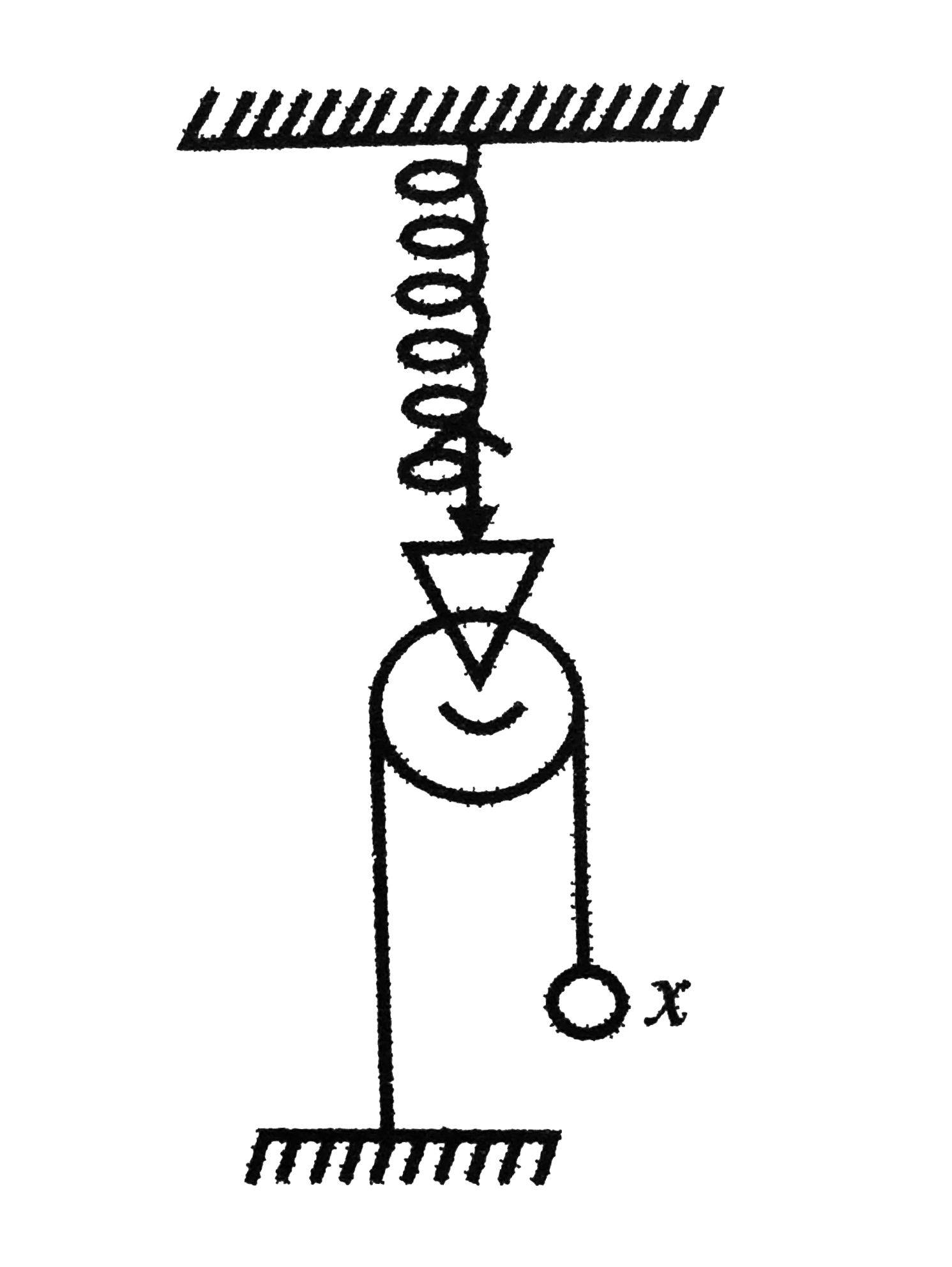
View SolutionA block of mass m connected with a smooth prismatic wedge of mass m is released from rest when the spring is relaxed. Find the angular frequency of oscillation.

View SolutionThe block of mass m is released when the spring was in its natrual length. Spring constant is k. Find the maximum elongation of the spring.

View SolutionA sphere of mass m and radius R rolls without sliding on a horizontal surface. It collides with a light spring of stiffness K with a kinetic energy E. If the surface (AB) under the spring is smooth, find the maximum compression of the spring.
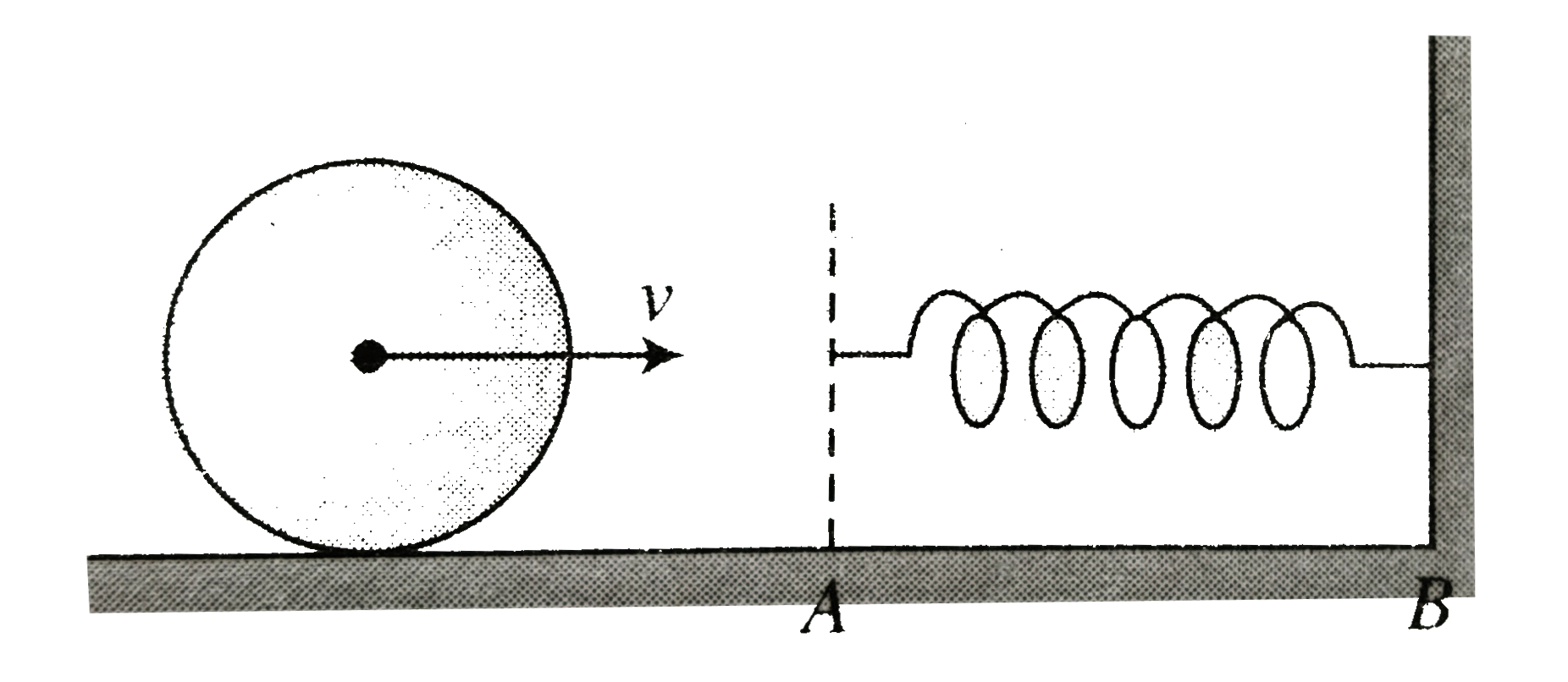
View SolutionTwo smooth blocks of mases m1andm2 attached with an ideal spring of stiffness k and kept on hrozontal surface. If m1 is projected with a horizontal velocity v0. Find the maximum compression of the spring.
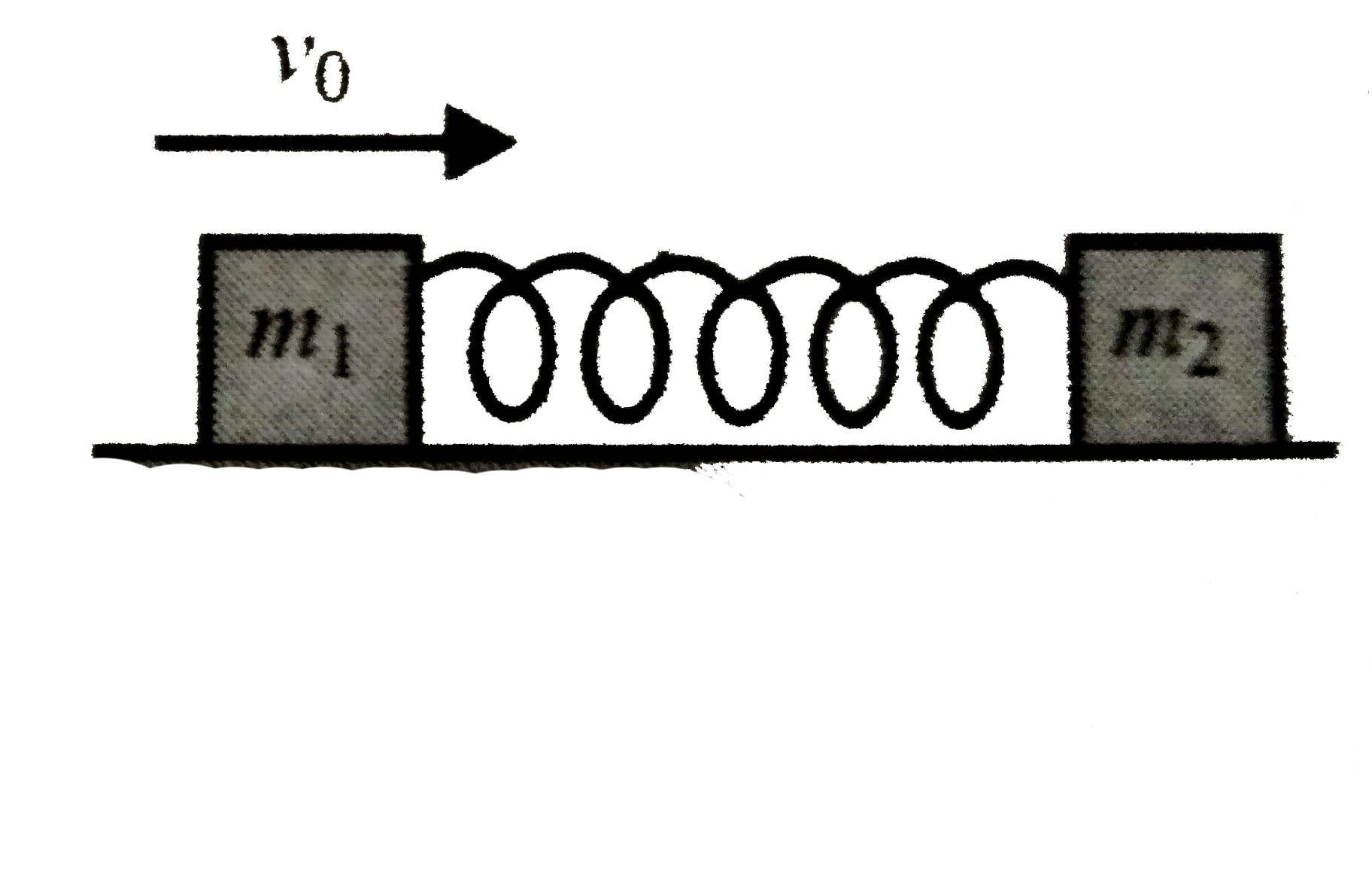
View Solution
