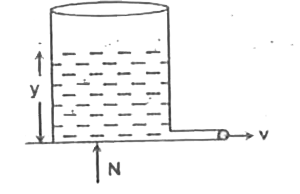
A light cylindrical vessel is kept on a horizontal surface it's base area is A. A hole of cross-sectional area a is made just at it's bottom side. The minimum coefficient of friction necessary for not sliding of vessel due to the impact force of the emerging liquid.
varying
a/A
2a/A
None of these
The velocity of efflux of the liquid is given as
v=√2gy
∴ The reaction force of the emerging liquid on the vessel + liquid content is equal to
F=vdmdt=vaρv=aρv2
⇒F=aρ(√2gy)2=2aρgy
⇒μN=2aρgy
⇒μ(Aρgy)=2aρgy
⇒μ=2aA
Hence (C ) is correct
Topper's Solved these Questions
- BOOK - FIITJEECHAPTER - FLUID MECHANICS EXERCISE - LINKED COMPREHENSION TYPE2videos
FLUID MECHANICS
- BOOK - FIITJEECHAPTER - FLUID MECHANICS EXERCISE - LINKED COMPREHENSION TYPE I1videos
FLUID MECHANICS
- BOOK - FIITJEECHAPTER - FLUID MECHANICS EXERCISE - SOLVED PROBLEMS (SUBJECTIVE)10videos
FLUID MECHANICS
- BOOK - FIITJEECHAPTER - ELECTROSTATICSEXERCISE - Example14videos
ELECTROSTATICS
- BOOK - FIITJEECHAPTER - GENERAL PHYSICSEXERCISE - MATRIX MATCH TYPE3videos
GENERAL PHYSICS
Similar Questions
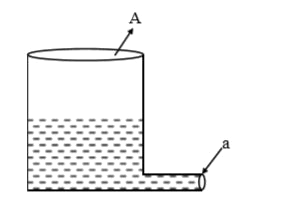
A light cylindrical vessel is kept on a horizontal surface. Area of base is A. A hole of crosssectional area 'a' is made just at its bottom side. The minimum coefficient of friction necessary to prevent sliding the vessel due to the impact force of the emerging liquid is (a<<A):
 View Solution
View SolutionA light cylindrical vessel is kept on a horizontal surface. Its base area is A. a hole of cross sectional area a is made just at its bottom sdie (where a ltlt A). Find minimum coefficeint of friction necessary for sliding of the vesssel due to the impact force of the emerging liquid.
 View Solution
View Solution
Knowledge Check
- Question 1 - Select One
A cylindrical vessel filled with water upto a height of 2m stands on horizontal plane. The side wall of the vessel has a pugged circular hole touching the bottom. If the minimum diameter of the hole so that the vessel begins to move on the floor if the plug is removed is x10√π meter then x will be (if the coefficient of frication between the bottom of the vessel and the plane is 0.4 and total mass of water plus vessel is 100kg.)
A√2μMπρHB√μM2πρHC√μMρHDnone - Question 2 - Select One
In the figure shown, a light container is kept on a horizontal rough surface of coefficient of friction μ=ShV. A very small hole of area S is made at depth 'h'. Water of volume 'V' is filled in the container. The friction is not sufficient to keep the container at rest. The acceleration of the container initially is
 AVShgBgCzeroDShVg
AVShgBgCzeroDShVg - Question 3 - Select One
A cubical block of side L rests on a rough horizontal surface with coefficient of friction μ. A horizontal force F is applied on the block as shown. If the coefficient of frictions sufficienty high so that the block does not slide before toppling, the minimum force required to topple the block is :
 . AinfinitesimalBmg/4Cmg/2Dmg(1−μ)
. AinfinitesimalBmg/4Cmg/2Dmg(1−μ)
A light cylindrical vessel is kept on a horizontal surface. Its base area is A. a hole of cross sectional area a is made just at its bottom side (where a less than A). Find minimum coefficeint of friction necessary for sliding of the vesssel due to the impact force of the emerging liquid.
 View Solution
View SolutionA rod of length L kept on a smooth horizontal surface is pulled along its length by a force F. The area of cross-section is A and Young's modulus is Y. The extension in the rod is
 View Solution
View SolutionA cylindrical vessel of area of cross section A is filled with a liquid up to a height H. A very small hole of area of cross section a is made at the bottom of the vellel. Find the time taken by the vessel to become empty.
View SolutionA cubical block of side L rests on a rough horizonta surface with coefficient of friction μ. A horizontal force F is applied on the block as shown. If the coefficient of friction is sufficiently high so that the block does not slide before toppling, the minimum force required to topple the block is
 View Solution
View SolutionA cylindrical vessel open at the top is 20cm high and 10cm in diameter. A circular hole of cross-sectional area 1cm2 is cut at the centre of the bottom of the vessel. Water flows from a tube above it into the vessel at the rate of 102cm3/s. The height of water in the vessel under steady state is (Take g=10m/s2).
View Solution

