Consider the parallel resonant circuit shown in adjacent figure. One branch contains an inductor of inductance L and a small ohmic resistance R, whereas the other branch contains a capacitor of capacitance C. The circuit is fed by a source of alternating emfE=Eoejωt=Eosinωt
The impedance of inductor branch, Z(1)=R+jωL
The impendence of capacitor branch, Z(2) = (1//jomegaC)therefourNetimpedanceZofthetwoparal≤lbranchesisgivenby<br>(1)/(Z)=(1)/(Z_(1))+ (1)/)Z_(2)=(1)/(R+jomegaC<br>=(R-jomegaL)/(jomegaL)(R-jomegaL)+jomegaC=(R)/(R^(2)+omega^(2)+L^(2))+jomega[C-(L)/(R^(2)+omegaL^(2))]<br>Thecurrentflow∈g∈the∘uit<br>I=(E)/(Z)=(E)[(R)/(R^(2)+omega^(2)L^(2))+jomega(C-(L)/(R^(2)+omega^(2)L^(2)))]<br>Forresonance→our,thecurrentμstbe∈phasewiththeappliedemf.Forthis,thereactivecompo≠ntofcurrentshod––bezero,l.e.<br>omega[C-(L)/(R^(2)+omega^(2)L^(2))]=0<br>orC=(L)/(R^(2)+omega_(r)^(2)L^(2))(writ∈gomega_(r)foromegaatresonance)<br>Thisgivesresonantanga––requency<br>omega_(r)=sqrt((1)/(LC)-R^(2)/(L^(2)))Atparal≤l∘uitresonance,theimpendenceismaxiμmandcurrentisminiμm.Paral≤lresonant∘uitissome×cal≤dtheanti−resonance∈order→dist∈guishomseriesresonance<br>QF∈dtheimpedanceofAC∘uitatresonanceshown∈theadjacentfigure<br><imga≤ocr_imageload∈g=lazysrc=https://d10lpgp6xz60nq.cloudfront.net/physics_images/FIITJEE_PHY_MB_06_C03_E04_003_Q01.pngwh=80%mx-autosty≤=background:white;><br>Foranac∘uit,impendenceisgivenbyZ = 50 + jK(P^(2) - 4Q^(2), where K is a positive non-. zero constant. For resonance, which of the following expression is true
P =2 Q
P =Q
P+Q=K
P-Q=K
The correct Answer is:A
Topper's Solved these Questions
- AC CIRCUITSBOOK - FIITJEECHAPTER - AC CIRCUITSEXERCISE - COMPREHENSION-(II)( Assuming that any resistance of inductor is included in R, answer the following question)
10 Videos
- AC CIRCUITSBOOK - FIITJEECHAPTER - AC CIRCUITSEXERCISE - ASSERTION REASONING TYPE
1 Videos
- AC CIRCUITSBOOK - FIITJEECHAPTER - AC CIRCUITSEXERCISE - ASSIGNMENT PROBLEMS(OBJECTIVELevel - Il)
14 Videos
- COLLISION BOOK - FIITJEECHAPTER - COLLISION EXERCISE - (NUMERICAL BASED QUESTIONS)
4 Videos
Similar Questions
If resistance R =100 Omega, inductance L = 12mH and capacitance C=15muF are connected in series to an AC sources, then at resonance the impedance of circuit is
View SolutionConsider the parallel resonant circuit shown in adjacent figure. One branch contains an inductor of inductance L and a small ohmic resistance R, whereas the other branch contains a capacitor of capacitance C. The circuit is fed by a source of alternating emfE=Eoejωt=Eosinωt
The impedance of inductor branch, Z(1)=R+jωL
The impendence of capacitor branch, Z(2) = (1//jomegaC)therefourNetimpedanceZofthetwoparal≤lbranchesisgivenby<br>(1)/(Z)=(1)/(Z_(1))+ (1)/)Z_(2)=(1)/(R+jomegaC<br>=(R-jomegaL)/(jomegaL)(R-jomegaL)+jomegaC=(R)/(R^(2)+omega^(2)+L^(2))+jomega[C-(L)/(R^(2)+omegaL^(2))]<br>Thecurrentflow∈g∈the∘uit<br>I=(E)/(Z)=(E)[(R)/(R^(2)+omega^(2)L^(2))+jomega(C-(L)/(R^(2)+omega^(2)L^(2)))]<br>Forresonance→our,thecurrentμstbe∈phasewiththeappliedemf.Forthis,thereactivecompo≠ntofcurrentshod––bezero,l.e.<br>omega[C-(L)/(R^(2)+omega^(2)L^(2))]=0<br>orC=(L)/(R^(2)+omega_(r)^(2)L^(2))(writ∈gomega_(r)foromegaatresonance)<br>Thisgivesresonantanga––requency<br>omega_(r)=sqrt((1)/(LC)-R^(2)/(L^(2))) At parallel circuit resonance, theimpendence is maximum and current is minimum. Parallel resonant circuit is sometimes called the anti-resonance in order to distinguish from series resonance
QFind the impedance of AC circuit at resonance shown in the adjacent figure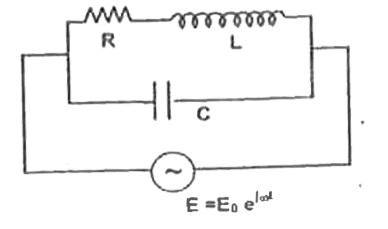
A coil of inductance 100 muH and 60 Omega effective resistance is connected in parallel with a condenser of 100 pF. The resonant circuit so formed is excited from an alternating current source. The frequency of the source is varied until the maximum impendence of the circuit is obtained. The frequency of the generator at which this occurs is approximately
View Solution
Knowledge Check
Consider the parallel resonant circuit shown in adjacent figure. One branch contains an inductor of inductance L and a small ohmic resistance R, whereas the other branch contains a capacitor of capacitance C. The circuit is fed by a source of alternating emfE=Eoejωt=Eosinωt
The impedance of inductor branch, Z(1)=R+jωL
The impendence of capacitor branch, Z(2) = (1//jomegaC)therefourNetimpedanceZofthetwoparal≤lbranchesisgivenby<br>(1)/(Z)=(1)/(Z_(1))+ (1)/)Z_(2)=(1)/(R+jomegaC<br>=(R-jomegaL)/(jomegaL)(R-jomegaL)+jomegaC=(R)/(R^(2)+omega^(2)+L^(2))+jomega[C-(L)/(R^(2)+omegaL^(2))]<br>Thecurrentflow∈g∈the∘uit<br>I=(E)/(Z)=(E)[(R)/(R^(2)+omega^(2)L^(2))+jomega(C-(L)/(R^(2)+omega^(2)L^(2)))]<br>Forresonance→our,thecurrentμstbe∈phasewiththeappliedemf.Forthis,thereactivecompo≠ntofcurrentshod––bezero,l.e.<br>omega[C-(L)/(R^(2)+omega^(2)L^(2))]=0<br>orC=(L)/(R^(2)+omega_(r)^(2)L^(2))(writ∈gomega_(r)foromegaatresonance)<br>Thisgivesresonantanga––requency<br>omega_(r)=sqrt((1)/(LC)-R^(2)/(L^(2))) At parallel circuit resonance, theimpendence is maximum and current is minimum. Parallel resonant circuit is sometimes called the anti-resonance in order to distinguish from series resonance
QFind the impedance of AC circuit at resonance shown in the adjacent figure
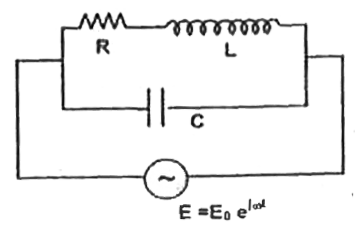
Find the impedance of AC circuit at resonance shown in the adjacent figure
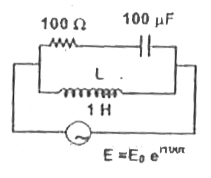 A100√2ΩB200ΩC100ΩD200√2√
A100√2ΩB200ΩC100ΩD200√2√Consider the parallel resonant circuit shown in adjacent figure. One branch contains an inductor of inductance L and a small ohmic resistance R, whereas the other branch contains a capacitor of capacitance C. The circuit is fed by a source of alternating emfE=Eoejωt=Eosinωt
The impedance of inductor branch, Z(1)=R+jωL
The impendence of capacitor branch, Z(2) = (1//jomegaC)therefourNetimpedanceZofthetwoparal≤lbranchesisgivenby<br>(1)/(Z)=(1)/(Z_(1))+ (1)/)Z_(2)=(1)/(R+jomegaC<br>=(R-jomegaL)/(jomegaL)(R-jomegaL)+jomegaC=(R)/(R^(2)+omega^(2)+L^(2))+jomega[C-(L)/(R^(2)+omegaL^(2))]<br>Thecurrentflow∈g∈the∘uit<br>I=(E)/(Z)=(E)[(R)/(R^(2)+omega^(2)L^(2))+jomega(C-(L)/(R^(2)+omega^(2)L^(2)))]<br>Forresonance→our,thecurrentμstbe∈phasewiththeappliedemf.Forthis,thereactivecompo≠ntofcurrentshod––bezero,l.e.<br>omega[C-(L)/(R^(2)+omega^(2)L^(2))]=0<br>orC=(L)/(R^(2)+omega_(r)^(2)L^(2))(writ∈gomega_(r)foromegaatresonance)<br>Thisgivesresonantanga––requency<br>omega_(r)=sqrt((1)/(LC)-R^(2)/(L^(2)))Atparal≤l∘uitresonance,theimpendenceismaxiμmandcurrentisminiμm.Paral≤lresonant∘uitissome×cal≤dtheanti−resonance∈order→dist∈guishomseriesresonance<br>QF∈dtheimpedanceofAC∘uitatresonanceshown∈theadjacentfigure<br><imga≤ocr_imageload∈g=lazysrc=https://d10lpgp6xz60nq.cloudfront.net/physics_images/FIITJEE_PHY_MB_06_C03_E04_002_Q01.pngwh=80%mx-autosty≤=background:white;><br>Thereactanceofthe∘uit∈theadjacentfigureis20Ω.F∈dthevalueofI_(rms)
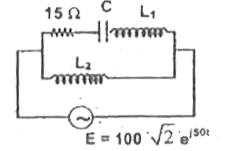 A4 AmpB2 AmpC4.5 AmpD13.5 Amp
A4 AmpB2 AmpC4.5 AmpD13.5 AmpConsider the parallel resonant circuit shown in adjacent figure. One branch contains an inductor of inductance L and a small ohmic resistance R, whereas the other branch contains a capacitor of capacitance C. The circuit is fed by a source of alternating emfE=Eoejωt=Eosinωt
The impedance of inductor branch, Z(1)=R+jωL
The impendence of capacitor branch, Z(2) = (1//jomegaC)therefourNetimpedanceZofthetwoparal≤lbranchesisgivenby<br>(1)/(Z)=(1)/(Z_(1))+ (1)/)Z_(2)=(1)/(R+jomegaC<br>=(R-jomegaL)/(jomegaL)(R-jomegaL)+jomegaC=(R)/(R^(2)+omega^(2)+L^(2))+jomega[C-(L)/(R^(2)+omegaL^(2))]<br>Thecurrentflow∈g∈the∘uit<br>I=(E)/(Z)=(E)[(R)/(R^(2)+omega^(2)L^(2))+jomega(C-(L)/(R^(2)+omega^(2)L^(2)))]<br>Forresonance→our,thecurrentμstbe∈phasewiththeappliedemf.Forthis,thereactivecompo≠ntofcurrentshod––bezero,l.e.<br>omega[C-(L)/(R^(2)+omega^(2)L^(2))]=0<br>orC=(L)/(R^(2)+omega_(r)^(2)L^(2))(writ∈gomega_(r)foromegaatresonance)<br>Thisgivesresonantanga––requency<br>omega_(r)=sqrt((1)/(LC)-R^(2)/(L^(2))) At parallel circuit resonance, theimpendence is maximum and current is minimum. Parallel resonant circuit is sometimes called the anti-resonance in order to distinguish from series resonance
QFind the impedance of AC circuit at resonance shown in the adjacent figure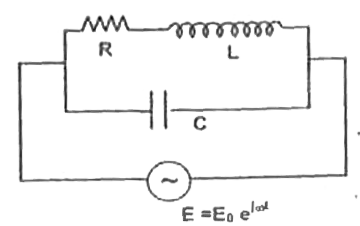
Which of the following graph shows correct relation beteen current I and frequency f in a parallel AC circuitA B
B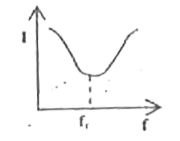 C
C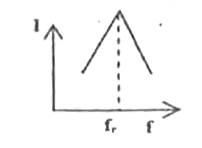 D
D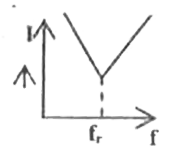
An L-C_R series circuit is joined to a source of alternating e.m.f. If R=9Ω,XL=28Ω,XC=16Ω, then the impedance of the circuit will be
View SolutionThe current flowing in two branches of parallel resonant circuit at resonance are
View SolutionThe value of impedance in parallel LC circuit at resonance is (assuming inductor and capacitor to be ideal)
View SolutionThe impedance of a circuit, when a resistance R and an inductor of inductance are connected in series in an AC circuit of frequency f is
View SolutionIf resistance R =100 Omega, inductance L = 12mH and capacitance C=15muF are connected in series to an AC sources, then at resonance the impedance of circuit is
View Solution
