The det Δ=∣∣ ∣ ∣∣d2+rdedfdee2+refdfeff2+r∣∣ ∣ ∣∣ is divisible by
r2
(d+e2+f2+r)
(d2+e2+f2+r)
(d2+e+f2+r2)
The correct Answer is:C
To solve the determinant Δ=∣∣
∣
∣∣d2+rdedfdee2+refdfeff2+r∣∣
∣
∣∣, we will follow these steps:
Step 1: Write down the determinant
We start with the determinant:
Δ=∣∣
∣
∣∣d2+rdedfdee2+refdfeff2+r∣∣
∣
∣∣
Step 2: Expand the determinant using cofactor expansion
We can expand the determinant along the first row:
Δ=(d2+r)∣∣∣e2+refeff2+r∣∣∣−de∣∣∣deefdff2+r∣∣∣+df∣∣∣dee2+rdfef∣∣∣
Step 3: Calculate the 2x2 determinants
1. Calculate ∣∣∣e2+refeff2+r∣∣∣:
=(e2+r)(f2+r)−(ef)(ef)=e2f2+re2+rf2+r2−e2f2=re2+rf2+r2
2. Calculate ∣∣∣deefdff2+r∣∣∣:
=(de)(f2+r)−(ef)(df)=def2+der−efd2
3. Calculate ∣∣∣dee2+rdfef∣∣∣:
=(de)(ef)−(e2+r)(df)=def−e2df−rdf
Step 4: Substitute back into the determinant
Substituting these results back into the expression for Δ:
Δ=(d2+r)(re2+rf2+r2)−de(def2+der−efd2)+df(def−e2df−rdf)
Step 5: Simplify the expression
Now we simplify Δ:
Δ=(d2+r)(re2+rf2+r2)−(def2de+derde−de2fd)+(def2−e2df2−rdf2)
Step 6: Collect like terms
After collecting like terms, we find:
Δ=r(d2+e2+f2+r)+(other terms that cancel out)
Step 7: Factor out common terms
From our simplification, we can factor out r2:
Δ=r2+r(d2+e2+f2)
Conclusion
Thus, we conclude that the determinant Δ is divisible by r2.
∣
∣∣d2+rdedfdee2+refdfeff2+r∣∣
∣
∣∣, we will follow these steps:
We start with the determinant:
Δ=∣∣
∣
∣∣d2+rdedfdee2+refdfeff2+r∣∣
∣
∣∣
We can expand the determinant along the first row:
Δ=(d2+r)∣∣∣e2+refeff2+r∣∣∣−de∣∣∣deefdff2+r∣∣∣+df∣∣∣dee2+rdfef∣∣∣
1. Calculate ∣∣∣e2+refeff2+r∣∣∣:
=(e2+r)(f2+r)−(ef)(ef)=e2f2+re2+rf2+r2−e2f2=re2+rf2+r2
=(de)(f2+r)−(ef)(df)=def2+der−efd2
=(de)(ef)−(e2+r)(df)=def−e2df−rdf
Substituting these results back into the expression for Δ:
Δ=(d2+r)(re2+rf2+r2)−de(def2+der−efd2)+df(def−e2df−rdf)
Now we simplify Δ:
Δ=(d2+r)(re2+rf2+r2)−(def2de+derde−de2fd)+(def2−e2df2−rdf2)
After collecting like terms, we find:
Δ=r(d2+e2+f2+r)+(other terms that cancel out)
From our simplification, we can factor out r2:
Δ=r2+r(d2+e2+f2)
Thus, we conclude that the determinant Δ is divisible by r2.
Topper's Solved these Questions
- DETERMINANTBOOK - FIITJEECHAPTER - DETERMINANTEXERCISE - EXERCIESE 1
3 Videos
- DETERMINANTBOOK - FIITJEECHAPTER - DETERMINANTEXERCISE - EXERCIESE 2
2 Videos
- DETERMINANTBOOK - FIITJEECHAPTER - DETERMINANTEXERCISE - SOLVED PROBLEMS (SUBJECTIVE)
7 Videos
- DEFINITE INTEGRAL BOOK - FIITJEECHAPTER - DEFINITE INTEGRAL EXERCISE - NUMERICAL BASED
3 Videos
- ELLIPSEBOOK - FIITJEECHAPTER - ELLIPSEEXERCISE - NUMERICAL BASED
4 Videos
Similar Questions
Suppose a,b,c,d,eandf are in G.P with common ratio >1. Let p.q.r be three real numbers. Let Δ=∣∣ ∣ ∣∣ad2pb2e2qc2fr∣∣ ∣ ∣∣. Then Δ depends on
View SolutionInstead of the usual definition of derivative Df(x), if we define a new kind of derivative D⋅F(x) by the formula D⋅f(x)=limh→0f2(x+h)−f2(x)h,wheref2(x) mean [f(x)]2 and if f(x)=xlogx ,then D⋅f(x)∣x=e has the value (A)e (B) 2e (c) 4e (d) none of these
View Solution
Knowledge Check
If the triangle ABC and DEF follows the given equation, then these two triangles are similar by which of the following criterion?
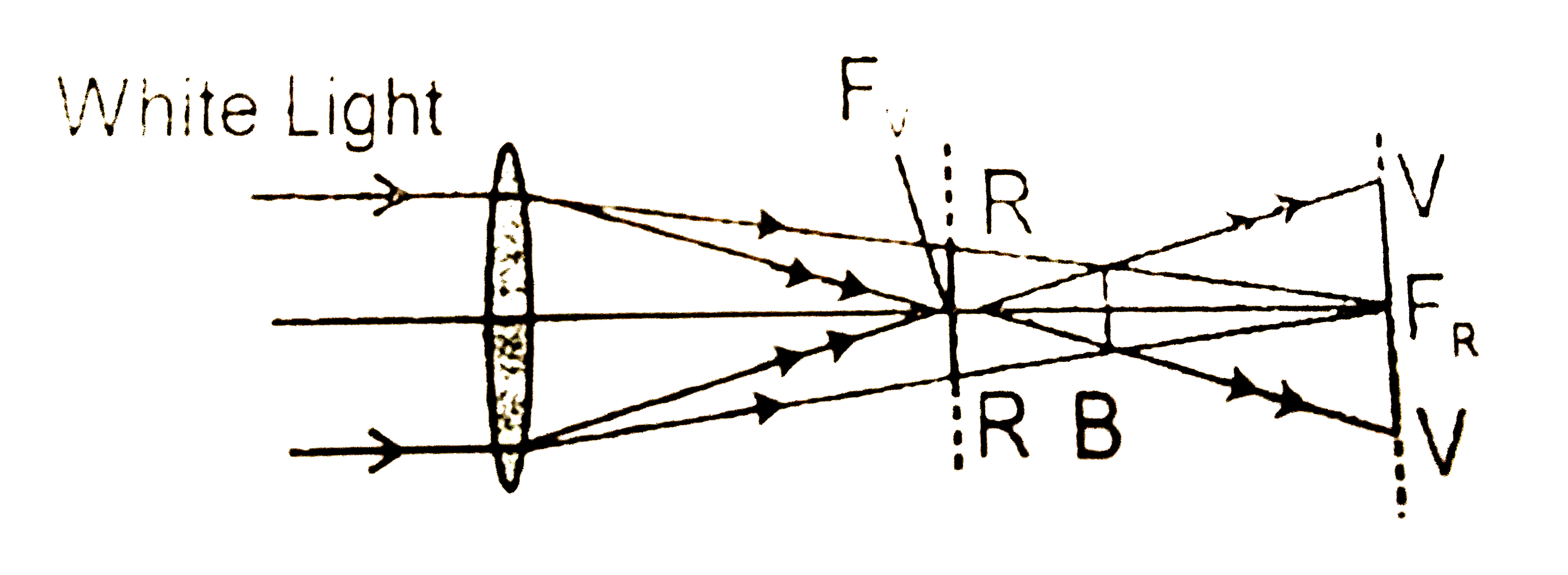
ABDE=BCEF=ACDFASAS similarityBAAA SimilarityCSSS SimilarityDNone of theseThe image of a white object in with light formed by a lens is usually colored and blurred. This defect of image is called chromatic aberration and arises due to the fact that focal length of a lens is different for different colours. As R .I. μ of lens is maximum for violet while minimum for red, violet is focused nearest to the lens while red farthest from it as shown in figure.
As a result of this, in case of convergent lens if a screen is placed at Fv center of the image will be violet and focused while sides are red and blurred. While at FR , reverse is the case, i.e ., center will be red and focused while sides violet and blurred. The differece between fv and fR is a measure of the longitudinal chromatic aberration (L.C.A),i.e.,
L.C.A.=fR−fv=−df with df=fv−fR ...........(1)
However, as for a single lens,
1f=(μ−1)[1R1−1R2] .............(2)
⇒−dff2=dμ[1R1−1R2] ...............(3)
Dividing E1n. (3) by (2) :
−dff=dμ(μ−1)=ω,[ω=dμ(μ−1)]dispersive power,.........(4)
And hence, from Eqns. (1) and (4) ,
L.C.A.=−df=ωf
Now, as for a single lens neither f nor ω zero, we cannot have a single lens free from chromatic aberration.
Condition of Achromatism :
In case of two thin lenses in contact
1F=1F1+1F2i.c,.−dFF2=df1f21−df2f22
The combination will be free from chromatic aberration if dF=0
i.e.,df1f21+df2f22=0 which with the help of Eqn. (4) reduces to
ω1f1f21+ω2f2f22=0,i.e.,ω1f1+ω2f2=0........(5)
This condition is called condition of achromatism (for two thin lenses in contact ) and the lens combination which satisfies this condition is called achromatic lems, from this condition, i.e., form Eqn. (5) it is clear the in case of achromatic doublet :
Since, if ω1=ω2,1f1+1f2=0i.e.,1F=0 or F=∞
i.e., combination will not behave as a lens, but as a plane glass plate.
(2) As ω1 and ω2 are positive quantities, for equation (5) to hold, f1 and f2 must be of opposite nature, i.e., if one of the lenses is converging the other must be diverging.
(3) If the achromatic combination is convergent,
fC<fD and as fCfd=ωCωD,ωC<ωd
i.e., in a convergent achromatic doublet, convex lens has lesses focal legth and dispersive power than the divergent one.
A combination is made of two lenses of focal lengths f and f' in contact , the dispersive powers of the materials of the lenses are ω and ω' . The combination is achromatic when :Aω=ω0,ω'=2ω0,f'=2fBω=ω0,ω'=2ω0,f'=f/2Cω=ω0,ω'=2ω0,f'=−f/2Dω=ω0, ω'=2ω0,f'=−2fThe image of a white object in with light formed by a lens is usually colored and blurred. This defect of image is called chromatic aberration and arises due to the fact that focal length of a lens is different for different colours. As R .I. μ of lens is maximum for violet while minimum for red, violet is focused nearest to the lens while red farthest from it as shown in figure.
As a result of this, in case of convergent lens if a screen is placed at Fv center of the image will be violet and focused while sides are red and blurred. While at FR , reverse is the case, i.e ., center will be red and focused while sides violet and blurred. The differece between fv and fR is a measure of the longitudinal chromatic aberration (L.C.A),i.e.,
L.C.A.=fR−fv=−df with df=fv−fR ...........(1)
However, as for a single lens,
1f=(μ−1)[1R1−1R2] .............(2)
⇒−dff2=dμ[1R1−1R2] ...............(3)

Dividing E1n. (3) by (2) :
−dff=dμ(μ−1)=ω,[ω=dμ(μ−1)]dispersive power,.........(4)
And hence, from Eqns. (1) and (4) ,
L.C.A.=−df=ωf
Now, as for a single lens neither f nor ω zero, we cannot have a single lens free from chromatic aberration.
Condition of Achromatism :
In case of two thin lenses in contact
1F=1F1+1F2i.c,.−dFF2=df1f21−df2f22
The combination will be free from chromatic aberration if dF=0
i.e.,df1f21+df2f22=0 which with the help of Eqn. (4) reduces to
ω1f1f21+ω2f2f22=0,i.e.,ω1f1+ω2f2=0........(5)
This condition is called condition of achromatism (for two thin lenses in contact ) and the lens combination which satisfies this condition is called achromatic lems, from this condition, i.e., form Eqn. (5) it is clear the in case of achromatic doublet :
Since, if ω1=ω2,1f1+1f2=0i.e.,1F=0 or F=∞
i.e., combination will not behave as a lens, but as a plane glass plate.
(2) As ω1 and ω2 are positive quantities, for equation (5) to hold, f1 and f2 must be of opposite nature, i.e., if one of the lenses is converging the other must be diverging.
(3) If the achromatic combination is convergent,
fC<fD and as fCfd=ωCωD,ωC<ωd
i.e., in a convergent achromatic doublet, convex lens has lesses focal legth and dispersive power than the divergent one.
Chromatic aberration of a lens can be corrected by :Aproviding different suitable curvatures of its two surfaces.Bproper polishing of its two surfaces.Csuitably conbining it with another lens.Dreducing its aperture.
people living at Mars ,instead of the usual definition of derivative Df(x) define a new kind of derivative Df(x) by the formula Df(x)=limh→0f2(x+h)−f2(x)h where fx means [f(x)]2. If f(x)=xInx then Df(x)∣x=e has the value (a) e (b) 2e (c) 4e (d) non
View SolutionIn the given figure, ABC is an equilateral triangle which is inscribed inside a circle and whose radius is r . Which of the following is the area of the triangle? (r+DE)12(r−DE)32 (b) (r−DE)12(r+DE)2 (c) (r−DE)2(r+DE)2 (d) (r−DE)12(r+DE)32
View SolutionIn figure, seg EF is a diameter and seg DF is a tangent segment. The radius of the circle is r. Prove that, DE×GE=4r2.
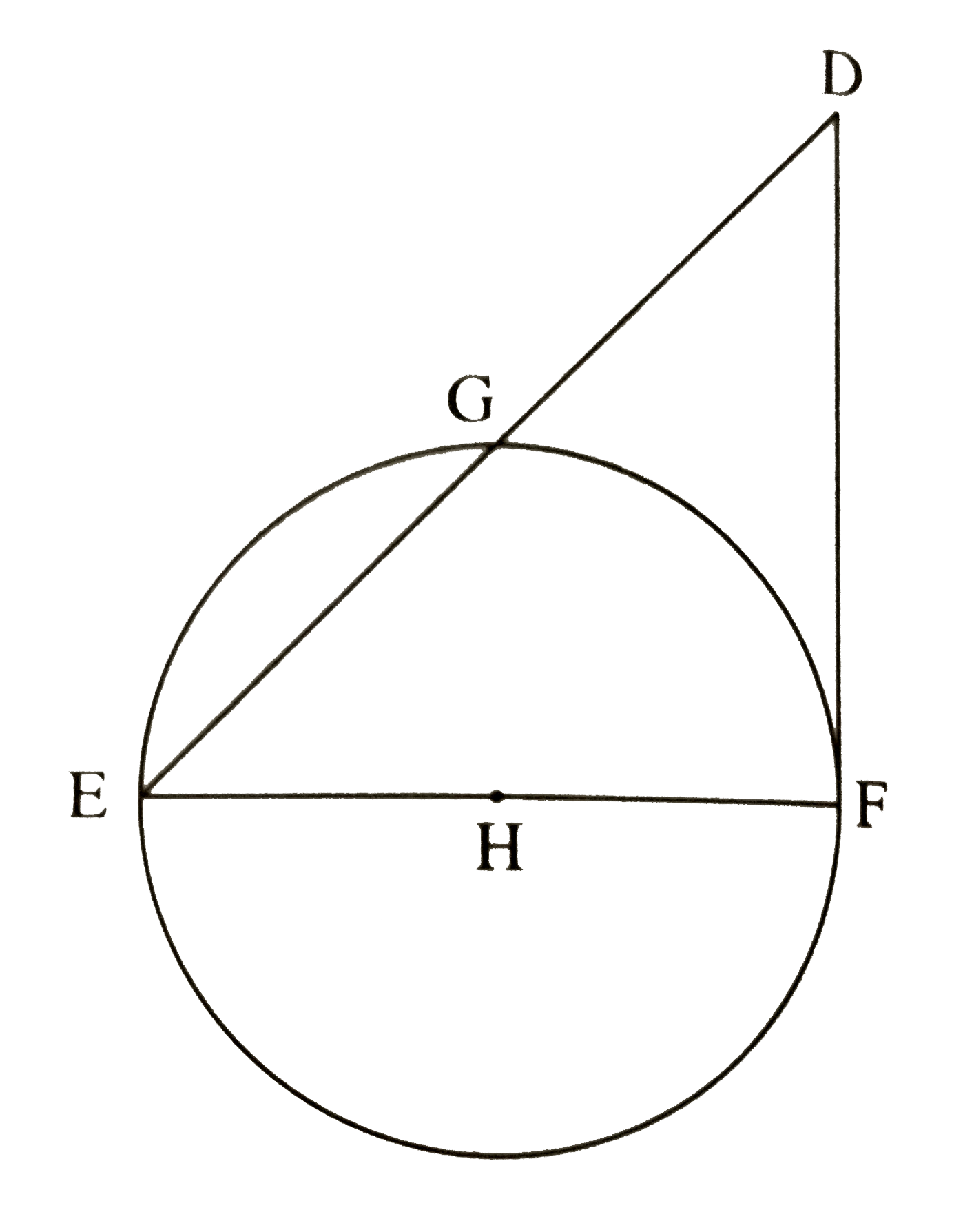
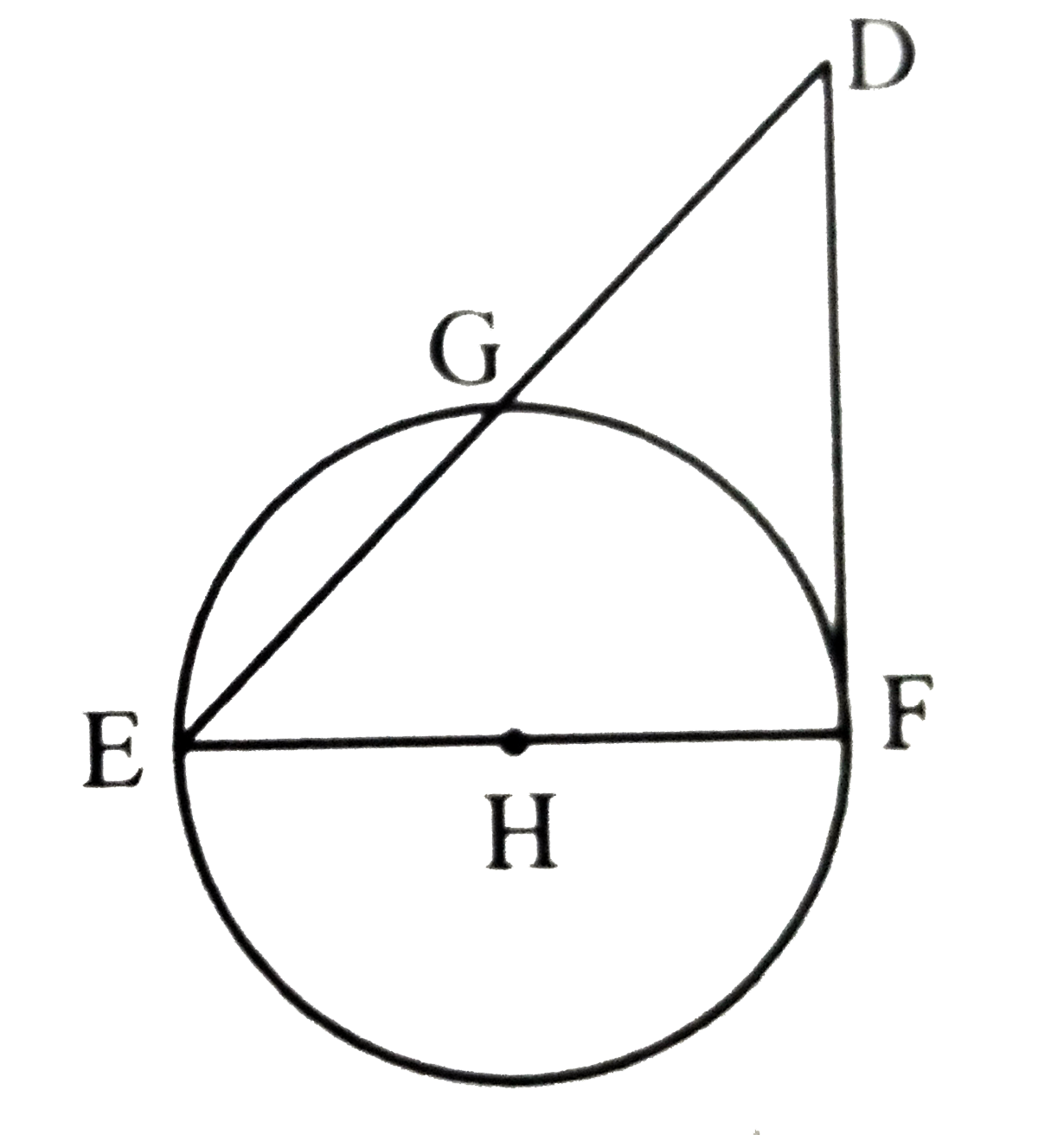
View SolutionIn the adjoining figure , seg EF is a diameter and seg DF is a tangent segment. The radius of the circle is r. Prove that, DE×GE=4r2.
View SolutionIf ∆DEF ≅ ∆BCA, write the part(s) of ∆BCA that correspond to
(i) ∠E (ii)¯¯¯¯¯¯EF (iii) ∠F (iv)¯¯¯¯¯¯DF
View Solution
