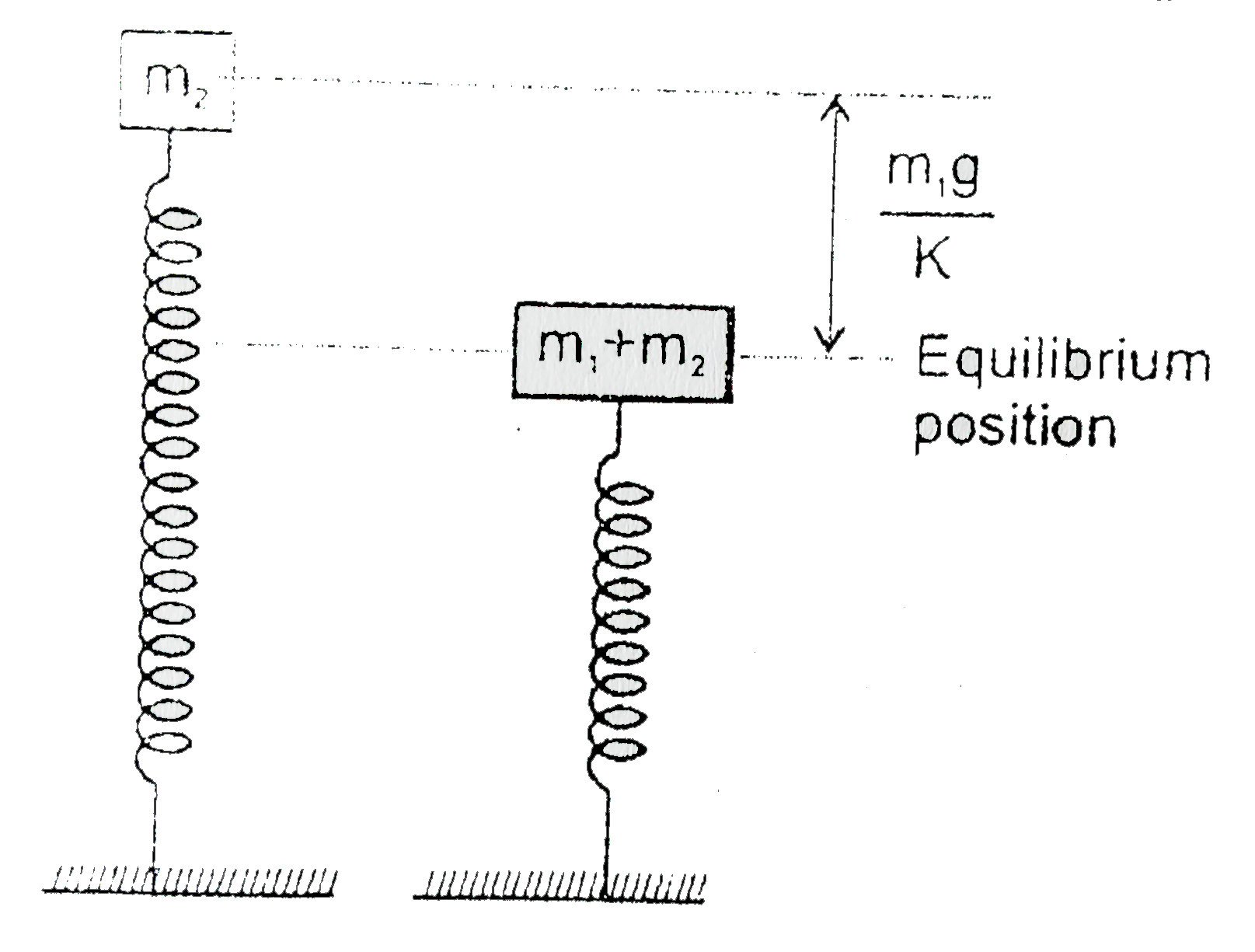
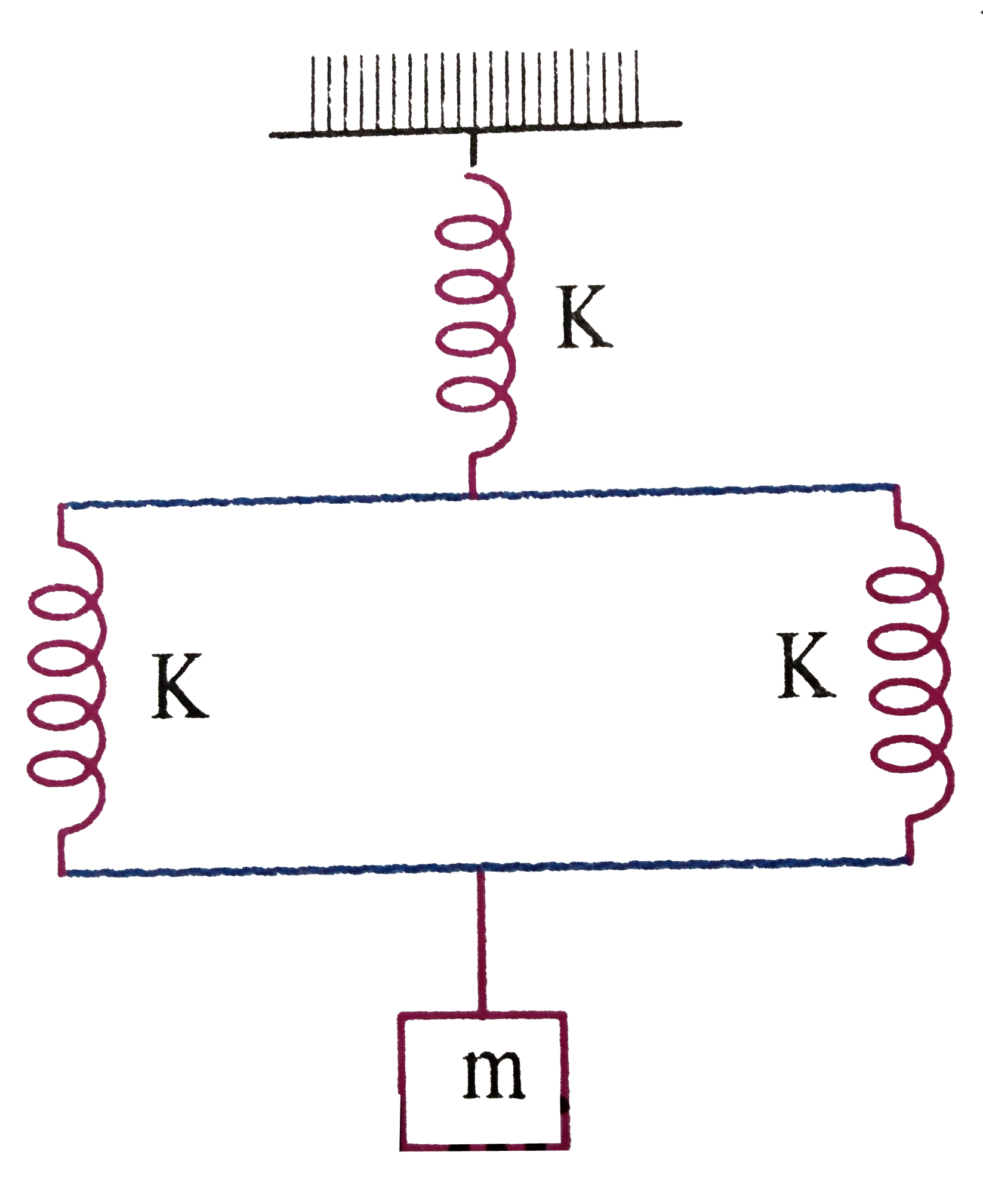
Block of mass m2 is in equilibrium as shown in figure. Anotherblock of mass m1 is kept gently on m2. Find the time period of oscillation and amplitude.
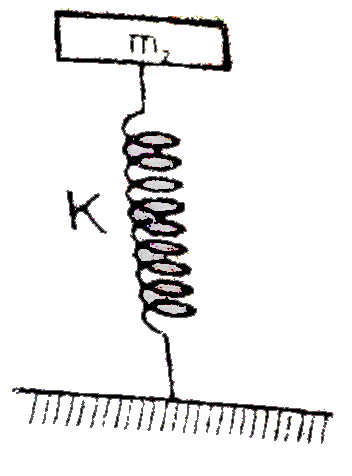
Time period T=2π√m1+m2K
At initial position since velocity is zero
it is the extreme position.
Amplitude A=m1gK
Ans. T=2π√m1+m2K Amplitude =m1gK
Topper's Solved these Questions
- BOOK - RESONANCECHAPTER - SIMPLE HARMONIC MOTION EXERCISE - Board Level Exercise24videos
SIMPLE HARMONIC MOTION
- BOOK - RESONANCECHAPTER - SIMPLE HARMONIC MOTION EXERCISE - Exercise- 1, PART - I25videos
SIMPLE HARMONIC MOTION
- BOOK - RESONANCECHAPTER - SIMPLE HARMONIC MOTION EXERCISE - Advanced Level Problems13videos
SIMPLE HARMONIC MOTION
- BOOK - RESONANCECHAPTER - SEMICONDUCTORSEXERCISE - Exercise 388videos
SEMICONDUCTORS
- BOOK - RESONANCECHAPTER - TEST PAPERSEXERCISE - FST-330videos
TEST PAPERS
Similar Questions
The system is in equilibrium and at rest. Now mass m1 is removed from m2. Find the time period and amplituded of resultant motion. Spring constant is K.
 View Solution
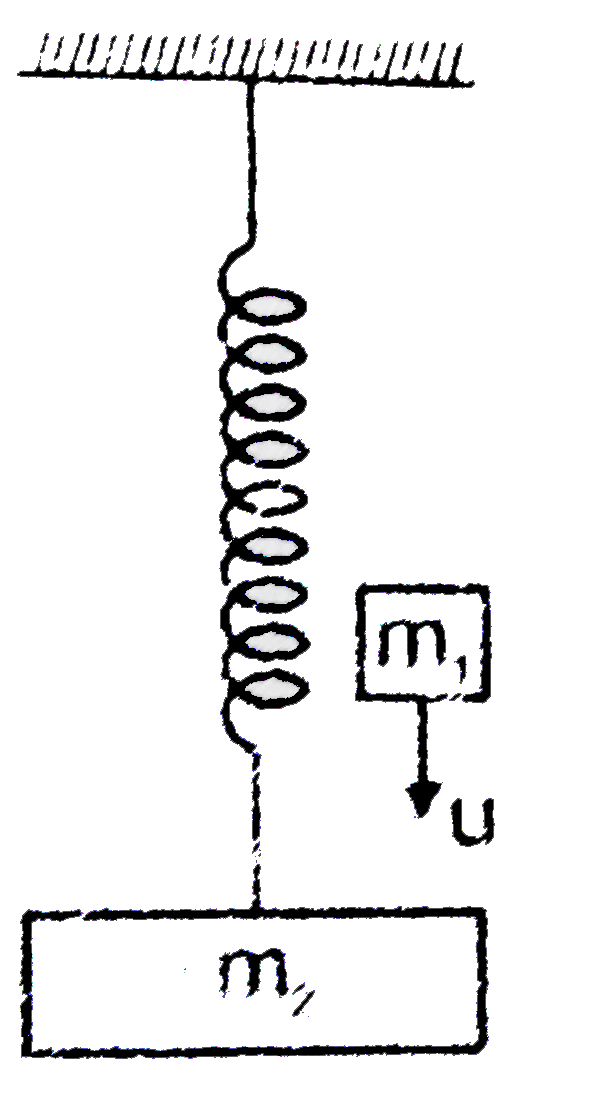
View SolutionBlock of mass m2 is in equilibrium and at rest. The mass m1 moving with velocity u vertically downwards collids with m2 and sticks to it. Find the energy of oscillation.
 View Solution
View Solution
Knowledge Check
- Question 1 - Select One
The time period of small oscillations of mass m :-
_S01_040_Q01.png) A2π√m6kB2π√11m6KC2π√6m11KD2π√mK
A2π√m6kB2π√11m6KC2π√6m11KD2π√mK - Question 2 - Select One
Spring of spring constant k is attached with a block of mass m1, as shown in figure. Another block of mass m2 is placed angainst m1, and both mass masses lie on smooth incline plane.

Find the compression in the spring when lthe system is in equilibrium.A(m1+m2)gsinθ2kB(m1+m2)gsinθkC(m1+m2)gkD2(m1+m2)gsinθk - Question 3 - Select One
In the given figure, a mass M is attached to a horizontal spring which is fixed on one side to a rigid support. The spring constant of the spring is k. The mass oscillates on a frictionless surface with time period T and amplitude A. When the mass is in equilibrium position, as shown in the figure, another mass m is gently fixed upon it. The new amplitude of oscillation will be :
 AA√M−mMBA√MM+mCA√M+mMDA√MM−m
AA√M−mMBA√MM+mCA√M+mMDA√MM−m
Block of mass m2 is in equilibrium and at rest. The mass m1 moving with velocity u vertically downwards collides with m2 and sticks to it. Find the energy of oscillation.
View SolutionBlock A of mass m is performing SHM of amplitude a. Another block B of mas m is gently placed on A when it passes through mean position and B sticks to A. Find the time period and amplitude of new SHM.
View SolutionFind the time period of SHM of the block of mass M
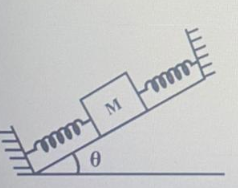 View Solution
View SolutionA body of mass m is suspended from three springs as shown in figure. If mass m is displaced slightly then time period of oscillation is
 View Solution
View SolutionTwo blocks of masses m1 and m2 are kept on a smooth horizontal table as shown in figure. Block of mass m1 (but not m2 is fastened to the spring. If now both the blocks are pushed to the left so that the spring is compressed a distance d. The amplitude of oscillatin of block of mass m1 after the system is released is
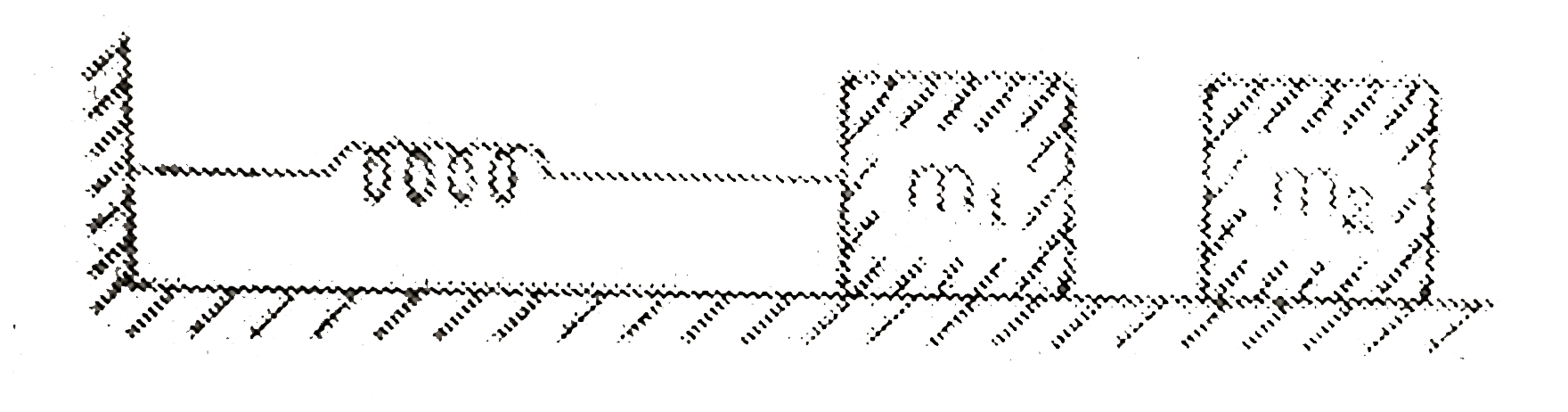 View Solution
View Solution

