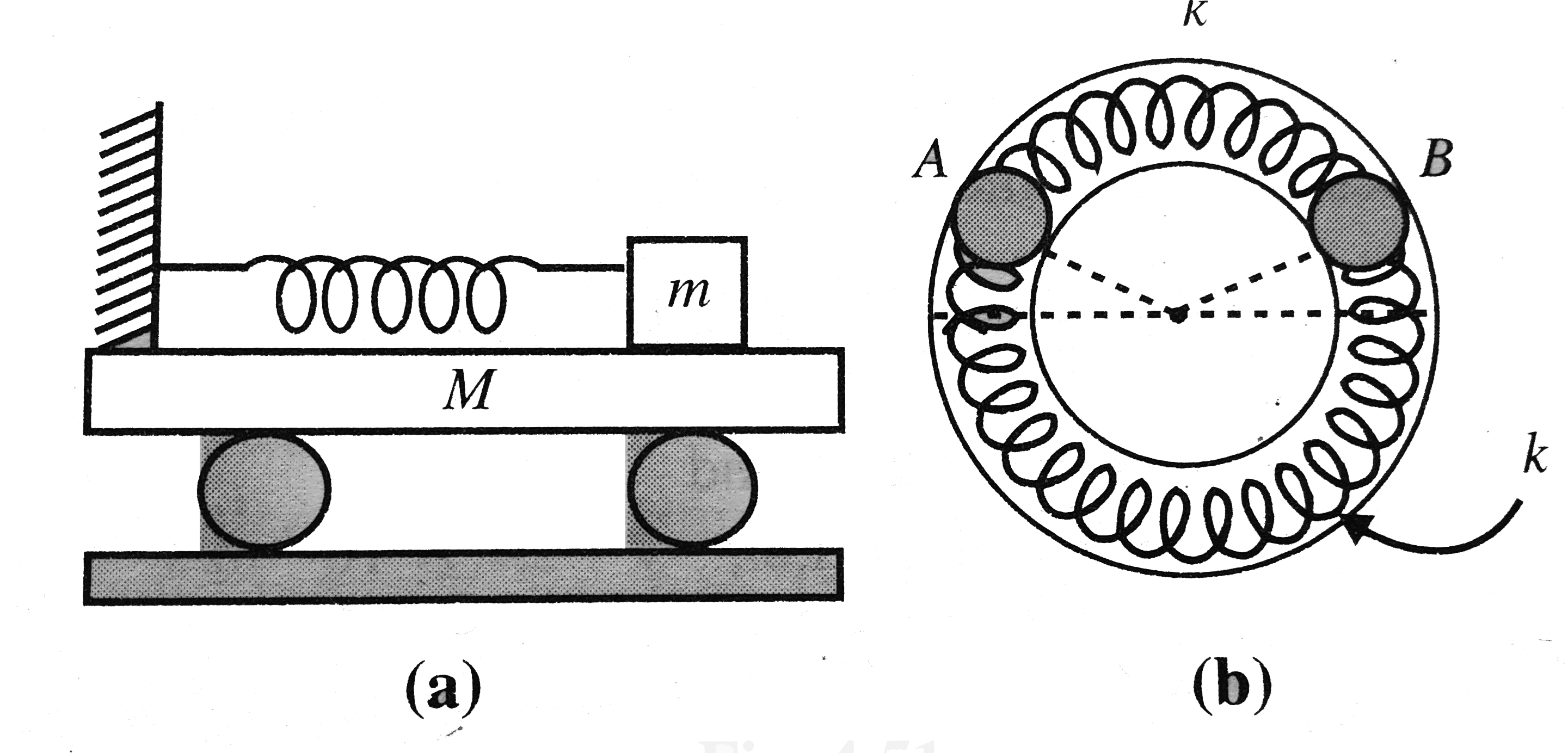
Find the time period of SHM of the block of mass M 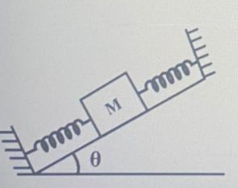
T=2π√M2K
T=2π√MK
T=2π√2MK
T=2π√M4K
The correct Answer is:A
Step by step video, text & image solution for Find the time period of SHM of the block of mass M by Physics experts to help you in doubts & scoring excellent marks in Class 12 exams.
Updated on:21/07/2023Similar Questions
Knowledge Check
Find the time period of oscillation of block of mass m. Spring, and pulley are ideal. Spring constant is k.
 A2π√mkBπ√mkC4π√mkD2π√m2k
A2π√mkBπ√mkC4π√mkD2π√m2kA and B are two thin rubber bands, each of force constant k. Assuming that they obey Hooke's law, the time period of horizontal SHM of the mass m is given by
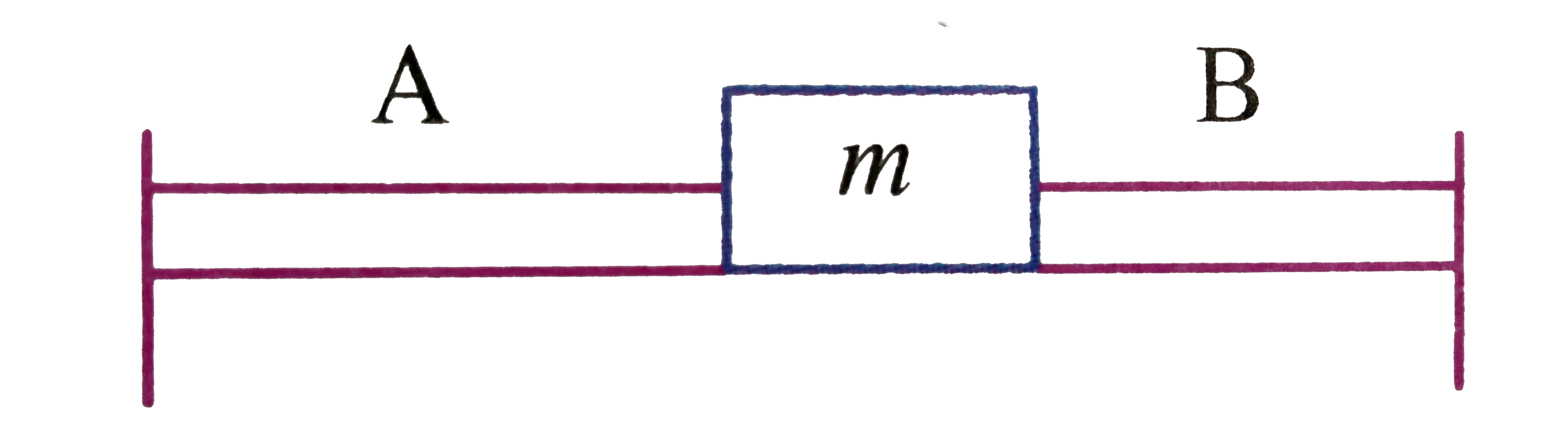 A2π√2mKBπ√mKC2π√m2KD2π√mK
A2π√2mKBπ√mKC2π√m2KD2π√mKCalculate the period of oscillations of block of mass m attached with a set of springs as shown
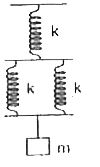 A2π√m3kB2π√3m2kC2π√2m3kD2π√3km
A2π√m3kB2π√3m2kC2π√2m3kD2π√3km
The system shown in the figure can move on a smooth surface. They are initially compressed by 6cm and then released, then choose the correct options.

(a) The system performs, SHM with time period π10s
(b) The block of mass 3kg perform SHM with amplitude 4cm
( c) The block of mass 6kg will have maximum momentum of 2.40kg−m/s
(d) The time periods of two blocks are in the ratio of 1:√2
View SolutionA block of mass 'm' is released on the top of a frictionless incline as shown in the figure. The time period of the oscillation of the block is

View SolutionInitially system is in
equilibrium . Time period of
SHM of block in vertical
direction is :

View SolutionA block of mass m is connected to another block of mass M by a spring (massless) of spring constant k. The block are kept on a smooth horizontal plane. Initially the blocks are at rest and the spring is unstretched. Then a constant force F starts acting on the block of mass M to pull it. Find the force of the block of mass M.
View SolutionA spring of force constant K is attached with a mass executes with S.H.M has a time period T. It is cut into three equal parts
If the springs are connected in parallel then the time period of the combination for the same mass is
View Solution