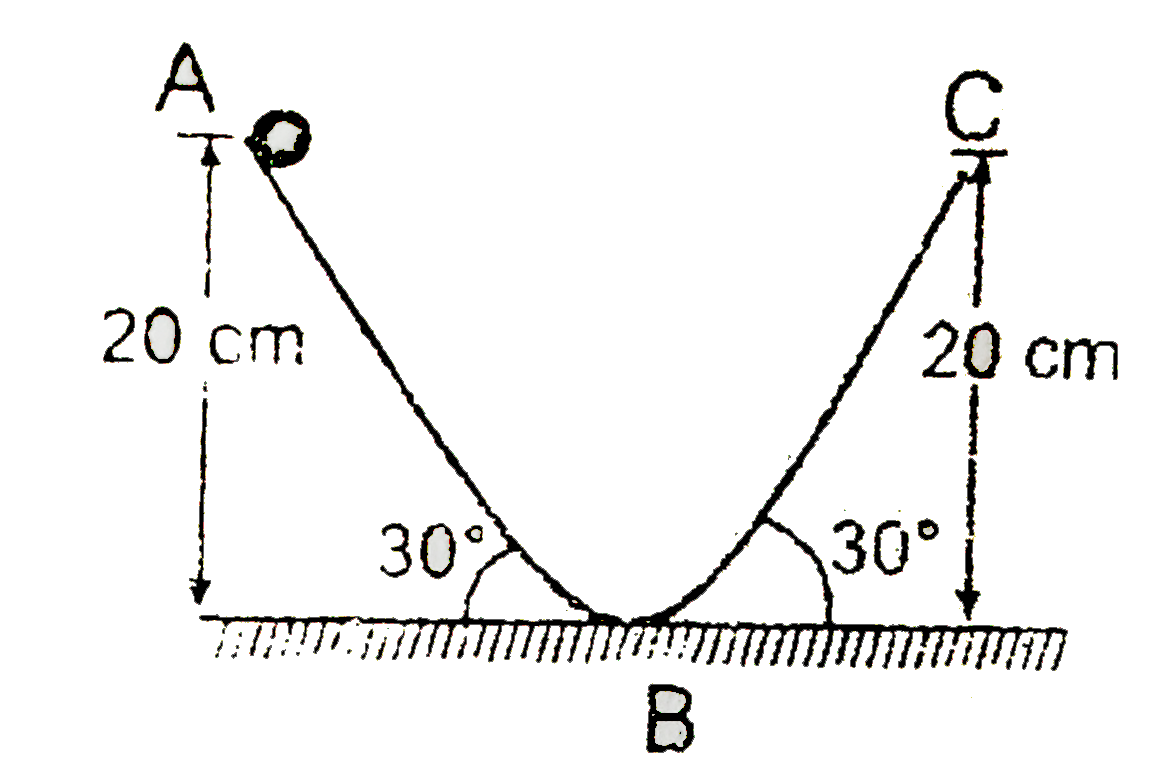
Assuming all the surfaces to be smoth, if the time period of motion of the ball is N×10−1sec then find N. Neglect the small effect of bend near the bottom. (g=10m/s2)
The correct Answer is:16
S=hsin30,a=gsin30,h=20cm,u=0
S=ut+12at2
⇒t=√2Sa=√2×(0.2×2)10×(0.5)=0.4
For BC max height reached by the particle will be same as h=20cm
(by energy conservation)
and for BA and BC,t=0.4
Total time period =0.4×4=1.6 second =16×10−1sec
∴N=16
Topper's Solved these Questions
- BOOK - RESONANCECHAPTER - SIMPLE HARMONIC MOTION EXERCISE - Exercise- 2, PART - II1videos
SIMPLE HARMONIC MOTION
- BOOK - RESONANCECHAPTER - SIMPLE HARMONIC MOTION EXERCISE - Exercise- 2, PART - III12videos
SIMPLE HARMONIC MOTION
- BOOK - RESONANCECHAPTER - SIMPLE HARMONIC MOTION EXERCISE - Exercise- 1, PART - II37videos
SIMPLE HARMONIC MOTION
- BOOK - RESONANCECHAPTER - SEMICONDUCTORSEXERCISE - Exercise 388videos
SEMICONDUCTORS
- BOOK - RESONANCECHAPTER - TEST PAPERSEXERCISE - FST-330videos
TEST PAPERS
Similar Questions
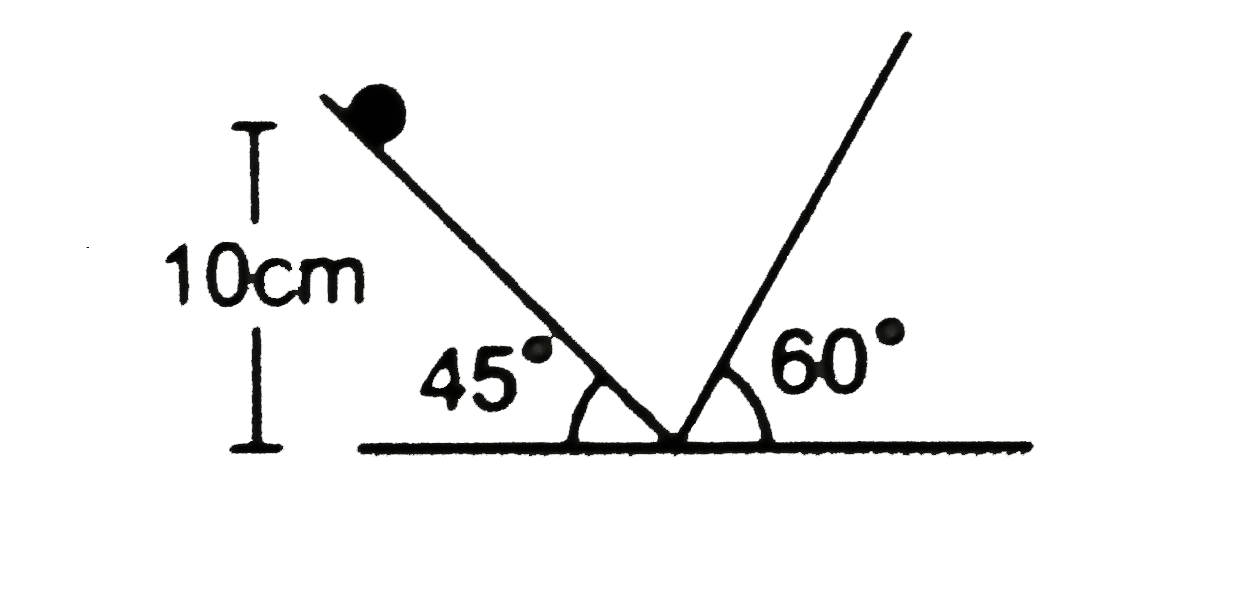
Find the time period of the motion of the particle shown in figure. Neglected small effect of the bend near the bottom.
 View Solution
View SolutionA rubber ball of mass 10 gram and volume 15cm3 is dipped in water to a depth of 10m. Assuming density of water uniform throughtout the depth, find (a) the ac celeration of the ball, and (b) the time taken by it to reach the surface if it is relased from rest. (Takeg=980cm/s2)
View Solution
Knowledge Check
- Question 1 - Select One
Form the centre of a large concave mirror of radius of curvature 3 sm , a small sperical steel ball is placed at a little distance on the mirror itself . The ball is then released to execute oscillatory motion on the mirror . The time period of motion of the ball is
(Neglect friction and take g=10ms2A2.38sB3.06sC3.44sD4.22s - Question 2 - Select One
Assuming the radius of the earth to be 6.5×106 m. What is the time period T and speed of satellite for equatorial orbit at 1.4×103 km above the surface of the earth.
A6831sand7174 ms−1B34155sand3204 ms−1C6831sand2144 ms−1D2431sand3514ms−1 - Question 3 - Select One
A pendulum suspended from the ceiling of the train has a time period of two seconds when the train is at rest, then the time period of the pendulum, if the train accelerates 10 m/s2 will be (g=10m/s2)
A2sB2√2sC2/√2sD23/4
A body of mass 10g executes SHM with amplitude 2×10−2 m and time period 2 s
Calculate the energy of the particle.View SolutionAn iron ball of mass 3 kg is released from a height of 125 m and falls freely to the ground. Assuming that the value of g is 10m/s2, calculate
(i) time taken by the ball to reach the ground
(ii) velocity of the ball on reaching the ground
(iii) the height of the ball at half the time if takes to reach the ground.View Solutionf the surface tension of water is 7×10−2 N/m then the rise of water is 7×10−2 N/m then the rise of water in a capillary tube of diameter 0.35 mm will be
View SolutionThe surface energy of a soap film formed on a frame of area 2×10−3m2is(T=40×10−3 N/m)
View SolutionA stone is thrown horizontally with a velocity of 10m/sec. Find the radius of curvature of it’s trajectory at the end of 3s after motion began. (g=10m/s2)
View Solution

