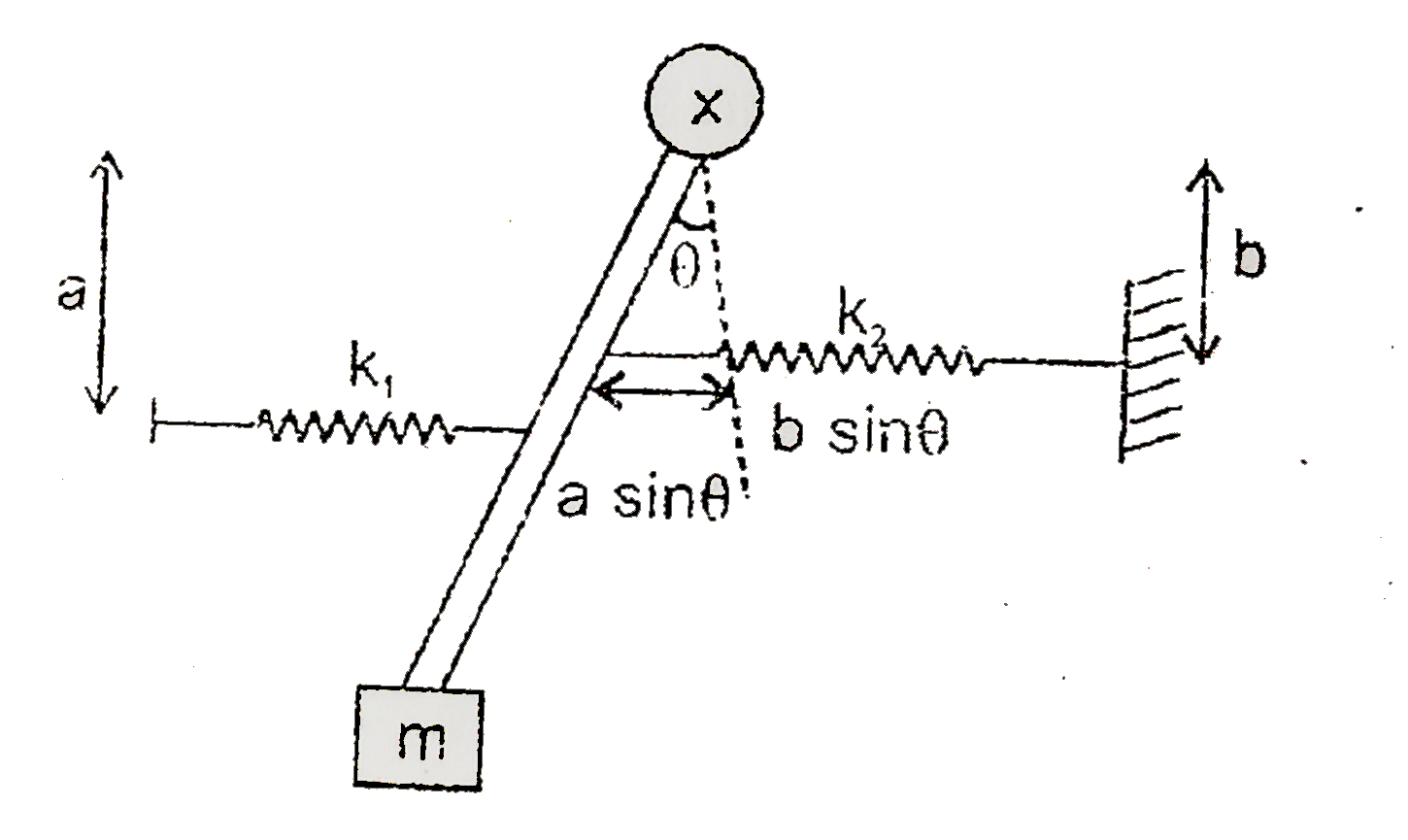
A rod of mass M and length L is hinged at its one end and carries a particle of mass m at its lower end. A spring of force constant k1 is installed at distance a from the hinge and another of force constant k2 at B distance b as shown in the figure. If the whcich arrangement rests on a smoth horizontal table top, the frequency of vibration is :
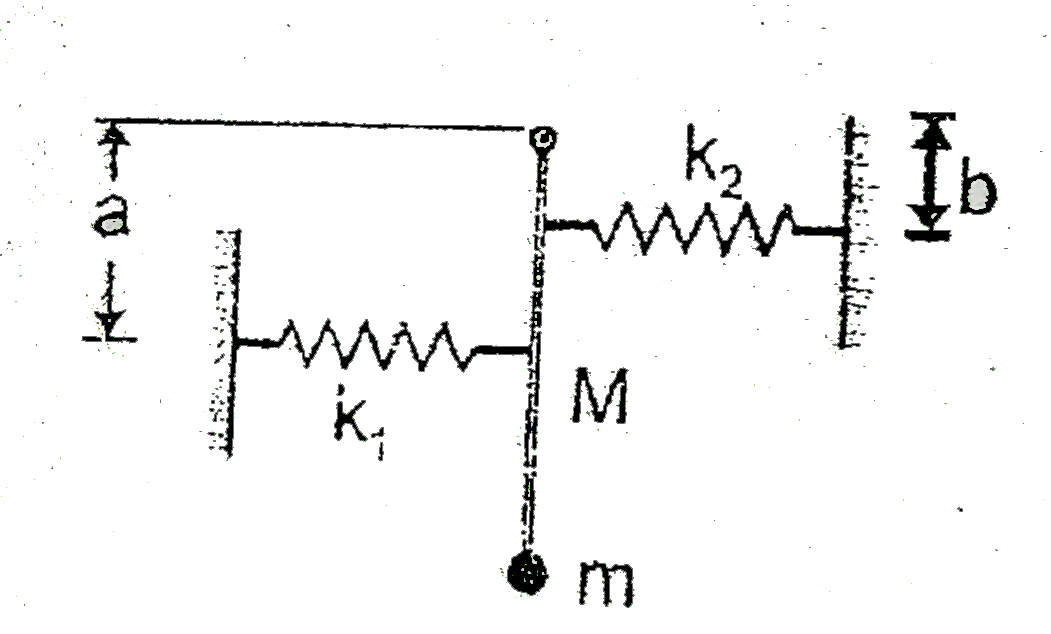
12π ⎷k1a2+k2b2L2(m+M3)
12π√k2+k1M+m
12π ⎷k2+k1a2b24M3+m
12π ⎷k1+k2b2a243m+M
The correct Answer is:A
For small angular displacement (θ)
Net torque on body =Iα
=(k1asinθ)a+(k2bsinθ)b=(mL2+ML23)α
For small θ⇒a=k1a2+k2b2mL2+ML23θ⇒ frequency =12π√k1a2+k2b2L2(m+M/3)
Topper's Solved these Questions
- BOOK - RESONANCECHAPTER - SIMPLE HARMONIC MOTION EXERCISE - Exercise- 2, PART - II1videos
SIMPLE HARMONIC MOTION
- BOOK - RESONANCECHAPTER - SIMPLE HARMONIC MOTION EXERCISE - Exercise- 2, PART - III12videos
SIMPLE HARMONIC MOTION
- BOOK - RESONANCECHAPTER - SIMPLE HARMONIC MOTION EXERCISE - Exercise- 1, PART - II37videos
SIMPLE HARMONIC MOTION
- BOOK - RESONANCECHAPTER - SEMICONDUCTORSEXERCISE - Exercise 388videos
SEMICONDUCTORS
- BOOK - RESONANCECHAPTER - TEST PAPERSEXERCISE - FST-330videos
TEST PAPERS
Similar Questions
A rod of mass M and length K is hinged at its one end n carris a block f mass m at its other end. A spring of force constant k1 is installed at distance a form the hinge and another of force constant k2 at a distance b as shown in the figure. If the whole arrangement rests on a smoth horizontal table top. Find the frequency of vibrations.
_E01_120_Q01.png) View Solution
View SolutionA uniform rod of mass 2m and length L is hinged at one end and carries a particle of mass m at the other end.Two springs each of force constant k are installed at distances as shown.The whole arrangement rests on a smooth horizontal surface.The frequency of small oscillations will be?
View Solution
Knowledge Check
- Question 1 - Select One
A thin uniform rod mass M and length L is hinged at its upper end. And released from rest from a horizontal position. The tenstion at a point located at a distance L/3 from the hinge point, when the rod become vertical will
A22Mg/27B11Mg/13C6Mg/11D2Mg - Question 2 - Select One
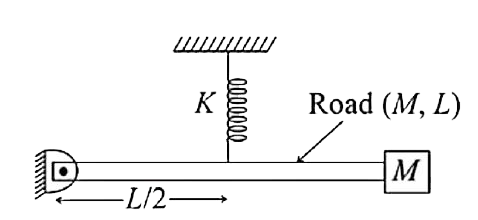
A rod of mass 'M' and length'
L' is hinged about one end and a
particle of mass 'M' is
attached to its other end If it is
kept horizontal with the help of
a spring of spring constant 'K'
as shown in fig. find the
extension in spring :-
 A3MgKBMgKC2MgKD4MgK
A3MgKBMgKC2MgKD4MgK - Question 3 - Select One
A rod of mass m and length l is hinged at 'its' end and released from rest in position shown. Find the force exerted by the hinge when the rod becomes horizontal
 Amg4B3mg2cosθCmg4√9cos2θ+14Dmg2√9cos2θ+14
Amg4B3mg2cosθCmg4√9cos2θ+14Dmg2√9cos2θ+14
Find the frequency of oscillations of the system in the figure. The bar is rigid and light.
[Hint: A spring of force constant k1 at a distance a is equivalent to a spring of force constant k1(ab)o2 at a distance b)
 View Solution
View SolutionA uniform rod of mass M and length L is hinged at its end. The rod is released from its vertical position by slightly pushing it. What is the reaction at the hinge when the rod becomes horizontal, again vertical.
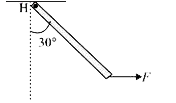
View SolutionA rod of mass m and length L is hinged at its top end. If the rod is in equilibrium making an angle of 30∘ with the vertical when a horizontal force F is applied as shown in figure, then the value of F is:
 View Solution
View SolutionTwo springs of force constant k and 2k are connected to a mass shown in figure the frequency of oscillation of the mass is
 View Solution
View SolutionTwo springs of force constant k and 2k are connected to a mass shown in figure the frequency of oscillation of the mass is
 View Solution
View Solution

