Find velocity of wave is string A &B.
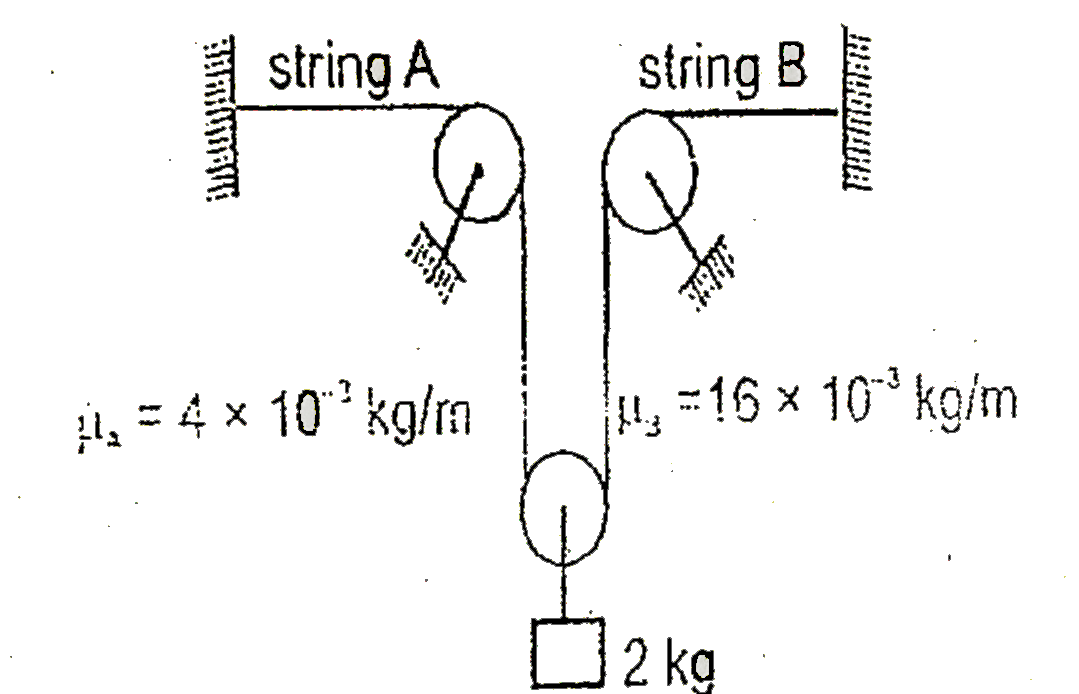
The correct Answer is:50m/sec,25m/sec
V1=√104×10−3
=50m/sec
V2=√1016×10−3
=√10416=1004=25m/sec.
Topper's Solved these Questions
Similar Questions
A transverse wave travelling in a string produce maximum transverse velocity of 3m/s and maximum transverse acceleration 90m/s2 in a particle. If the velocity of wave in the string is 20m/s. Datermine the equation of the wave ?
View SolutionA wave is propagating on a long stretched string along its length taken as positive x-axis the wave equation is given by
y=y0e−(tT−xλ)2,wherey0=2mm
T = 1 . 0 sec and λ=6cm find .
Plot the shape of the string at t = 6 sec.
View Solution
Knowledge Check
The velocity of wave in a stretched string is proportional to
A√TBTC1/TD1/√TThe velocity of waves in a string fixed at both ends is 3 m/s. The string forms standing waves with nodes 6 cm apart. The frequency of vibration of the string is
A25 HzB50 HzC15 HzD10 HzThe velocity of waves in a string fixed at both ends is 2 m / s . The string forms standing waves with nodes 5.0 cm apart. The frequency of vibration of the string in Hz is
A40B30C20D10
If T is the tension in the sting μ is the linear density of the string,then the velocity of transverse wave in the string
View SolutionA wave is propagating along the length of a string taken as positive x-axis. The wave equation is given by
y=Ae(−tt−xA)2
where A=5mm, T=1.0 s and λ=8.0cm
(a) Find the velocity of the wave. (b) find the function f(t) represent the displacement of particle at x=0. (c ) Plot the function g(x) representing the shape of the string at t=0 (d) Plot the function g(x) of the string at t=0 and t=5 s
View SolutionStationary waves are produced in a stretched string of length 120 c. if the string vibrats with 6 segment and if the frquency of vibration of the string is 20 Hz. Then the velocity of waves on the string is
View SolutionA string fixed at both the ends forms standing waves with node separation of 5 cm. If the velocity of waves travelling in the string is 4 m/s, then the frequency of vibration of the string will be
View SolutionFind velocity of ring B (VB) at the instant shown. The string is taut and inextensible:
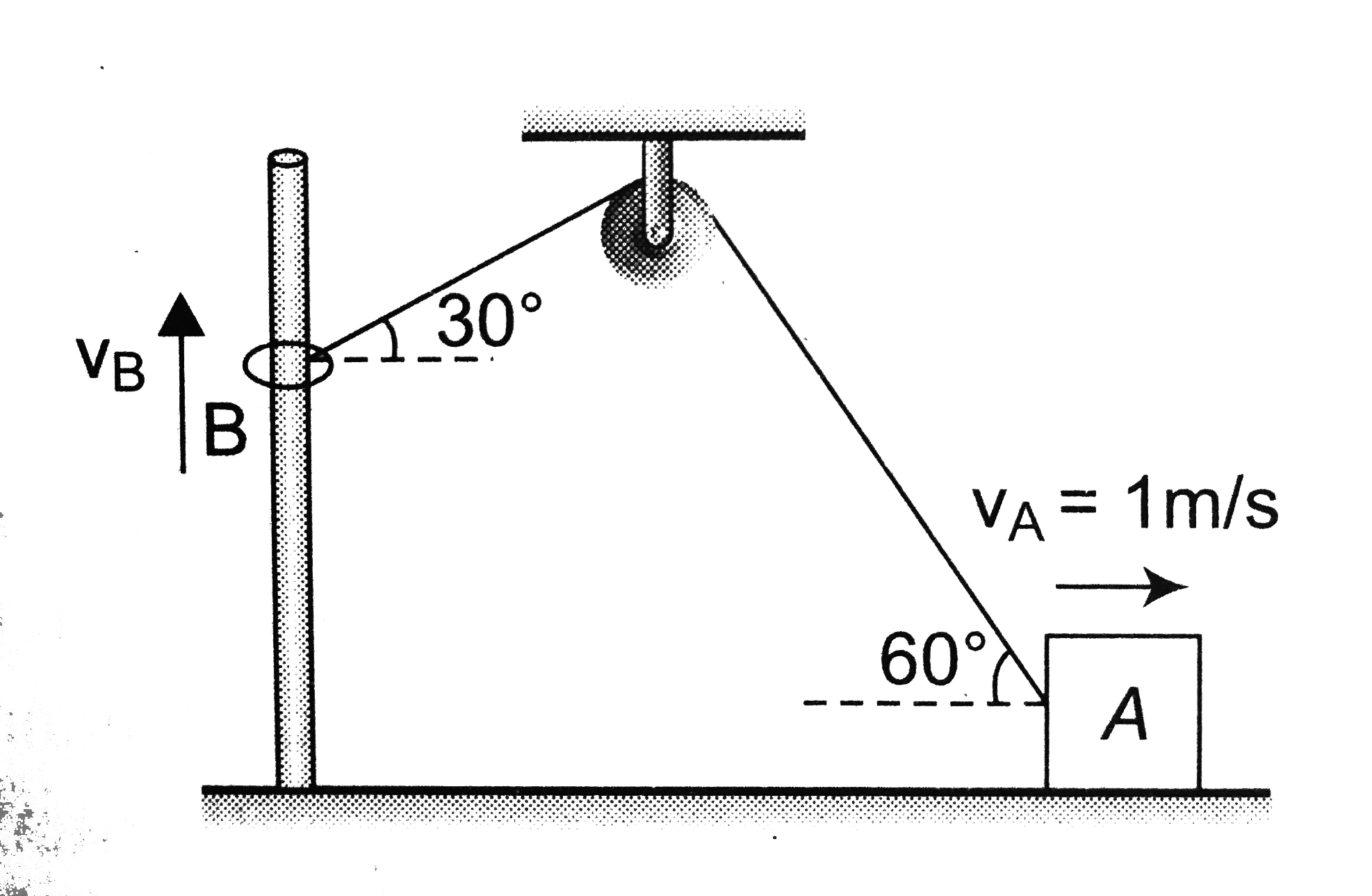
View Solution
