Two parallel beams of light P and Q (separation d) containing radiation of wavelengths 4000A and 5000A (which are mutually coherent in each wavelength separately) are incident normally on a prism as shown in fig. The refractive index of the prism as a function of wavelength is given by the relation. μ(λ)=1.20+bλ2 Where λ is in A and b is positive constant. The value of b is such that the condition wave length and is not satisfied for the other.
(a) Find the value of b.
(b) find the deviation of the beams transmitted through the face AC. (c) A convergent lens is used to bring these transmitted beams into focus. If the intensities of transmission form the face AC, are 41 and I respectively, find the resultant intensity at the focus.

The correct Answer is:9 I
Values of μ,α etc. are given because there 2 more parts asked in actual J∃ paper based on value of 'b' and δ. But for finding the intensity, we don't need any of this.
The paths of 2 rays is as show. Clearly the path difference between them is.
PQ−μRS
=(PS)cos(90−r)−μ.dtanθ
=(PS)sinr−μdtanθ.
Now , by snells. lwa.
μsinθ=1.sinr.andPS=dcosθ
we get path difference =dμsinθcosθ−μdtanθ=0.
Hence the intensity is maximum at 9I.

Topper's Solved these Questions
Similar Questions
_E01_106_Q01.png)
Two parallel beams of light P and Q (separation d) containing radiations of wavelengts 4000Å and 5000 Å (which are mutually coherent in each wavelength separately) are incident normally on a prism as shown in figure the refractive index of the prism as a function of wavelength is given by the relation μ(λ)=1.20+bλ2 where λ is in Å and b is a positive constant. The value of b is such that the condition for total reflection at the face AC is just satisfied for one wavelength and is not satisfied for the other. A convergent lens is used to bring these transmitted beams into focus. If the intensities of the upper and the lower beams immediately after transmission from the face AC, are 4I and I respectively, find the resultant intensity at the focus.
View SolutionShow that the do Broglie wavelength λ of an electron of energy E is given by the relation λ==h√2mE
View Solution
Knowledge Check
The energy of a photon of wavelength λ is given by
AhλBchλCλ/hcDhc/λThe refractive index of a medium is given by μ=A+Bλ2 where A and B are constants and λ is the wavelength of light.
Then the dimensions of B are the same as that ofAWavelengthBAreaCVolumeDVelocityWhen light of wavelength λ on an equilateral prism, kept on its minimum deviation position, it is found that the angle of deviation equals the angle the angle of the prism itself. The refractive index of the material of the prism for the wavelength λ is
A√3B√3/2C2D√2
According to Cauchy's formula, the refractive index μ of a material is related to wavelength λ as………. .
View Solution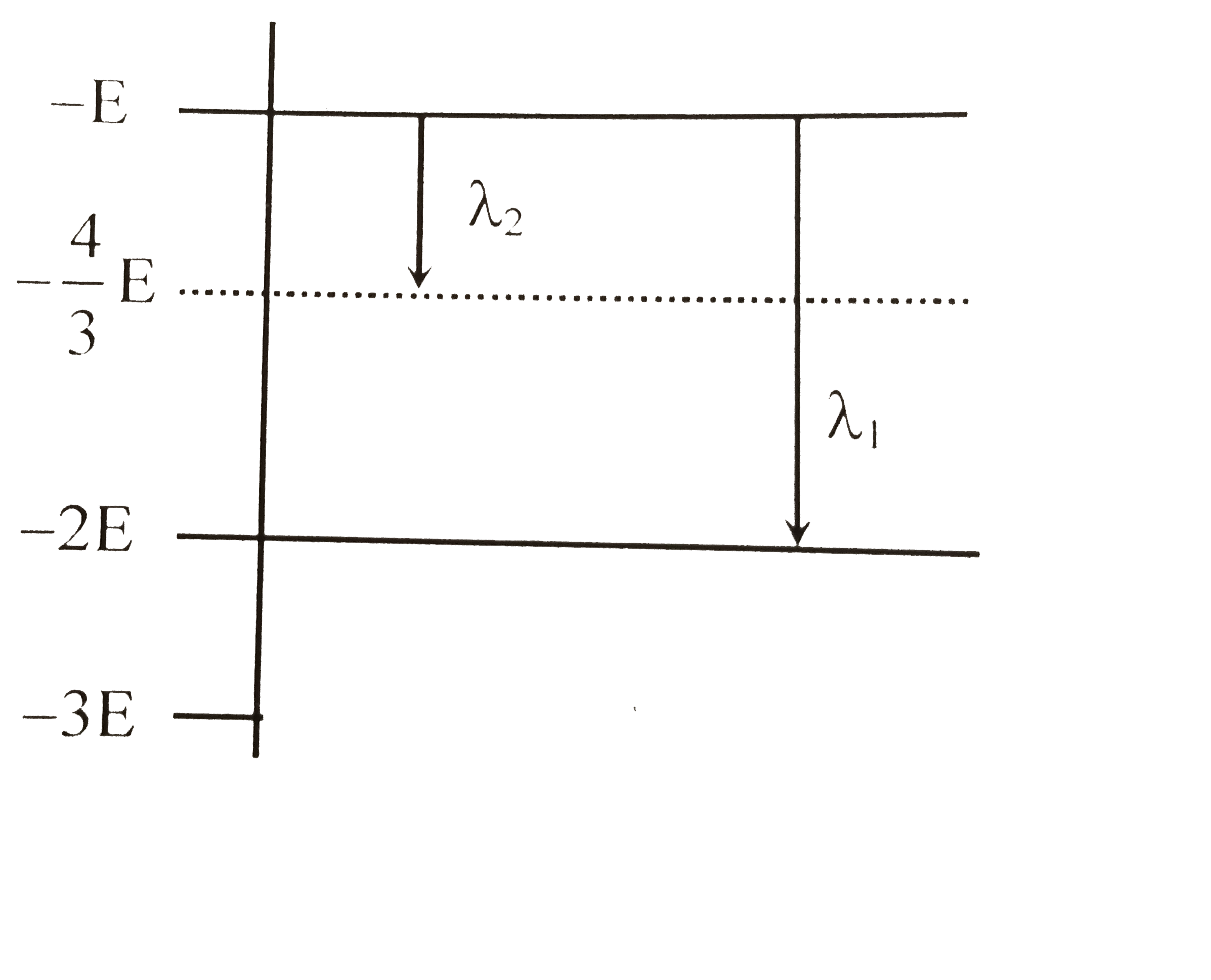
Some energy levels of a molecule are shown in the figure. The ratio of the wavelength r=λ1λ2,is given by:
View SolutionThe refractive index of light in glass varies with its wavelength according to equation
μ(λ)=a+bλ2 where a and b are positive constants.
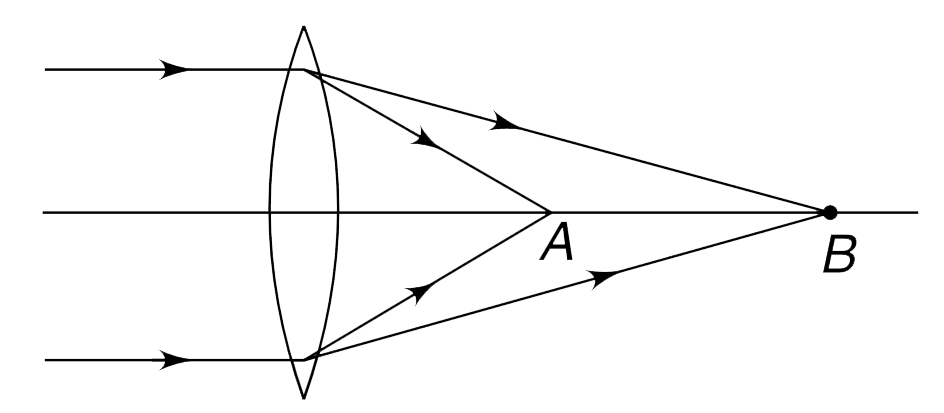
A nearly monochromatic parallel beam of light is incident on a thin convex lens as shown. The wavelength of incident light is λ0±Δλ where Δλ<<λ0. The light gets focused on the principal axis of the lens over a region AB. If the focal length of the lens for a light of wavelength λ0 is f0, find the spread AB.
View SolutionFind the thickness of a plate which will produce a change in optical path equal to half the wavelength λ of the light passing through it normally. The refractive index of the plate is μ.
View SolutionThe angles of incidence and refraction of a monochromatic ray of light of wavelength λ at an air-glass interface are i and r, respectively. A parallel beam of light with a small spread δλ in wavelength about a mean wavelength λ is refracted at the same air-glass interface. The refractive index μ of glass depends on the wavelength λ as μ(λ)=a+b/λ2 where a and b are constants. Then the angular spread in the angle of refraction of the beam is
View Solution
