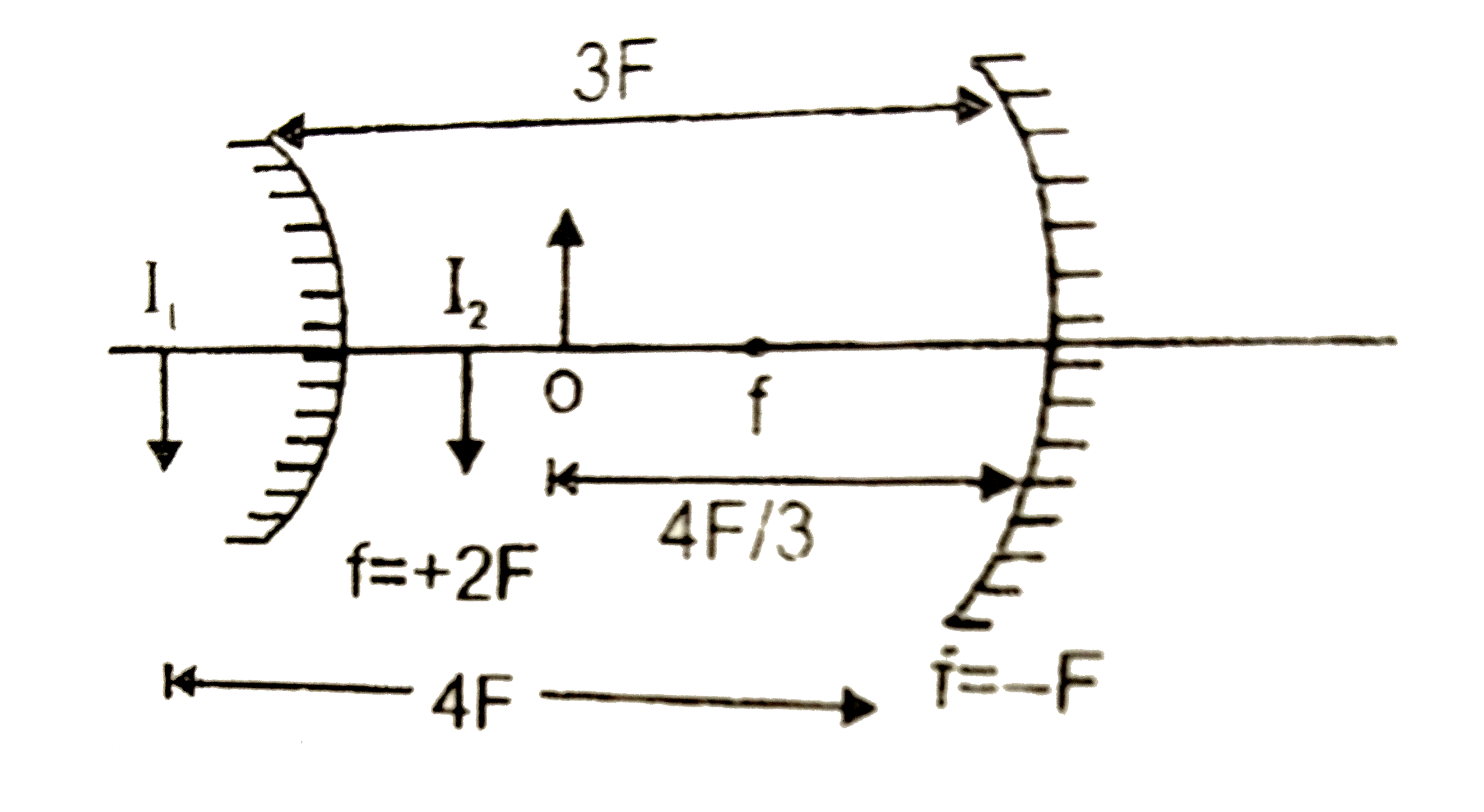
A buring candle is placed in front of a concave spherical mirror on its principal optical axis at a distance of form the pole of the mirror (here is the focal length of the mirror). The candle is arranged at right angle to the axis. The image of the candle in the concave mirror impinges upon a convex mirror of focal length . The distance between the mirrors is and their axes coincide. The image of the candle in the first mirror plays the part of a virtual object with respect to the second mirror and gives a real image arranged between the two mirrors. Find the total linear magnification (magnitude only) of the system.
The correct Answer is:6
For reflection by concave mirror.
Hence
For reflection by concave mirror,
magnification by concave mirror.
Net magnification
Topper's Solved these Questions
- GEOMATRICAL OPTICS BOOK - RESONANCECHAPTER - GEOMATRICAL OPTICS EXERCISE - Exercise-3
79 Videos
- GEOMATRICAL OPTICS BOOK - RESONANCECHAPTER - GEOMATRICAL OPTICS EXERCISE - Advance level Problems
35 Videos
- GEOMATRICAL OPTICS BOOK - RESONANCECHAPTER - GEOMATRICAL OPTICS EXERCISE - Exercise-1
142 Videos
- EXPERIMENTAL PHYSICSBOOK - RESONANCECHAPTER - EXPERIMENTAL PHYSICSEXERCISE - PART -II
10 Videos
- GRAVITATIONBOOK - RESONANCECHAPTER - GRAVITATIONEXERCISE - HIGH LEVEL PROBLEMS
16 Videos
Similar Questions
An object is placed midway between a concave mirror of focal length f and a convex mirror of focal length f. The distance between the two mirrors is 6f. Trace the ray that is first incident on the concave mirror and then the convex mirror.
View SolutionAn object is placed midway between a concave mirror of focal length f and a convex mirror of focal length f. The distance between the two mirrors is 6f. Trace the ray that is first incident on the concave mirror and then the convex mirror.
View Solution
Knowledge Check
An object is placed at a distance of 30 cm from a concave mirror and its real image is formed at a distance of 30 cm from the mirror. The focal length of the mirror is
A15 cmB45 cmC30 cmD20 cmAn object is placed at a distance u from a concave mirror and its real image is received on a screen placed at a distance of v from the mirror. If f is the focal length of the mirror, then the graph between 1/v versus 1/u is
A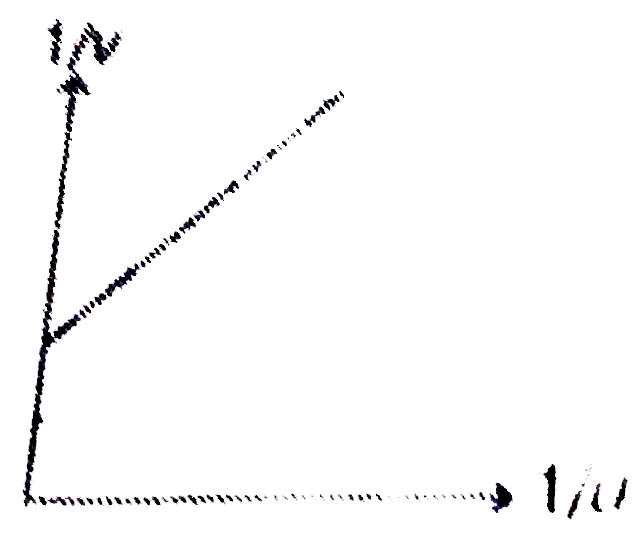 B
B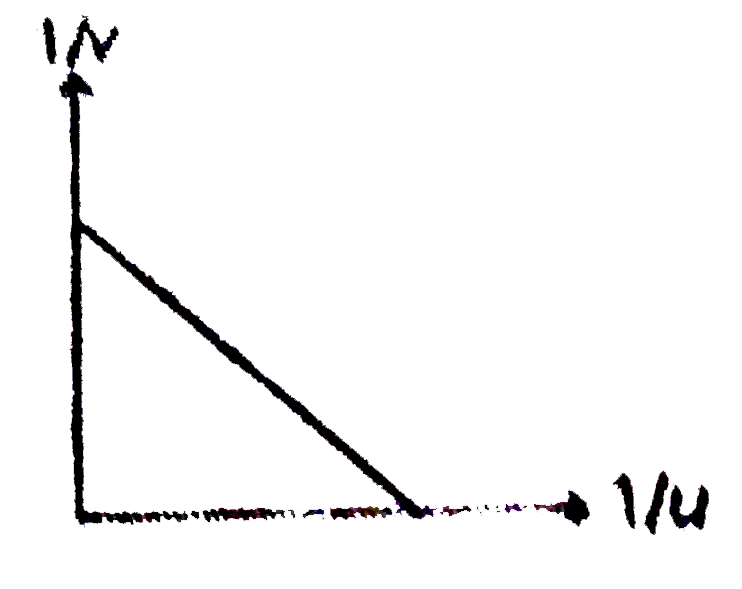 C
C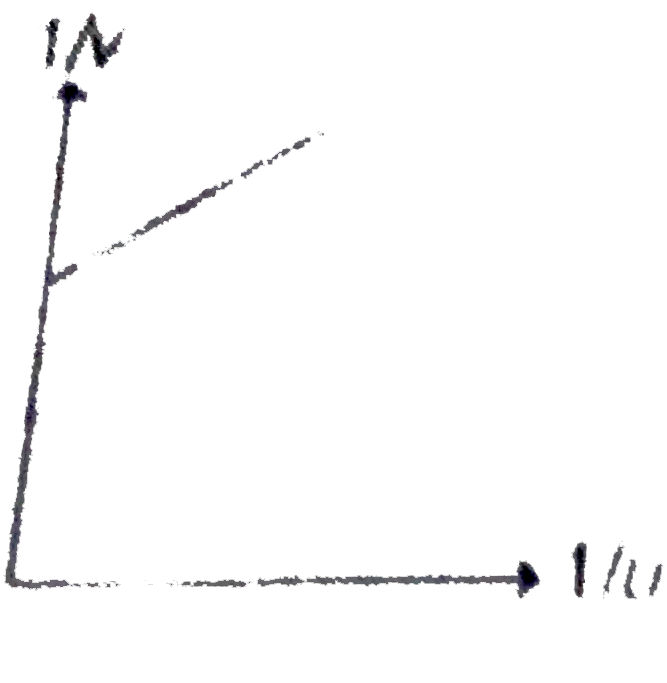 D
D
A real object is placed at a distance f from the pole of a convex mirror, infront of the convex mirror. If focal length of the mirror is f, then distance of the image from the pole of the mirror is
A2fBf2C4fDf4
An object is placed at a distance of 30 cm from a concave mirror and its real image is formed at a distance of 30 cm from the mirror. The focal length of the mirror is
View SolutionAn object is placed in front of a concave mirror at a distance of 7.5 cm from it. If the real image is formed at a distance of 30 cm from the mirror, find the focal length of the mirror. What would be the focal length if the image is virtual.
View SolutionAn object is placed in front of a concave mirror at a distance of 7.5 cm from it. If the real image is formed at a distance of 30 cm from the mirror, find the focal length of the mirror. What would be the focal length if the image is virtual.
View SolutionAn object is placed at a distance u from a concave mirror and its real image is received on a screen placed at a distance of v from the mirror. If f is the focal length of the mirror, then the graph between 1/v versus 1/u is
View SolutionAn object is placed at a distance f in the front of a convex mirror. If focal length of the mirror is f, then distance of image from pole of the mirror is
View Solution
