A hemispherical portion of the surface of a solid glass sphere (mu = 1.5) of radius r is silvered to make the inner side reflecting. An object is placed on the axis of the hemisphere at a distance 3r from the centre of the sphere. The light from the object is refracted at the unsilvered part, then reflected from the silvered part and again refracted at the unsilvered part. Locate the final image formed.
The correct Answer is:0
Let the object be placed at A
Then for refraction at the unsilvered part u=−2r,R=r .
thareforeμ2v−μ1u=μ2−μ1R
=3/2v−1(−2r)=32−1r⇒v=∞
so, image formed at infinity will act as an object for the silvered part and hence the image will be formed at the foucs of thhe concave mirror i.e., at r2 distance left ward from D
Again for refraction at the unsilvered surface u=(r+r2)=3r2
∴1v−323r2=1−32r or v=2r. Hence the final formed at D
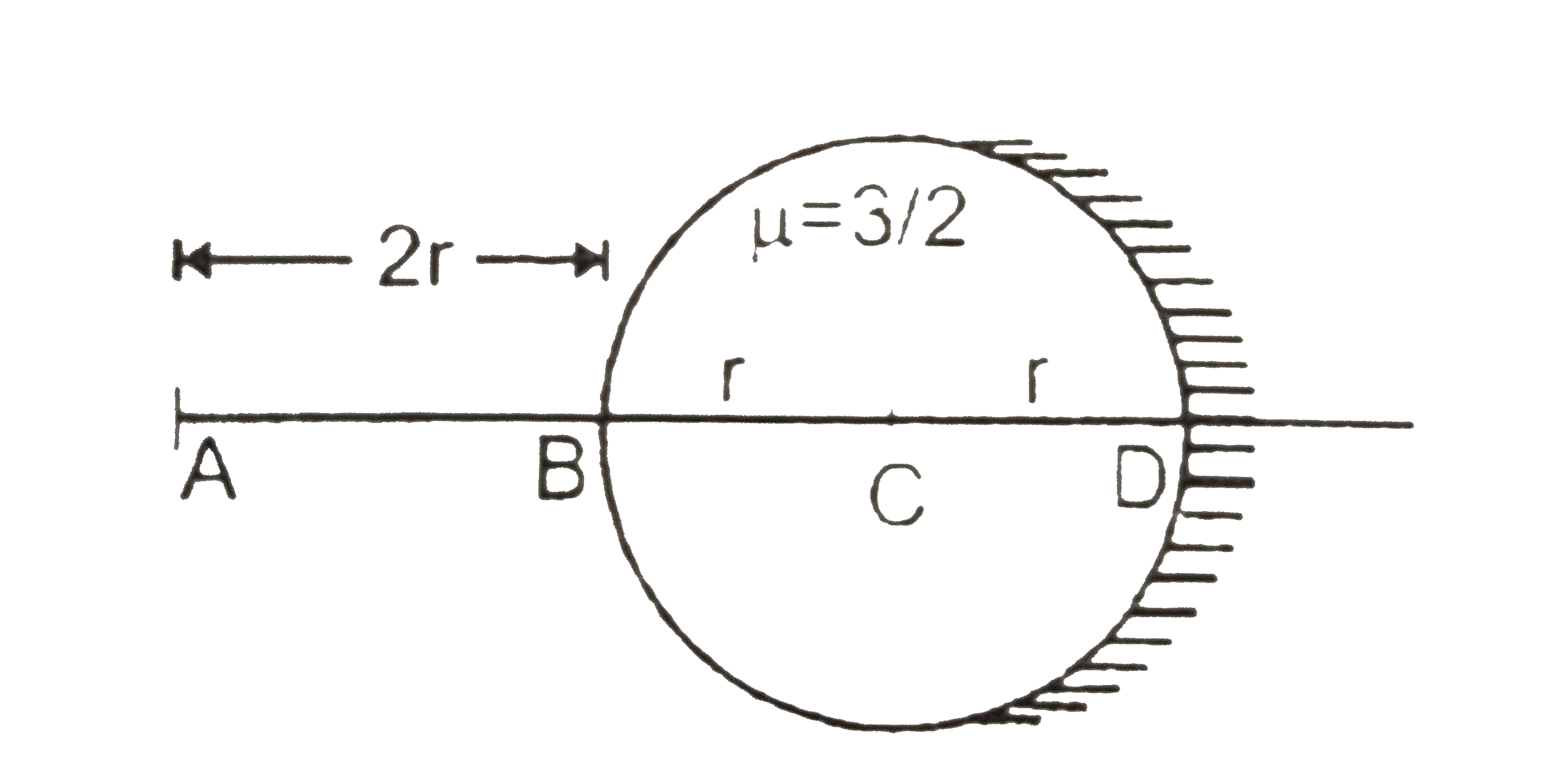
Topper's Solved these Questions
- GEOMATRICAL OPTICS BOOK - RESONANCECHAPTER - GEOMATRICAL OPTICS EXERCISE - Exercise-3
79 Videos
- GEOMATRICAL OPTICS BOOK - RESONANCECHAPTER - GEOMATRICAL OPTICS EXERCISE - Advance level Problems
35 Videos
- GEOMATRICAL OPTICS BOOK - RESONANCECHAPTER - GEOMATRICAL OPTICS EXERCISE - Exercise-1
142 Videos
- EXPERIMENTAL PHYSICSBOOK - RESONANCECHAPTER - EXPERIMENTAL PHYSICSEXERCISE - PART -II
10 Videos
- GRAVITATIONBOOK - RESONANCECHAPTER - GRAVITATIONEXERCISE - HIGH LEVEL PROBLEMS
16 Videos
Similar Questions
A solid glass sphere with radius R and an index of refraction 1.5 is silvered over one hemisphere. A small object is located on the axis of the sphere at a distance 2R to the left of the vertex of the unsilvered hemisphere. Find the position of final image after all refractions and reflection have taken place.
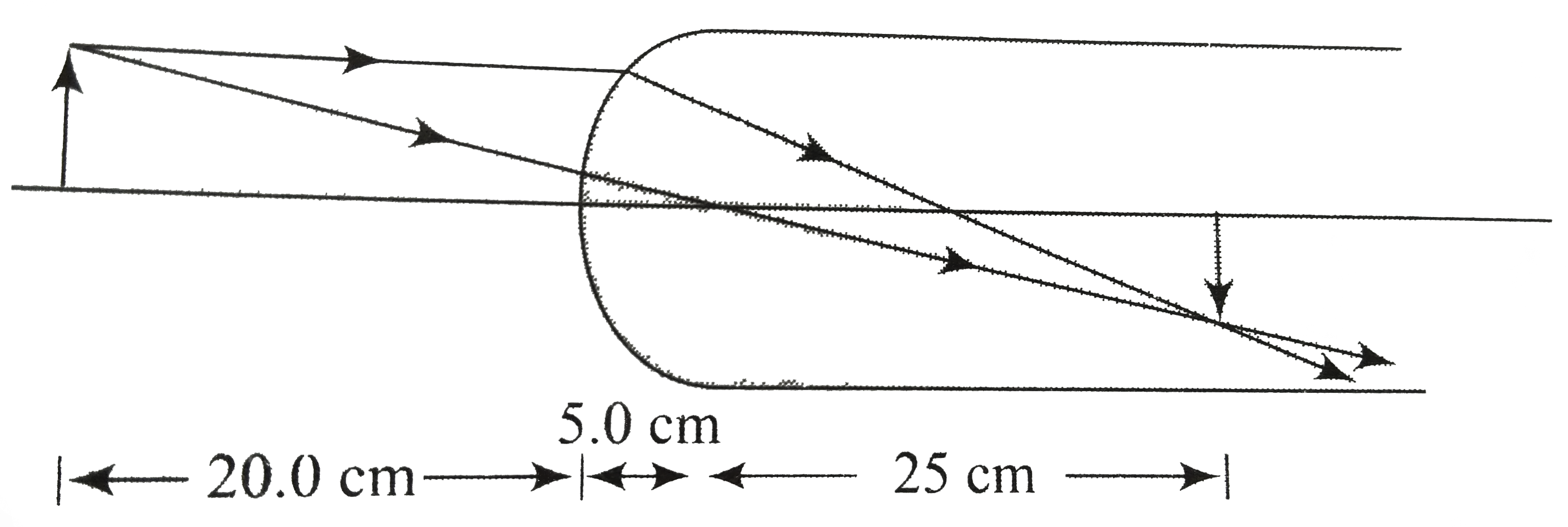
View SolutionOne end of a horizontal cylindrical glass rod (μ=1.5) of radius 0.5cm is rounded in the shape of a hemisphere. An object 0.5mm high is placed perpendicular to the axis of the rod at a distance of 20.0cm from the rounded edge. Locate the image of the object and find its height
View Solution
Knowledge Check
The distance of the centre of mass of a hemispherical shell of radius R from its centre is
AR2BR3C2R2D2R3An object is placed in front of a sphere of radius R at a distance x from the first surface. The value of x for which the light after refraction from the first surface becomes parallel to the axis is
ARμ−1BRμ+1C2R1+μDRμμ+1There is a small air bubble at the centre of a solid glass sphere of radius 'r' and refractive index μ. What wil be the apparent distance of the bubble from the centre of the sphere, when viewed from outside?
ArBrμCr(1−1μ)DZero
A glass sphere (μ=1.5) of radius 8 cm is placed in sunlight. Where is the image of the sun formed by the light passing through the sphere after refraction by second surface of sphere ?
View SolutionOne end of a cylindrical glass rod (mu = 1.5) of radius 1.0 cm is rounded in the shape of a hemisphere. The rod is immersed in water (mu= 4/3) and an object is placed in the water along the axis of the rod at a distance of 8.0 cm from the rounded edge. Locate the image of the object.
View SolutionThe radius of gyration of a solid sphere of radius r about a certain axis is r. The distance of this axis from the centre of the sphere is
View SolutionA mark is made on the surface of a glass sphere of diameter 10 cm and refractive index 1.5. It is viewed through the glass from a portion directly opposite. The distance of the image of the mark from the centre of the sphere will be
View SolutionA point object is placed at the centre of a glass sphere of radius 6 cm and refractive index 1.5. The distance of the virtual image from the surface of the glass is
View Solution
