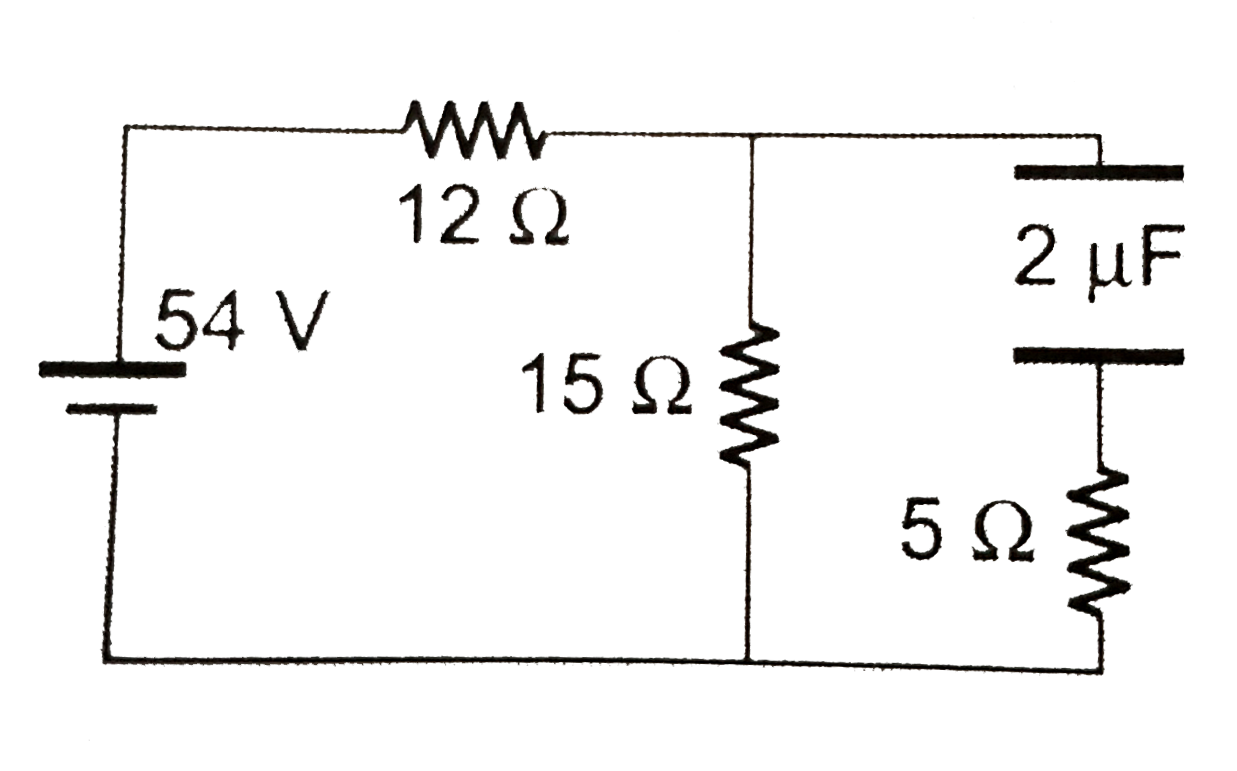Find at centre in the following cases:


Text Solution
The correct Answer is:(i), (ii) , (iii) , (iv)
(v) , (vi)
(vii) , (viii)
(i)
(ii)
(iii)
(iv)
(v)
(vi)
(vii)
(viii)
|
Topper's Solved these Questions
- ELECTRODYNAMICSBOOK - RESONANCECHAPTER - ELECTRODYNAMICSEXERCISE - Exercise-1 PART-1
81 Videos
- ELECTRODYNAMICSBOOK - RESONANCECHAPTER - ELECTRODYNAMICSEXERCISE - Exercise-1 PART-2
54 Videos
- ELECTRODYNAMICSBOOK - RESONANCECHAPTER - ELECTRODYNAMICSEXERCISE - Advanced level problems
31 Videos
- ELECTRO MAGNETIC WAVESBOOK - RESONANCECHAPTER - ELECTRO MAGNETIC WAVESEXERCISE - Exercise 3
27 Videos
- ELECTROMAGNETIC INDUCTIONBOOK - RESONANCECHAPTER - ELECTROMAGNETIC INDUCTIONEXERCISE - A.l.P
19 Videos
Similar Questions
Knowledge Check
there is a rod AB of uniform cross section and its centre is C. In which of the following case(s) centre of mass of the rod may lie at C.
ADensity of the material of rod increases continuously from A to B.BDensity of the material of rod increases continuously from B to A.CDensity of the material of rod increases from A to C and then decreases from C to BDDensity of the material of rod decreases from A to C and then increases from C to B.
Find current i in the circuit in the following cases.
(a)
(b)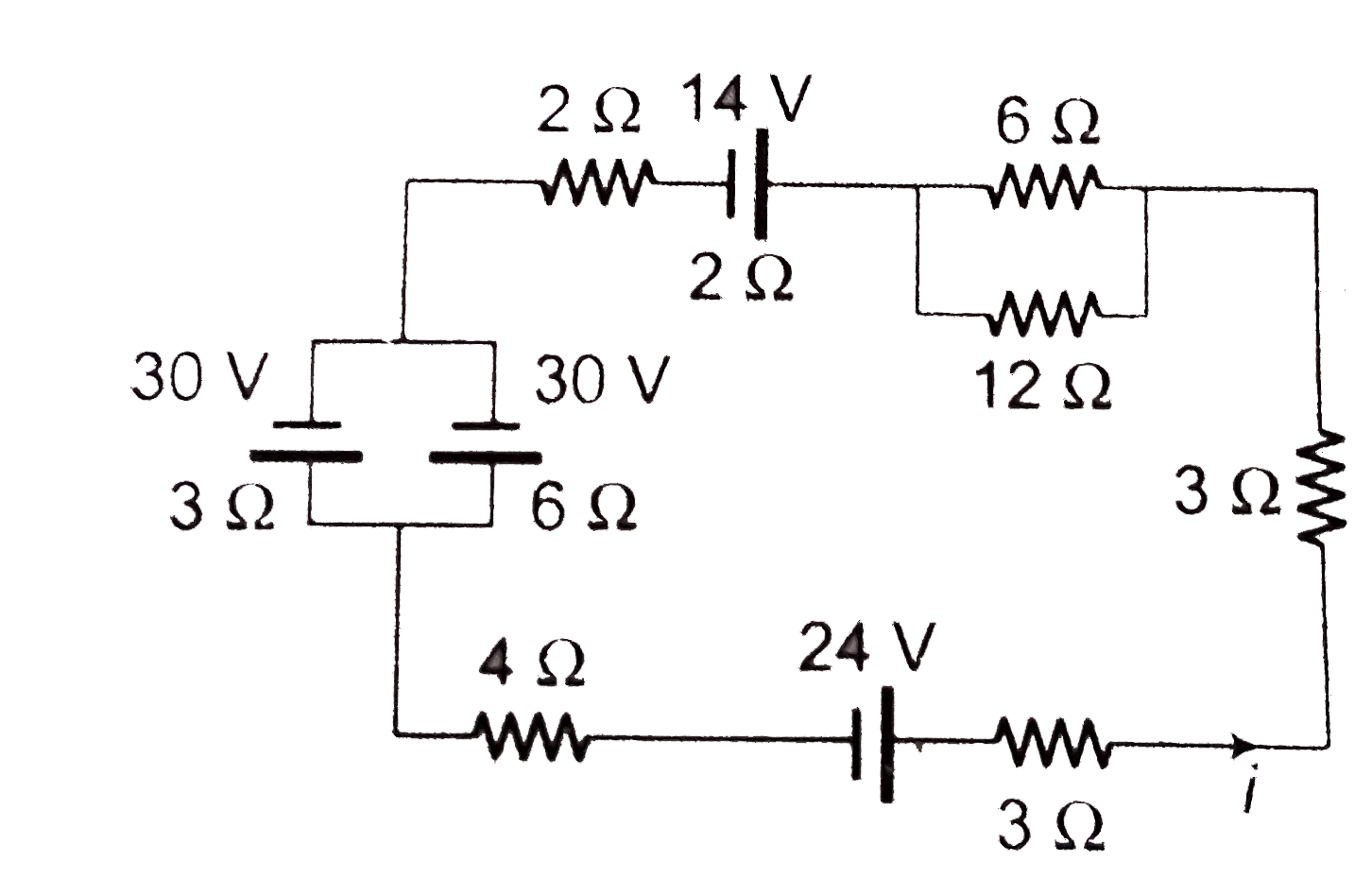
View SolutionFind the position of instantaneous centre of rotation and angular velocity of the disc in the following cases as shown. Radius of disc is R in each case.

View SolutionFind the position of instantaneous centre of rotation and angular velocity of the disc in the following cases as shown. Radius of disc is R in each case.

View SolutionFind the equivalent resistance between A and B in the following cases.
(a)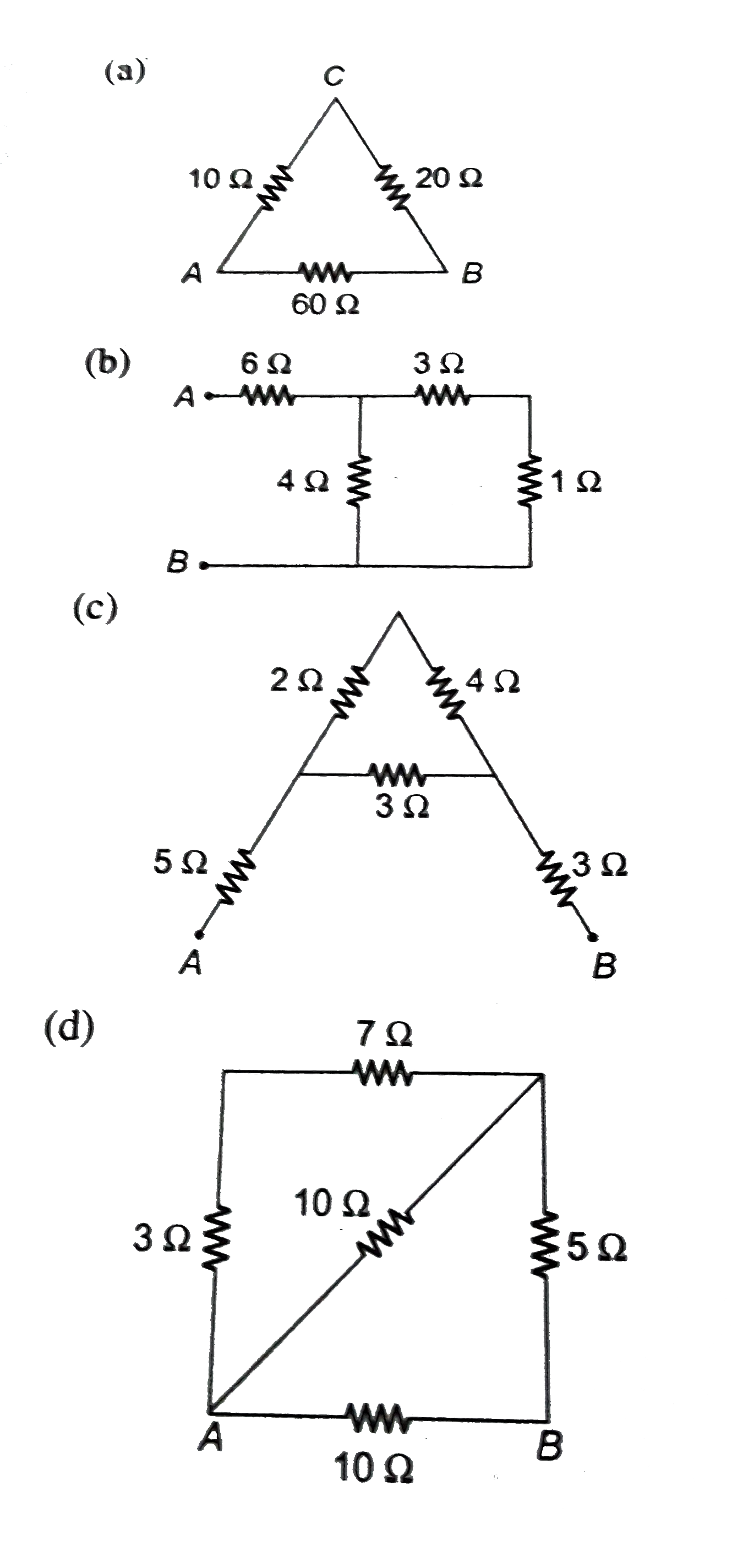 .
.
View SolutionFind the equivalent resistance between A and B in the following cases.
(a)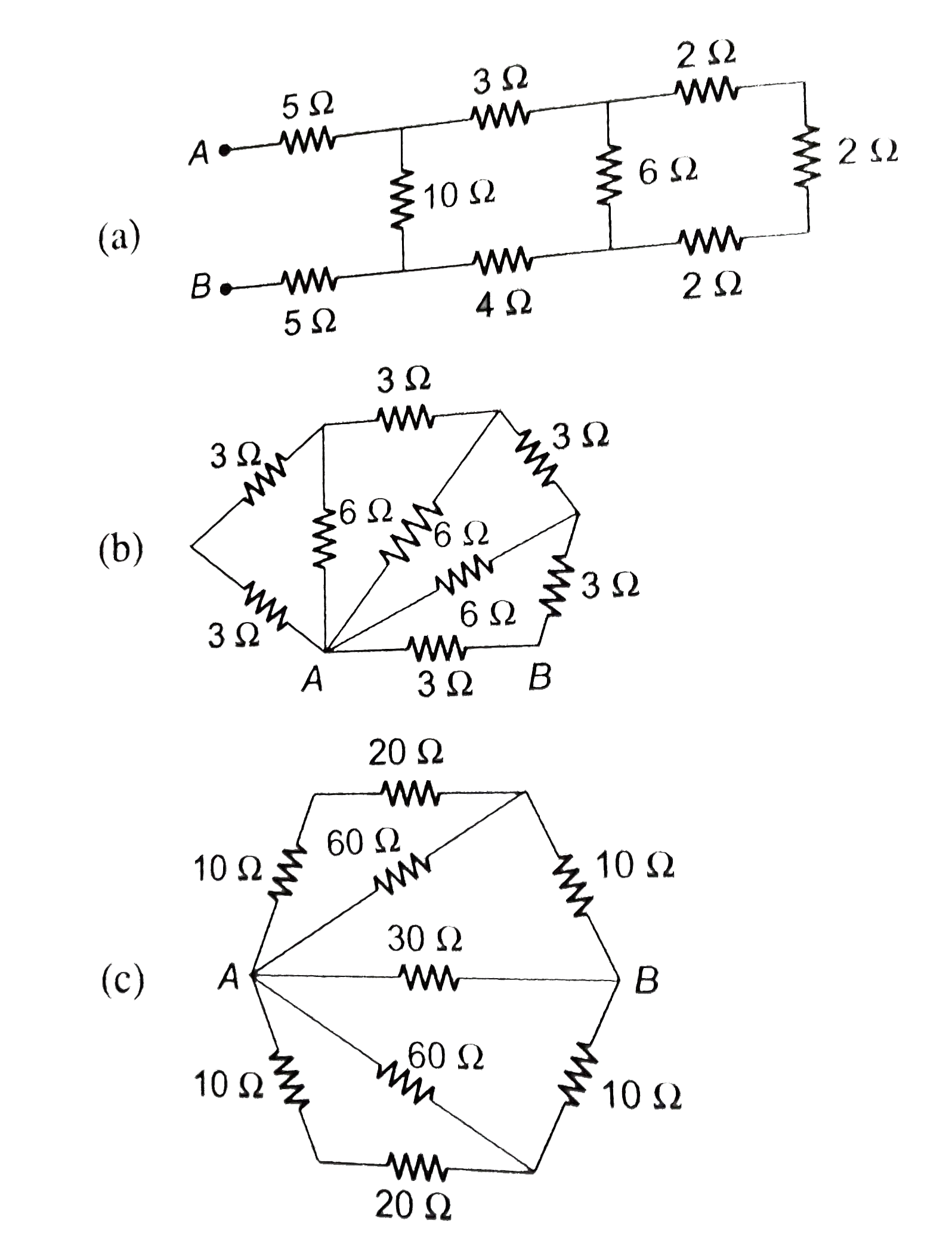 .
.
View SolutionFind the equivalent resistance between A and B in the following cases.
(a) .
.
View SolutionFind the equivalent resistance between A and B in the following cases.
(a)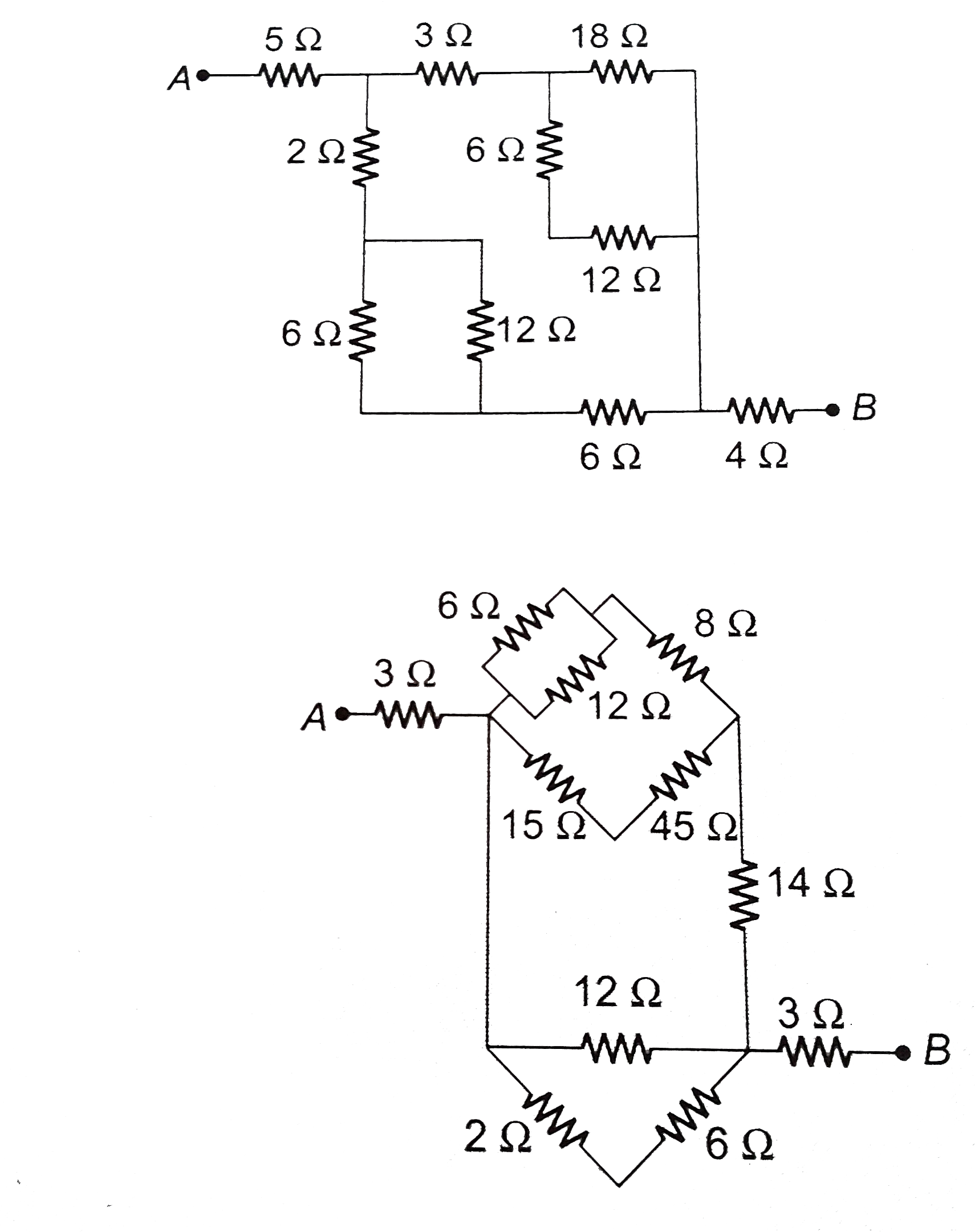 .
.
(b) .
.
View Solution