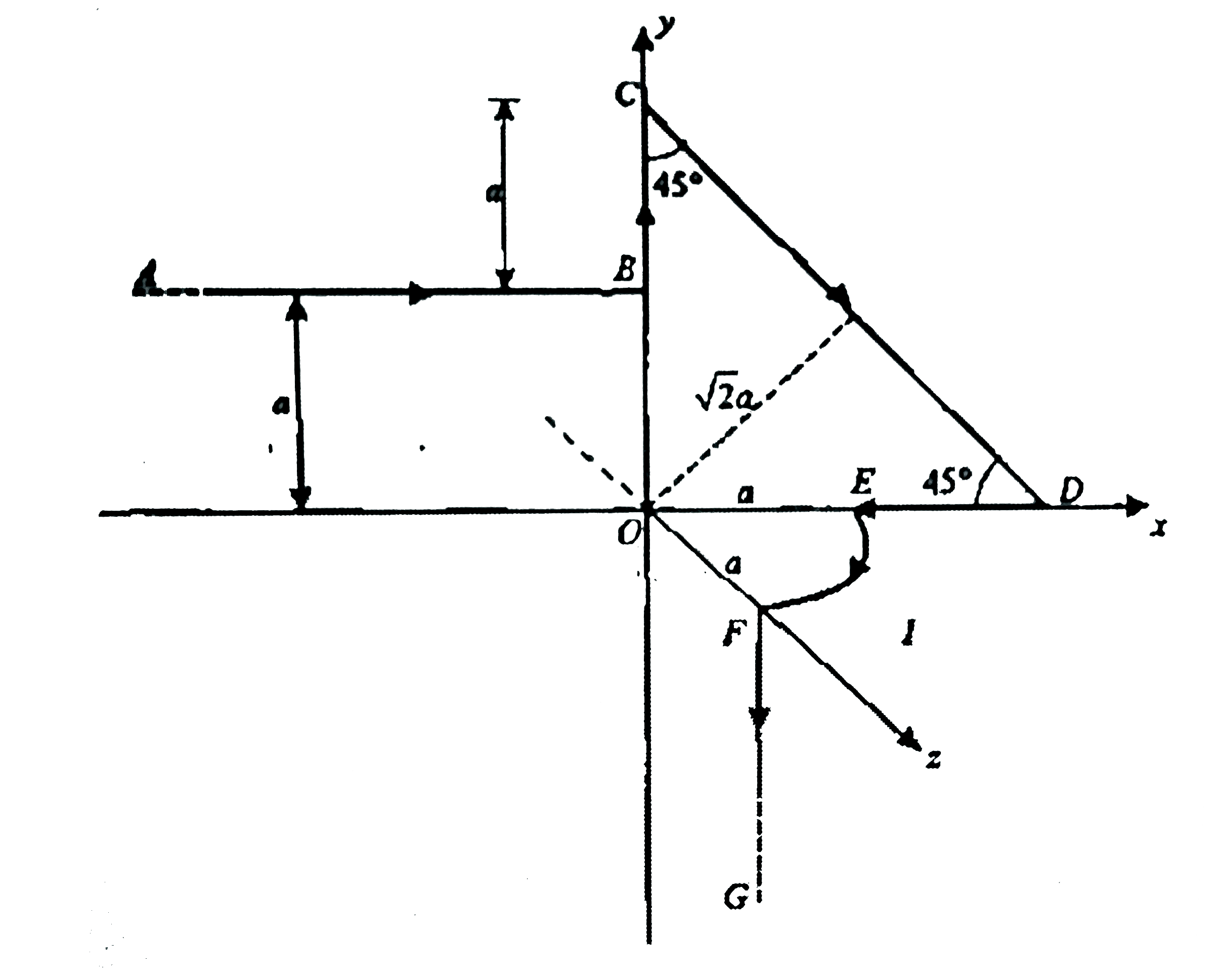
The magnetic field at the origin due to the current flowing in the wire is

A
−μ0I8πa(ˆi+ˆk)
B
μ0I2πa(ˆi+ˆk)
C
μ0I8πa(−ˆi+ˆk)
D
μ0I4πa√2(ˆi+ˆk)
Video Solution
Text Solution
The correct Answer is:C
BOD=0
BOB=0
BAB=μ0l4πa√2[cos45∘(−ˆi)−cos45∘ˆk]=μ0I8πa(−ˆi+ˆk)

|
Updated on:21/07/2023
Topper's Solved these Questions
- BOOK - RESONANCECHAPTER - ELECTRODYNAMICSEXERCISE - Exercise-2 PART-226videos
ELECTRODYNAMICS
- BOOK - RESONANCECHAPTER - ELECTRODYNAMICSEXERCISE - Exercise-2 PART-318videos
ELECTRODYNAMICS
- BOOK - RESONANCECHAPTER - ELECTRODYNAMICSEXERCISE - Exercise-1 PART-254videos
ELECTRODYNAMICS
- BOOK - RESONANCECHAPTER - ELECTRO MAGNETIC WAVESEXERCISE - Exercise 327videos
ELECTRO MAGNETIC WAVES
- BOOK - RESONANCECHAPTER - ELECTROMAGNETIC INDUCTIONEXERCISE - A.l.P19videos
ELECTROMAGNETIC INDUCTION
Similar Questions
Knowledge Check
- Question 1 - Select One
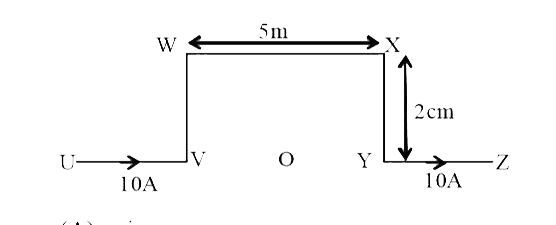
The resulting magnetic field at the point O due to the current carrying wire shown in the figure:
 APoints out of the pageBpoints into the pageCis zeroDis the same as due to the segment WX along.
APoints out of the pageBpoints into the pageCis zeroDis the same as due to the segment WX along. - Question 2 - Select One
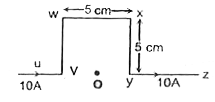
What will be the resulatant field at the origin due to the four indinite length wires if each wire produces magnetic field B at origin ?
 A4BB√2BC2√2BDZero
A4BB√2BC2√2BDZero - Question 3 - Select One
Magnetic field produced at the point O due to current flowing in an infinite wire shaped as shown in the figure is
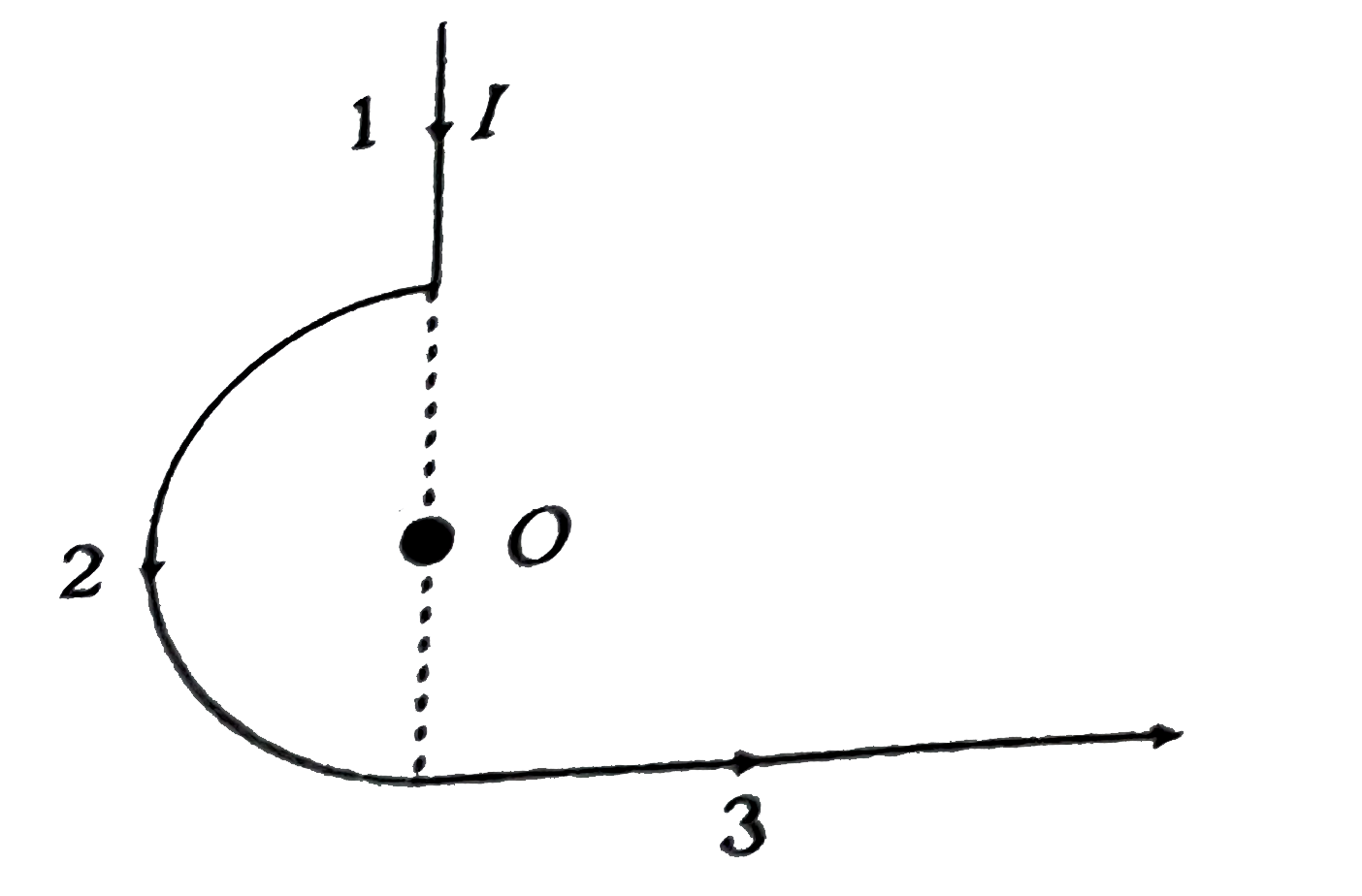 Aμ0I4πRBμ0I4R−μ0I4πRCμ0I4R−μ0I2πRDμ0I4R+μ0I4πR
Aμ0I4πRBμ0I4R−μ0I4πRCμ0I4R−μ0I2πRDμ0I4R+μ0I4πR
Find the magnetic field at the origin due to the combination of two semi infinite wires and a semicircular wire as shown.
 View Solution
View SolutionThe intensity of magnetic field at any point produced by a current flowing through a wire, is dependent on the ............
View SolutionFind the magnitude and direction of magnetic field at point P due to the current carrying wire as shown in
 View Solution
View SolutionFind the magnetic induction vector at origin O due to the current carrying wire configuration as shown in figure-4.33.
 View Solution
View SolutionThe magnetic field at O due to current in the infinite wire forming a loop as a shown in Fig.
 View Solution
View Solution