The current density $\bar{J}$ inside a long, solid cylindrical wire of radius $a = 12 m m$ is in the direction of the central axis, and its magnitude varies linearly with radial distance r from the axis according to $J = \frac{J_{0} r}{a}$ , where $J_{0} = \frac{10^{5}}{4 π} A / m^{2}$ . Find the magnitude of the magnetic field at $r = \frac{a}{2}$ in $μ T$

Video Solution

Text Solution

Verified by Experts

The correct Answer is: $10$

Current in the element $= J (2 π r . d r)$
Current enclosed by Amperian loop of radius $\frac{a}{2}$
$l = \underset{0}{\int^{a / 2}} \frac{J_{0} r}{a} .2 π r . d r = \frac{2 π J_{0}}{3 a} {(\frac{a}{2})}^{3} = \frac{π J_{0} a^{2}}{12}$
Applying Ampere's law
$B .2 π . \frac{a}{2} = μ_{0} . \frac{π J_{0} a^{2}}{12} \Rightarrow B = \frac{μ_{0} J_{0} a}{12}$
On putting values
$B = 10 μ T$

|

Updated on:21/07/2023

Class 12 PHYSICS ELECTROMAGNETIC INDUCTION

Topper's Solved these Questions

Similar Questions

Knowledge Check

Question 1 - Select One
For a long cylindrical wire of radius a=12 mm, we know that its current density $\to J$ is along the direction of the central axis and its magnitude varies linearly with radial distance r from the axis according to the relation $J = \frac{J_{0} r}{a}$ , where $J_{0} = \frac{10^{5}}{4 π} A / m^{2}$ . Calculate the magnitude of the magnetic induction at a position $r = \frac{a}{2}$ (in $μ T$ )
A10
B20
C30
D40
Question 2 - Select One
A current i is uniformly distributed over the cross section of a long hollow cylinderical wire of inner radius $R_{1}$ and outer radius $R_{2}$ . Magnetic field B varies with distance r form the axis of the cylinder is
A
B
C
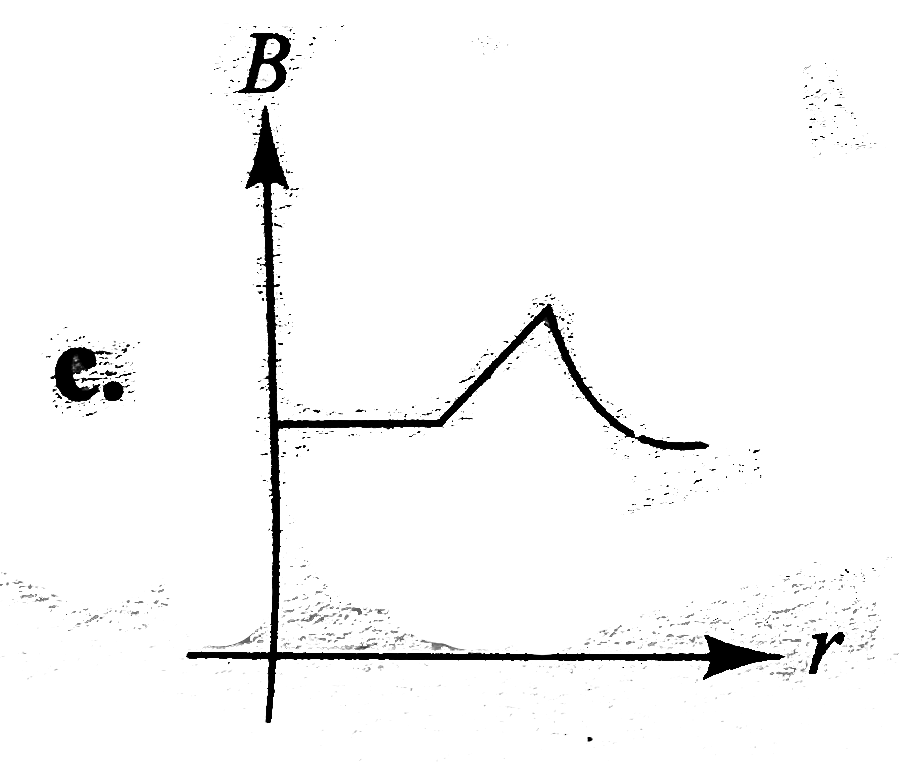D
Question 3 - Select One
The current density is a solid cylindrical wire a radius R, as a function of radial distance r is given by $J (r) = J_{0} (1 - \frac{r}{R})$ . The total current in the radial regon r = 0 to $r = \frac{R}{4}$ will be :
A $\frac{5 J_{0} π R^{2}}{32}$
B $\frac{5 J_{0} π R^{2}}{96}$
C $\frac{3 J_{0} π R^{2}}{64}$
D $\frac{J_{0} π R^{3}}{128}$

RESONANCE-ELECTRODYNAMICS-Advanced level problems

Home
Ask Doubt
Profile