In the figure shown a positively charged particle of charge q and mass m enters into a uniform magnetic field of strength B as shown in the figure.The magnetic field points inwards and is present only within a region of width d.The initial velocity of the particle is perpendicular to the magnetic field and ϕ=30∘.Find the time spent by the particle inside the magnetic field if d=0.2m,B=1T,q=1C,m=1kg and v=1m/s.Use sin45∘=0.7 if required .

The correct Answer is:π12sec.
As the particle enters the region of magnetic field, it moves in a circular path of radius R=mvqB=1m whose centre is at O.and ω=qBm=1rad/sec.
we assumed d to be sufficiently large so that the particle emerges out of region of magnetic field at Q figure −(a).
∴x=R−Rcos60∘=0.5>d
∴ The charge will cross the field and emerge from the right side.
∴ The trajectory of the particle in the region of magnetic field is as shown in figure −b
In the figure (b)PQ is the chord and OC is ⊥ bisector of line PQ.Q is the point from where the particle emerges out.We can see from the geometry that ∠APQ=ϕ+θ2
PQ=dsec(ϕ+θ2)=2Rsinθ2
⇒d=2Rsinθ2cos(ϕ+θ2)=R[sin(θ2+ϕ+θ2)+sin(−ϕ)]
⇒d=R[sin(θ+ϕ)−sinϕ]⇒sin(θ+ϕ)=d15+sinθ=0.7
⇒θ+ϕ=45∘⇒t=π12sec.

Topper's Solved these Questions
Similar Questions
A positive charge particle of charge q, mass m enters into a uniform magnetic field with velocity v as shown in the figure. There is no magnetic field to the left of PQ. Find
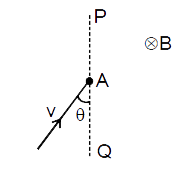
time spent
View SolutionA positive charge particle of charge q, mass m enters into a uniform magnetic field with velocity v as shown in the figure. There is no magnetic field to the left of PQ. Find
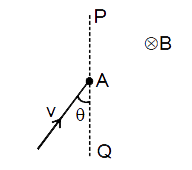
impulse of magnetic force.
View Solution
Knowledge Check
A charged particle of charge q and mass m is shot into a uniform magnetic field of induction B at an angle θ with the field. The frequency of revolution of the particle
ADepends on the angle θBIs independent of the angle θCIs proportional to the specific charge q/m of the particleDIs inversely proportional to the value of BIf a charged particle of charge to mass ratio (qm)=α centers in a magnetic field of strength B at a speed v=(2αd)(B), then
 Aangle subtended by the path of charged particle in magnetic field at the centre of circular path is 2πBThe charge will move on a circular path and then will come out from magnetic field at some distance from the point of indertionCThe time for which particle will be in the magnetic field is 2παBDAngle subtended by the path of charged particle in magnetic field at the centre of circular path is π/2
Aangle subtended by the path of charged particle in magnetic field at the centre of circular path is 2πBThe charge will move on a circular path and then will come out from magnetic field at some distance from the point of indertionCThe time for which particle will be in the magnetic field is 2παBDAngle subtended by the path of charged particle in magnetic field at the centre of circular path is π/2
A positive charge particle of charge q, mass m enters into a uniform magnetic field with velocity v as shown in the figure. There is no magnetic field to the left of PQ. Find

distance travelled in the magnetic field
View SolutionA charge particle of mass m and charge q enters in a region of uniform magnetic field as shown in figure.The magnitude of change in linear momentum due to magnetic field will be
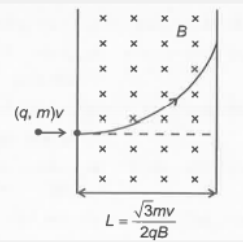
View SolutionA positive charge particle of charge q and mass m enters into a uniform magnetic field with velocity v as shown in Fig. There is no magnetic field to the left of PQ. Find (a) time spent, (b) distance travelled in the magnetic field, (c) impulse of magnetic force.

View SolutionA positive charge particle of charge q and mass m enters into a uniform magnetic field with velocity v as shown in Fig. There is no magnetic field to the left of PQ. Find (a) time spent, (b) distance travelled in the magnetic field, (c) impulse of magnetic force.

View SolutionA positive charge particle of charge q and mass m enters into a uniform magnetic field with velocity v as shown in Fig. There is no magnetic field to the left of PQ. Find (a) time spent, (b) distance travelled in the magnetic field, (c) impulse of magnetic force.

View SolutionA positive charge particle of charge q, mass m enters into a uniform magnetic field with velocity v as shown in the figure . There is no magnetic field to the left of PQ . Find (i) time spent,

(ii) distance travelled in the magnetic field
(iii) inpulse of magnetic force.
View Solution
