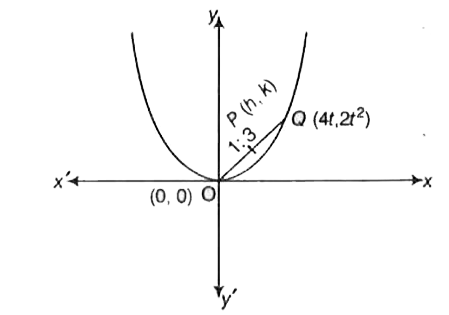
माना O शीर्ष तथा Q परवलय: x2=8y पर स्थित कोई बिन्दु है। यदि बिन्दु P, रेखाखण्ड QQ को अन्तः 1: 3 के अनुपात में विभाजित करता है, तब P का बिन्दुपथ होगा
x2=y
y2=x
y2=2x
x2=2y
The correct Answer is:D
परवलय x2=8y पर कोई बिंदु (4t,2t2) है। बिंदु P, बिन्दुओ O(0,0) तथा Q(4t,2t2) को मिलाने वाले रेखाखण्ड को 1:3 के अनुपात में विभाजित करता है। इशलिये अंत: विभाजन का सूत्र प्रयोग कीजिये। परवलय का समीकरण निम्न है
x2=8y........(i)
माना परवलय (i) पर कोई बिंदु Q(4t,2t2) है।
माना P(h,k) बिन्दुओ (0,0) तथा (4t,2t2) को मिलाने वाले रेखाखण्ड को 1:3 के अनुपात में विभाजित करता है
∴h=1×4t+3×04
⇒h=t
तथा k=1×2t2+3×04
⇒k=t22
⇒k=12h2
⇒2k=h2
⇒2y=x2, जोकि अभीष्ट बिन्दुपथ है
Topper's Solved these Questions
- BOOK - JEE Main & Advanced (Hindi Medium)CHAPTER - परवलयEXERCISE - बहुविकल्पीय प्रश्न II7videos
परवलय
- BOOK - JEE Main & Advanced (Hindi Medium)CHAPTER - परवलयEXERCISE - रिक्त स्थानों की पूर्ति कीजिये1videos
परवलय
- BOOK - JEE Main & Advanced (Hindi Medium)CHAPTER - निश्चित समाकलन EXERCISE - एकल पूर्णाक प्रश्न7videos
निश्चित समाकलन
- BOOK - JEE Main & Advanced (Hindi Medium)CHAPTER - प्रतिलोम वृत्तीय फलन EXERCISE - एकल पूर्णांक प्रश्न1videos
प्रतिलोम वृत्तीय फलन
Similar Questions
परवलयों y=x2 तथा y=−x2+4x−4 की उभयनिष्ठ स्पर्शी का समीकरण है।
04:29View Solutionपरवलय y2=4x के नाभिलम्ब (latusrectum) के सिरों पर खींची गयी स्पर्शी का प्रतिछेद बिंदु .............है
03:08View Solutionदिया है कि किसी वास्तविक संख्या x के लिए [x], अधिकतम पूर्णांक को दर्शाता है यदि अन्तराल [−10,10] पर वास्तविक मानों वाला फलन f निम्न प्रकार से परिभाषित है f(x)={x−[x],if [x] is Odd,1+[x]−x, if [x] is Even तो π210∫10−10f(x)cosπxdx का मान है
02:37View Solutionमाना f:[0,4π]→[0,π],f(x)=cos−1(cosx) के द्वारा परिभाषित है। तब x∈[0,4π] में समीकरण f(x)=10−x10 को संतुष्ट करने वाले बिंदुओं की संख्या है
02:54View Solutionपरवलय y2=4ax की नाभि तथा उस पर स्थित चर को मिलाने वाले रेखाखण्ड के मध्य - बिंदु का पथ एक परवलय है जिसकी नियता है :
03:57View Solutionएक सरल रेखा द्वारा अक्षो के बीच काटे गये अन्तः खण्ड को बिंदु (7,9),3:1 के अनुपात में अन्तः विभाजित करता है रेखा का समीकरण ज्ञात कीजिए
03:38View Solutionमाना A(2,−3) तथा B(−2,1) एक त्रिभुज ABC के शीर्ष है । यदि इस त्रिभुज का केन्द्रक सरल रेखा 2x+3y=1पर भ्रमण करता है तो शीर्ष C का बिन्दुपथ है -
02:19View Solutionयदि बिंदु A जिसका स्थिति सदिश ¯a+2¯b है तथा सदिश ¯a,AB को 2:3 के अनुपात में विभाजित करता है तो B का स्थिति सदिश है:
02:15View Solutionएक सरल रेखा बिन्दु (-1,5) से होकर जाती है और रेखा द्वारा अक्षो के बीच काटे हुए भाग को यह बिन्दु 3:2 के अनुपात में विभाजित करता है। रेखा का समीकरण ज्ञात कीजिए|
03:36View Solutionमाना कि परवलय x2=8y का शीर्ष O तथा उस पर बिंदु Q है। यदि बिंदु P रेखाखण्ड OQ को 1:3 के आन्तरिक अनुपात में विभाजित करता है, तो P का बिन्दुपथ है :
05:05View Solutionयदि आरगंड आरेख पर बिन्दु P सम्मिश्र संख्या z = x + iy को निरूपित करता है, तो P का बिन्दुपथ ज्ञात कीजिए जबकि कोणांक (z) = 0
03:50View Solutionयदि आरगंड आरेख पर बिन्दु P सम्मिश्र संख्या z = x + iy को निरूपित करता है, तो P का बिन्दुपथ ज्ञात कीजिए जबकि arg(z−2−3i)=π4
04:29View Solutionयदि आरगंड आरेख पर बिन्दु P सम्मिश्र संख्या z = x + iy को निरूपित करता है, तो P का बिन्दुपथ ज्ञात कीजिए जबकि ∣∣∣z−2z+2∣∣∣=5
07:49View Solutionमाना एक ऊर्ध्वाधर मीनार AB ऐसी है कि उसका सिरा A भूमि पर है। माना AB का मध्य-बिन्दु C है और भूमि पर स्थित बिन्दु P ऐसा है कि AP=2AB यदि ∠BPC=β है, तो tanβ बराबर है
05:40View Solutionयदि एक त्रिभुज , जिसका एक शीर्ष परवलय के शीर्ष परवलय y2+4(x−a2)=0 तथा अन्य दोनों शीर्ष y-अक्ष तथा परवलय के प्रतिच्छेदन बिंदुओं पर हैं , का क्षेत्रफल 250 वर्ग इकाई है , तो 'a' का एक मान है
02:06View Solutionयदि एक अतिपरवलय के शीर्ष (−2,0) तथा (2,0) पर है तथा इसकी एक नाभि (−3,0) पर है, तो निम्न में से कौन-सा बिन्दु इस अतिपरवलय पर स्थित नहीं है
05:00View Solution

