उन वृत्तों के केन्द्र, जो वृत्त को बाह्य रूप से स्पर्श करते हैं तथा.X-अक्ष को भी स्पर्श करते हैं, स्थित हैं
एक वृत्त पर
एक दीर्घवृत पर जो वृत्त नहीं है
एक अतिपरवलय पर
एक परवलय पर
The correct Answer is:D
दिया है, वृत्त का समीकरण जिसका केंद्र C(4,4) तथा त्रिज्या
माना आव्यश्यक वृत्त का केंद्र चुकी वह यह X -अक्ष को स्पर्श करती है अंत: इसकी =|y| त्रिज्या तथा यह भी दिया गया है की वृत्त जिसका केंद्र है वृत्त को भी स्पर्श करती है इसलिए
स्थिति I यदि तब
जोकि एक परवलय का समीकरण है
स्थिति I यदि तब
यह भी एक परवलय का समीकरण है
Topper's Solved these Questions
- परवलयBook:JEE Main & Advanced (Hindi Medium)Chapter:परवलयExercise:बहुविकल्पीय प्रश्न II
Explore 7 Videos
- परवलयBook:JEE Main & Advanced (Hindi Medium)Chapter:परवलयExercise:रिक्त स्थानों की पूर्ति कीजिये
Explore 1 Video
- निश्चित समाकलन Book:JEE Main & Advanced (Hindi Medium)Chapter:निश्चित समाकलन Exercise:एकल पूर्णाक प्रश्न
Explore 7 Videos
- प्रतिलोम वृत्तीय फलन Book:JEE Main & Advanced (Hindi Medium)Chapter:प्रतिलोम वृत्तीय फलन Exercise:एकल पूर्णांक प्रश्न
Explore 1 Video
Similar Questions
परवलयों y=x2 तथा y=−x2+4x−4 की उभयनिष्ठ स्पर्शी का समीकरण है।
View Solutionपरवलय y2=4x के नाभिलम्ब (latusrectum) के सिरों पर खींची गयी स्पर्शी का प्रतिछेद बिंदु .............है
View Solutionदिया है कि किसी वास्तविक संख्या x के लिए [x], अधिकतम पूर्णांक को दर्शाता है यदि अन्तराल [−10,10] पर वास्तविक मानों वाला फलन f निम्न प्रकार से परिभाषित है f(x)={x−[x],if [x] is Odd,1+[x]−x, if [x] is Even तो π210∫10−10f(x)cosπxdx का मान है
View Solutionमाना f:[0,4π]→[0,π],f(x)=cos−1(cosx) के द्वारा परिभाषित है। तब x∈[0,4π] में समीकरण f(x)=10−x10 को संतुष्ट करने वाले बिंदुओं की संख्या है
View Solutionयदि वृत्त x2+y2=a2 तथा x2+y2−6x−8y+9=0 एक दूसरे को बहिगर्त स्पर्श करते है तो a =
View Solutionदो वृत्त एक -दूसरे को अन्तः स्पर्श करते है ,तो उनकी उभयनिष्ठ स्पर्श रेखाओ कि संख्या लिखिए।
View Solutionदो वृत्त एक दूसरे को अन्तः स्पर्श करते है ,तो उनकी उभयनिष्ठ स्पर्श रेखाओ की संख्या लिखिये।
View Solutionदीर्घवृत्त 9x2+5y2−30y=0 के दीर्घ अक्ष के सिरों पर खींची गई स्पर्श रेखाओं के समीकरण हैं
View Solutionखण्ड 'अ'खण्ड 'ब'1.वृत्त के अन्तः बिंदु से खींची गयी स्पर्श रेखाओं की संख्या(a)समकोण2.वृत्त के किसी बिंदु से खींची गयी स्पर्श रेखाओं की संख्या(b)स्पर्श रेखा3.वृत्त के बाह्य बिंदु से वृत्त पर खींची गयी स्पर्श रेखाओं की संख्या(c)शून्य4.स्पर्श रेखा और स्पर्श बिंदु से जाने वाली त्रिज्या के बीच बना कोण(d)एक5.वृत्त को केवल एक बिंदु पर प्रतिच्छेद करने वाली रेखा(e)दो
View Solutionआकृति में, वृत्त के छायांकित भाग को कहते हैं:
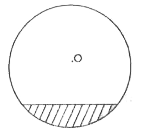
View Solutionउन परिमेय संख्याओं के दशमलव प्रसारों को लिखिए जो सांत हैं।
41124
View SolutionTwo circles of radii 8 cm and 6 cm touch each other externally. The length of the direct common tangent is: 8 सेमी तथा 6 सेमी त्रिज्याओं वाले दो वृत्त एक-दूसरे को बाहर से स्पर्श करते हैं | प्रत्यक्ष उभयनिष्ठ स्पर्श रेखा की लंबाई कितनी है ?
View Solutionदाँत और जीभ के स्पर्श से बोले जाने वाले वर्ण को क्या कहते हैं?
View Solutionनाइट्रोजन (III) के व्युत्पन्न किस रूप में कार्य करते हैं?
View Solutionआप PbCrO_4 के गुणों को कैसे वर्णित करते हैं?
View Solutionएक धनायन केंद्र में है जो तीन ऋणायन को स्पर्श करता है। मान लीजिए कि ऋणायन भी एक दूसरे को स्पर्श करते हैं। सीमांत त्रिज्या अनुपात, r^(+)//r^(-) है:
View Solution