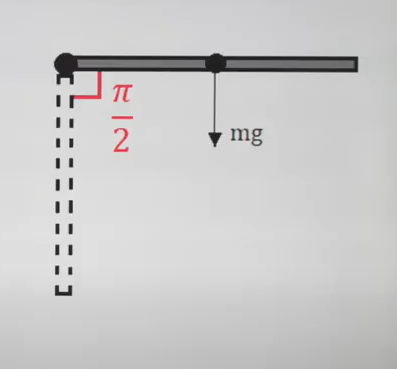
A bead is contrained to move on rod in granvity free space as shown in figure. The rod rotating with ,angular velocity and angulnr acceleration α about its end. If μ is coefficient of friction. Mark the correct option. ( Rod rotates in the plane of paper.)
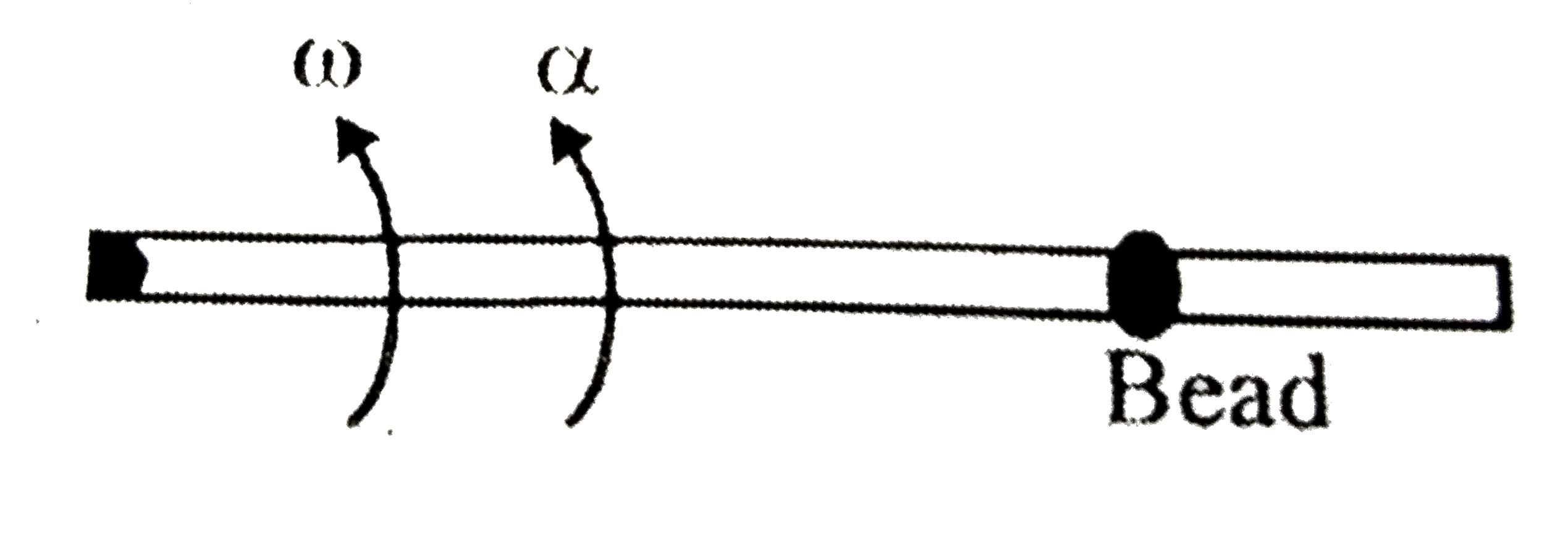
If μ=ω2α friction ion on bead is static in nature
If μ≥ω2α friction on bead is kinetic in nature
If μ≤ω2α friction is static
If bead does not slide relative to rod. Friction will not exist between bead and rod.
The correct Answer is:A
Step by step video, text & image solution for A bead is contrained to move on rod in granvity free space as shown in figure. The rod rotating with ,angular velocity and angulnr acceleration alpha about its end. If mu is coefficient of friction. Mark the correct option. ( Rod rotates in the plane of paper.) by Physics experts to help you in doubts & scoring excellent marks in Class 12 exams.
Topper's Solved these Questions
- BOOK - ALLENCHAPTER - CIRCULAR MOTIONEXERCISE - MCQ14videos
CIRCULAR MOTION
- BOOK - ALLENCHAPTER - CIRCULAR MOTIONEXERCISE - EXERCISE (J-M)5videos
CIRCULAR MOTION
- BOOK - ALLENCHAPTER - CIRCULAR MOTIONEXERCISE - Martrix match1videos
CIRCULAR MOTION
- BOOK - ALLENCHAPTER - BASIC MATHSEXERCISE - Question1videos
BASIC MATHS
- BOOK - ALLENCHAPTER - CURRENT ELECTRICITYEXERCISE - All Questions427videos
CURRENT ELECTRICITY
Similar Questions
Knowledge Check
- Question 1 - Select One
A rod is rotating with angular velocity ω about axis AB. Find cosθ.
 Ag2lω2Bglω2C2g(lω)2D3g2lω2
Ag2lω2Bglω2C2g(lω)2D3g2lω2 - Question 2 - Select One
A rod AB is placed on smooth inclined plane as shown in the figure. At the instant which is shown in the figure, the angular velocity of the rod is
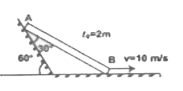 A8 rad /sB5 m/sC15 rad/sDnone
A8 rad /sB5 m/sC15 rad/sDnone - Question 3 - Select One
A long horizontal rod has a bead which can slide along its length and is initially placed at a distance L from one end A of the rod. The rod is set in angular motion about A with a constant angular acceleration, α. If the coefficient of friction between the rod and bead is μ, and gravity is neglected, then the time after which the bead starts slipping is :
A√μαBμ√αC1√μαDinfinitesimal
A long horizontal rod has a bead which can slide along its length and initially placed at a

distance L from one end A of the rod. The rod is set in angular motion about A with constant angular acceleration α. if the coefficient of friction between the rod and the bead is μ, and gravity is neglected, then the time after which the bead starts slipping isView SolutionA long horizontal rod has a bead which can slide along its length and initially placed at a

distance L from one end A of the rod. The rod is set in angular motion about A with constant angular acceleration α. if the coefficient of friction between the rod and the bead is μ, and gravity is neglected, then the time after which the bead starts slipping isView SolutionA long horizontal rod has a bead which can slide along its length and initially placed at a

distance L from one end A of the rod. The rod is set in angular motion about A with constant angular acceleration α. if the coefficient of friction between the rod and the bead is μ, and gravity is neglected, then the time after which the bead starts slipping isView SolutionA rod is hinged (free to rotate) ast its centre O as shown in figue. Two point charge +q and +q are kept at its two ends. Rod is placed in uniform electric field E as shown. Space is gravity free. Choose the correct options.
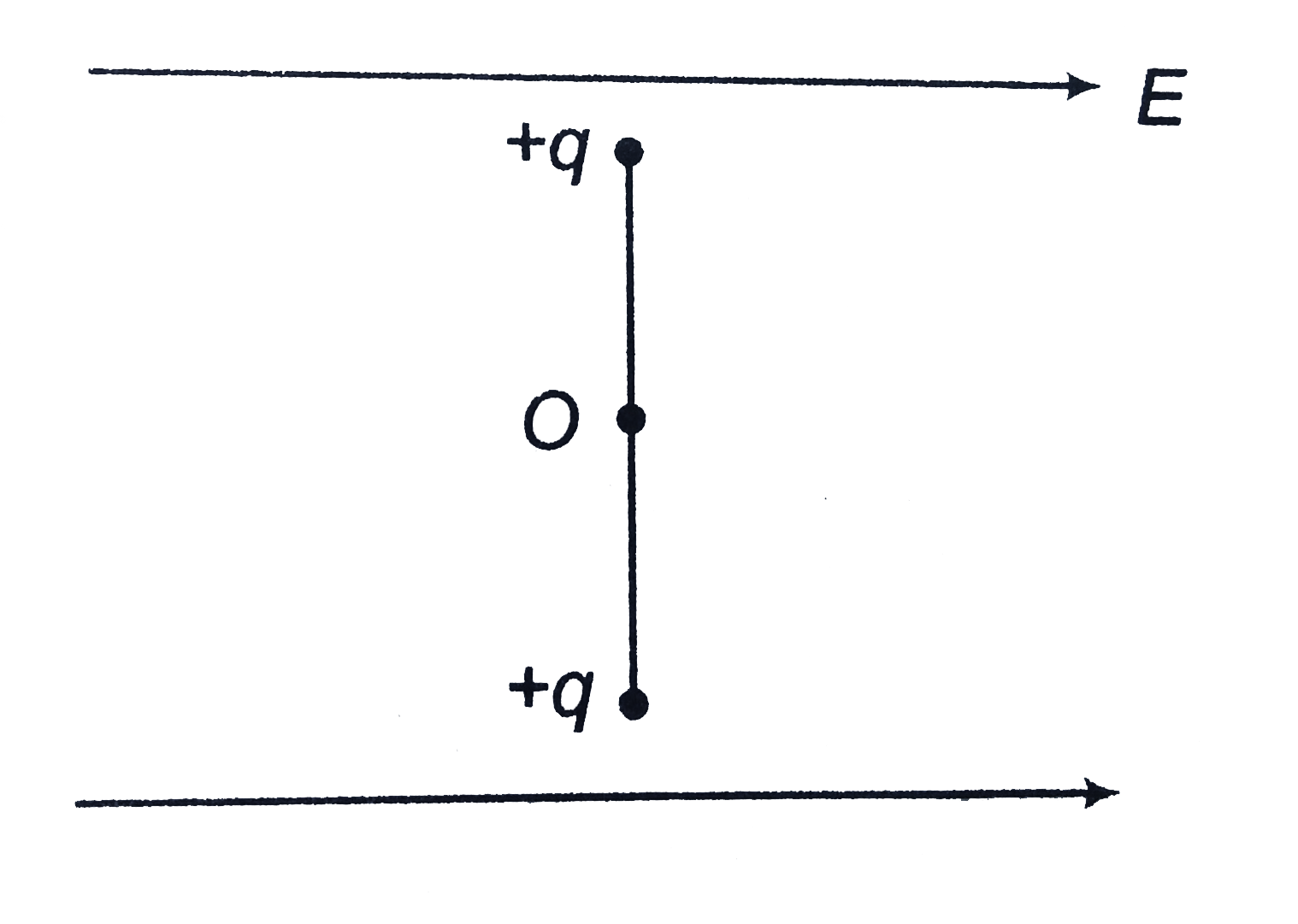 View Solution
View SolutionA charged rod having charge as shown is rotating with angular velocity omega about on hinge at its centre. At the instant shown rod is along x- axis Consider effect of field at the instant shown.
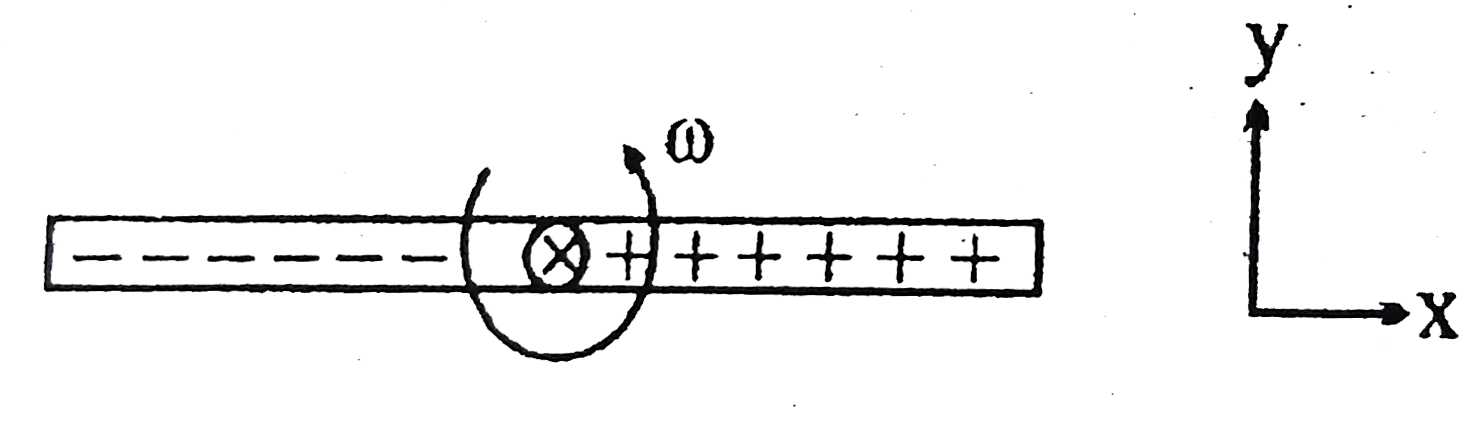 View Solution
View Solution